どうも、木村(@kimu3_slime)です。
高校数学では、対数関数について学びます。対数関数の応用のひとつとして、対数スケールを紹介していきましょう。
高校生物では、ある生物の種において、個体数と相対年齢の関係をグラフにしたもの、生存曲線を学びます。
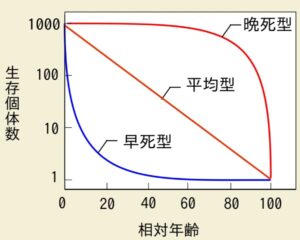
画像引用:高等学校生物/生物II/個体群と生物群集 – Wikibooks
晩死型は人間、平均型は鳥、早死型は木などが当てはまります。
この生存曲線の図では、縦軸は\(100,200,300\)のように等間隔ではなく、\(1,10,100,1000\)と1目盛り毎に10倍になっています。このような尺度を対数スケール、ログスケールと呼びます。
特に今回は、横軸は通常のスケール(線形スケール)で縦軸が対数スケールなので、片対数グラフとも呼ばれます。両軸が対数スケールのときは、両対数グラフです。
対数スケールでは何が起こっているか、数式の上で考えてみましょう。
最もわかりやすいのは、平均型です。10の「何乗か」という部分が、一定のペースで減っていきます。
つまり、
\[g(x) = 10^{-\frac{3}{100}x+3}\]
という関係がもともとあるとき、それを対数スケール(常用対数)でグラフにすれば、
\[\log_{10} g(x) = -\frac{3}{100} x+3\]
と直線(1次関数)になります。
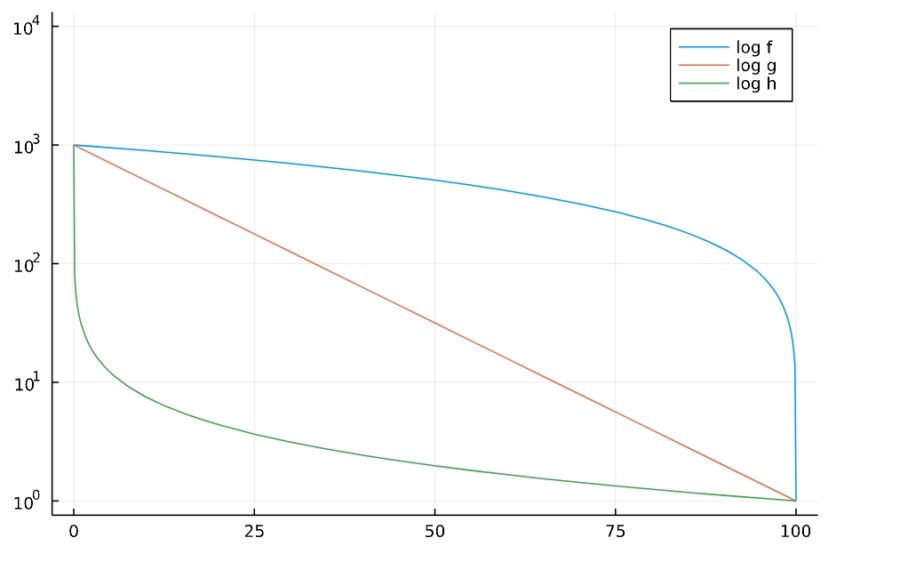
このように、「10の何乗か」で変化を捉えるときには、対数スケールがグラフをシンプルにしてくれます。
上の図で用いた晩死型、早死型のグラフは
\[f(x) = 10^{ \frac{3}{100^{0.15}}(-x+100)^{0.15}}\]
\[h(x) =10^{ -\frac{3}{100^{0.15}}x^{0.15}} \]
です。これは対数を取れば、べき乗関数
\[\log _{10} f(x) = \frac{3}{100^{0.15}}(-x+100)^{0.15} \]
\[\log_{10} h(x) = -\frac{3}{100^{0.15}}x^{0.15} \]
となっています。
もし対数スケールを使わずに相対年齢と個体数の関係をプロットしたら、次のようになります。
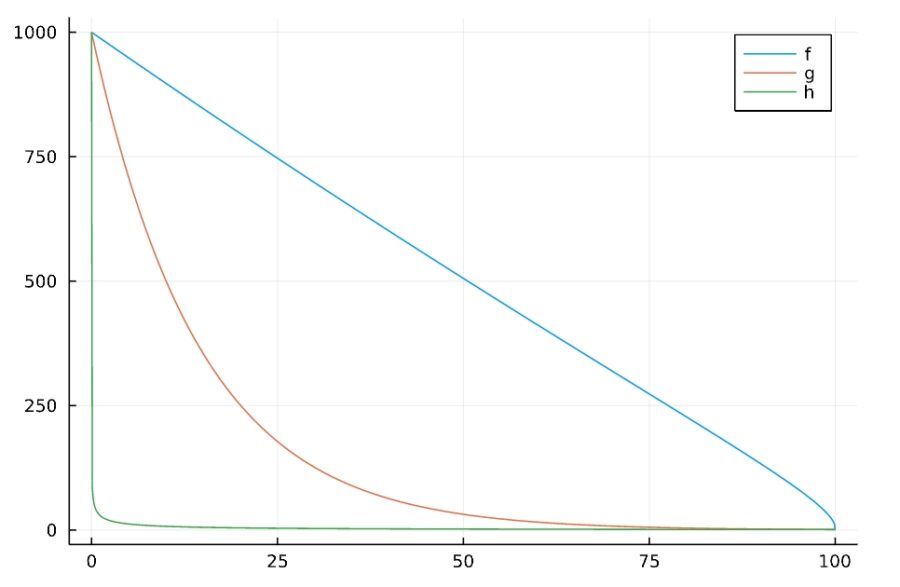
早死型のグラフは急激に減少しているので、変化の具合が読み取りにくいです。平均型のグラフも、一定の期間で個体数は1/10になっているのに、そのことはわかりにくいですね。
このように、指数関数的に減少・増加する現象を調べるときには、対数スケールが有効です。
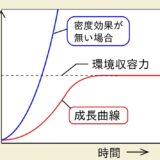
話を変えて、微生物が増殖していくときの個体数のグラフ、マルサスモデルの生存曲線を描くときにも、対数スケールが有効です。
3種の生き物がいたとして、そのまま指数関数的に増加する個体数をグラフにすると、「増加の速さが違う」という漠然とした違いしかわかりません。
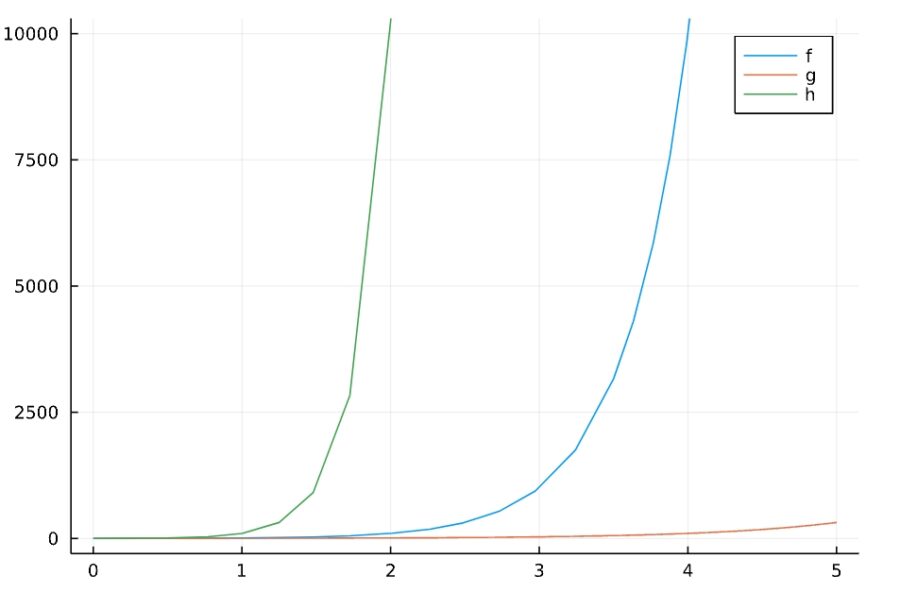
これを対数スケールで描けば、10の「何乗か」が線形的に増えているのがわかりますね。
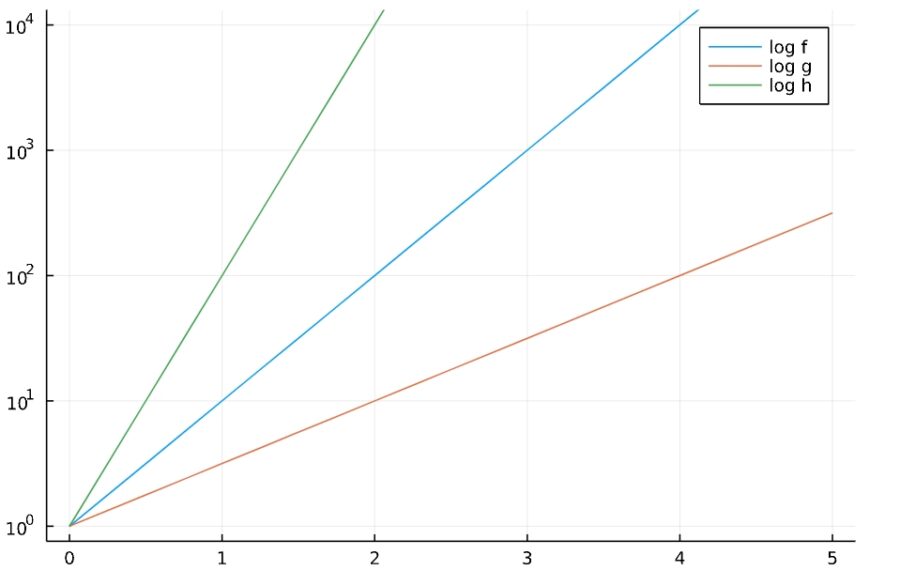
以上、対数をなぜ学ぶかについて、対数スケール、生存曲線を例に紹介してきました。
指数関数的に増加したり減少したりする現象を調べるときに、そのままの尺度だと変化が大きすぎ・小さすぎて、変化率が捉えにくくなります。そこで対数スケールが役に立つことが伝われば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
改訂版 日本一詳しい 大学入試完全網羅 生物基礎・生物のすべて
KADOKAWA (2019-03-20T00:00:00.000Z)
¥2,574
数研出版 (2017-02-09T00:00:01Z)
¥2,486 (コレクター商品)
共立出版 (1998-03-01T00:00:01Z)
¥8,800 (コレクター商品)
こちらもおすすめ
成長曲線と密度効果:マルサス・ロジスティックモデルによる説明