どうも、木村(@kimu3_slime)です。
今回は、コンデンサーの充電・放電の時間変化について、微分方程式による説明をします。
コンデンサーの充電
コンデンサーの充電や放電について考えましょう。電流、電圧の時間変化は、高校物理の参考書では次のグラフのようになるとされています。

画像引用:実戦物理重要問題集 物理基礎・物理
このグラフはどうやって得たのでしょうか。実はその正体は、指数関数です。
今回は、微分方程式を用いることによって、電流・電圧の時間変化のグラフを説明したいと思います。
まず、充電について考えましょう。
電源による電圧は\(V\)、抵抗による電圧は\(V_R = RI\)、コンデンサーによる電圧は\(V_C = \frac{1}{C} Q\)です。
電圧に関するキルヒホッフの法則(電圧は保存される)より、
\[V_R+ V_C = V\]
\[RI +V_C =V\]
が成り立ちます。
\(I,Q,V\)はともに時間変化する、時間の関数です。コンデンサーを流れる電流\(I(t)\)は、コンデンサの電荷\(Q(t)\)の時間変化率なので(電流の定義)、
\[I = \frac{dQ}{dt} = C \frac{dV_C}{dt}\]
です。これらをまとめれば、
\[R C \frac{dV_C}{dt} + V_C = V\]
となります。これは関数\(V_C (t)\)の微分を含む方程式で、微分方程式と呼ばれるものです。
微分方程式を解き、関数\(V_C (t)\)を求めてみましょう。
この方程式の形は、変数分離形に持ち込んで解くことができます。\(V_C\)に関する項を左辺に集めれば、
\[ \frac{1}{V_C -V} \frac{dV_C}{dt} = – \frac{1}{RC}\]
です。両辺を\(t\)について積分すると、
\[\int _{V_C(0)}^{V_C(t)} \frac{1}{y -V} dy = \int_0 ^t -\frac{1}{RC} ds\]
です。左辺は
\[\int _{V_C(0)}^{V_C(t)} \frac{1}{y -V} dy = \log |V_C(t) -V| -\log|V_C(0)-V|\]
で、右辺は
\[\int_0 ^t -\frac{1}{RC} ds =-\frac{t}{RC} \]
なので、
\[\log \frac{|V_C(t) -V|}{|V_C(0)-V|} = -\frac{t}{RC}\]
\[ \frac{|V_C(t) -V|}{|V_C(0)-V|}= e^{- \frac{t}{RC}}\]
となります。
\(t=0\)のときはコンデンサは充電されていないので、\(Q(0)=V_C(0)=0\)です。また、電源の電圧は\(V>0\)です。これらに気をつけて絶対値を外すと、
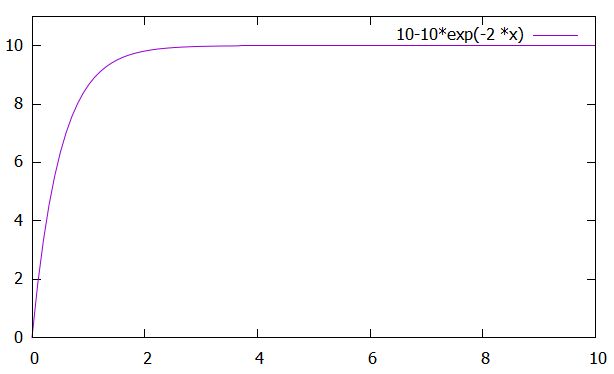
\[\begin{aligned} V_C(t) &= – Ve^{- \frac{t}{RC}} +V\\&= V(1- e^{- \frac{t}{RC}})\end{aligned}\]
と指数関数の形の解を得ることができました。
時間経過すると、指数関数の項は減衰し、
\[\lim_{t\to \infty} V_C(t) = V\]
と電源の電圧に近づいていきます。
電流は、この解の微分によって求めることができます。
\[\begin{aligned} I(t) &= \frac{dQ}{dt}\\& = C \frac{dV_C}{dt} \\&=\frac{V}{RC}e^{-\frac{t}{R}}\end{aligned}\]
これは指数関数的な減衰です。時間経過すると、
\[\lim_{t \to \infty}I(t) =0\]
です。これで充電のグラフについて理解できましたね。
コンデンサーの放電
続いて、コンデンサーの放電について考えましょう。

画像引用:実戦物理重要問題集 物理基礎・物理
さきほどと同じ流れです。
電源による電圧は\(0\)となり、抵抗による電圧は\(V_R = RI\)、コンデンサーによる電圧は\(V_C = \frac{1}{C} Q\)となりました。
電圧に関するキルヒホッフの法則(電圧は保存される)より、
\[V_R+ V_C = 0\]
\[RC \frac{dV_C}{dt} +V_C =0\]
が成り立ちます。
さきほどと同様にして、微分方程式を解いていきましょう。
\[ \frac{1}{V_C } \frac{dV_C}{dt} = – \frac{1}{RC}\]
です。両辺を\(t\)について積分すると、
\[\int _{V_C(0)}^{V_C(t)} \frac{1}{y } dy = \int_0 ^t -\frac{1}{RC} ds\]
です。したがって、
\[\log \frac{|V_C(t) |}{|V_C(0)|} = -\frac{t}{RC}\]
\[ \frac{|V_C(t) |}{|V_C(0)|}= e^{- \frac{t}{RC}}\]
です。放電を開始した時点での電圧を\(V_0 =V_C(0)\)と置くと、
\[V_C(t) = V_0 e^{- \frac{t}{RC}}\]
と電圧を求めることができました。
今回は時間経過すると、
\[\lim_{t \to \infty}V_C(t) = 0\]
と電圧が0に近づいていきます(放電が完了する)。
電流はその微分を使って求めることができます。
\[\begin{aligned} I(t) &= \frac{dQ}{dt}\\& = C \frac{dV_C}{dt} \\&=\frac{V_0}{R}e^{-\frac{t}{RC}}\end{aligned}\]
これもまた、指数関数的な減衰です。時間経過すると、
\[\lim_{t \to \infty}I(t) =0\]
となります。
以上、コンデンサーの充電・放電の時間変化について、微分方程式による説明をしてきました。
抵抗とコイルを含む回路、抵抗コイルコンデンサーの回路を流れる電流の問題についても、微分方程式の問題となります。回路における電流や電圧の時間変化は、背後に微分方程式があると知っておくと良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
数研出版 (2021-11-06T00:00:01Z)
¥867 (中古品)