どうも、木村(@kimu3_slime)です。
今回は、点電荷のガウスの法則について、導出・証明と積分形を紹介します。
点電荷のガウスの法則
電気量\(Q\)の点電荷があるとしましょう。その電場の大きさは、\(|E|= k_0 \frac{|Q|}{r^2}\)です(クーロンの法則)。
このとき、その点電荷を含む球面を考えると、そこを通る電気力線は\(N= 4\pi k_0 |Q| = \frac{|Q|}{\varepsilon_0}\)となります。
これが高校物理におけるガウスの法則です。
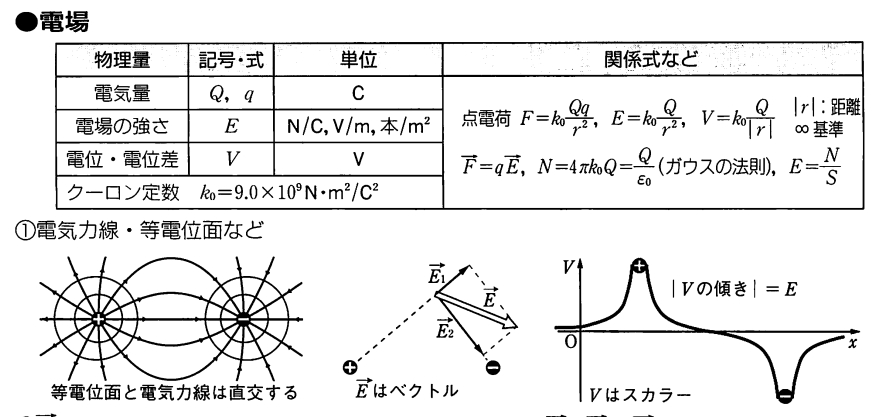
点電荷のガウスの法則を証明しましょう。
点電荷を含む半径\(r\)の球面\(S\)を考えます。電気力線の本数\(N\)とは、その定義から、単位面積当たりの本数が電場の大きさに等しいです。したがって、
\[|E| = \frac{N}{Sの表面積}\]
です。球の表面積、クーロンの法則を当てはめれば、
\[\begin{aligned} k_0\frac{|Q|}{r^2}&= \frac{N}{4\pi r^2} \end{aligned}\]
\[N = 4\pi r^2 k_0\frac{|Q|}{r^2} = 4\pi k_0 |Q|\]
とガウスの法則を導くことができました。
比例定数を\(4\pi k_0 =\frac{1}{\varepsilon_0} \)と置くことで、
\[N = \frac{|Q|}{\varepsilon_0}\]
が成り立ちます。\(\varepsilon_0\)は真空の誘電率と呼ばれるものです。
ガウスの法則の積分形
電気力線の考え方は、積分を用いて一般化することができます。
\[N = |E| \times(Sの表面積)\]
という関係があったわけですが、これを面積分
\[N = \int_S \langle E, n \rangle dS\]
に一般化するわけです。右辺の面積分を、電気力線の本数の定義としました。
\(\langle E, n \rangle\)が(微小な)面に対して垂直な(=面から出入りする)電場です。それを面\(S\)全体にわたって足し合わせる、積分したものを電気力線としたわけです。
この式から、点電荷のガウスの法則をもう一度導いてみましょう。
点電荷と球面を考えるとき、球面のどの点においても、電場は面に対して垂直です。したがって、\(\langle E, n \rangle = |E|\)です。よって、
\[\begin{aligned}N &= \int_S \langle E, n \rangle dS \\&= |E| \int_S dS\\&= 4\pi r^2 |E|\\&= 4\pi k_0 |Q|\end{aligned}\]
です。ここで面積分の定義から、\(\int_S dS\)は\(S\)曲面積となることを用いました。
電荷\(Q\)との関係式\(N = \frac{|Q|}{\varepsilon}\)を、積分を用いた電気力線の定義に当てはめると、
\[ \int_S \langle E, n \rangle dS = \frac{Q}{\varepsilon}\]
となります。これをガウスの法則の積分形と呼びます。これは電磁気学の基本法則のひとつです。
ガウスの法則が成り立つことを議論の出発点とすれば、逆にクーロンの法則を導くことができます。
点電荷においては、曲面上のどの点でも電場は面に対して垂直で、大きさが等しいです。つまり、\(\langle E, n \rangle = |E|\)です。これとガウスの法則の積分形から、
\[ |E| 4\pi r^2 = \frac{|Q|}{\varepsilon}\]
となります。\(4\pi k_0 =\frac{1}{\varepsilon_0} \)を用いて整理すれば、
\[|E| = k_0 \frac{|Q|}{r^2}\]
とクーロンの法則を導くことができました。つまり、積分形のガウスの法則は、クーロンの法則を内包する大きな原則と見ることができます。
ガウスの発散定理と呼ばれる定理を用いると、ガウスの法則は
\[ \begin{aligned}\mathrm{div}E =\frac{1}{\varepsilon_0} \rho \end{aligned} \]
が成り立つと言い換えることできます。\(\rho\)は電荷密度です。これをガウスの法則の微分形と呼びます。
電磁気学の基本的な法則は、ガウスの法則を含む4本の方程式:マクスウェル方程式としてまとめられています。これについては、大学物理、電磁気学で学ぶでしょう。
以上、点電荷のガウスの法則について、証明と積分形を紹介してきました。
比例定数の\(4\pi k_0\)は、球の表面積\(4\pi r^2\)に由来するものだったわけです。電気力線の密度、それらを足し合わせるという考えによって、面積分の考え方にもつながってくることが伝われば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
数研出版 (2021-11-06T00:00:01Z)
¥990