どうも、木村(@kimu3_slime)です。
今回は、動く(動点)とは何かについて、集合と像の考え方を紹介します。
変数が動くとは
高校の数学の問題を見ていると、変数が「動く」、動点といった用語を見かけます。これは大学数学では見かけない、独特な表現です。
1次元の例
簡単な例を通じて、その考え方を紹介しましょう。
変数\(x\)が\(1 \leq x \leq 2\)を動くとき、点\(P = (x, 2x)\)が描く軌跡を求めてみます。
関数のグラフを初めて描いたときのことを思い出しましょう。\(x\)に特定の値を当てはめて、点\(P\)を描く(プロット)していきます。
\(x= 1\)のときは、\(P=(1, 2)\)です。\(x= \frac{3}{2}\)のときは、\(P=(\frac{3}{2}, 3)\)です。\(x= 2\)のときは、\(P=(2,4)\)です。これらを平面に図示してみましょう。
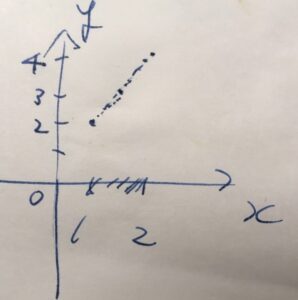
この計算では\(x= 1, \frac{3}{2}, 2\)のみしか考えていません。しかし、他の中間の細かな値についても、\( 1 \leq x \leq 2\)を満たしますね。\( 1 \leq x \leq 2\)を満たすすべての\(x\)に対して、\(P = (x, 2x)\)が動きうる範囲が軌跡です。\(x\)が時間とともに連続的に変化するようすを想像すると良いでしょう。
したがって、直線\(y=2x\)のうち、\( 1 \leq x \leq 2\)の範囲にできる線分が求める軌跡\(L\)となります。
「動く」や「軌跡」という表現を、より形式的にすると次のようになります。
変数が動く範囲は、数や点の集合として表現できます。今回は、\(I= \{x \mid 1 \leq x \leq 2\}\)です。
そして軌跡とは、関数\(f(x) = (x,2x)\)による定義域\(I\)の像(値域、取りうる値の範囲)です。
\[f(I) = \{ (x,2x) \mid x \in I\}\]
これで\(x\)が\(I\)の範囲を動くとき、\(P=(x,2x)\)が動きうる範囲を集合として表現できています。
この像をよく知られた形に変形させること、
\[\begin{aligned} f(I) &= \{ (x,2x) \mid 1 \leq x \leq 2\} \\ &= \{ (x,y) \mid 1 \leq x \leq 2 かつ y=2x\} \end{aligned}\]
が、軌跡を求める問題と言えます。
実数全体を動く例
動く範囲を変えてみましょう。
変数\(x\)が実数全体を動くとき、点\(P = (x, 2x)\)が描く軌跡はどうなるでしょうか。
実数全体を動くとは、\(x\)が実数であるならばなんでも良い、特に範囲の制限がついていないわけです。
つまり、直線\(y=2x\)が軌跡となります。
集合の言葉を使えば、定義域を実数全体\(I= \mathbb{R} \)とするとき、関数\(f(x) = (x,2x)\)による\(I\)の像は、
\[\begin{aligned} f(I) &= \{ (x,y) \mid y= 2x\} \end{aligned}\]
です。\(x,y\)は実数であるという条件は、しばしば省略されて書かれます。
平面における例
さきほどの例では、求める点\(P\)が、\(P=(x,2x)\)と動く点(変数)によって明示されていたので、簡単でした。また、動く変数\(x\)はひとつ(1次元)でした。
少し問題を難しくしてみます。点\(Q=(x,y)\)が原点から距離1を保ちながら動くとき、\(Q\)の描く軌跡を考えてみましょう。
\(x,y\)はともに実数であり、\(Q=(x,y)\)は平面上の点を表します。ただし、原点からの距離が1でなければなりません。例えば\((1,0)\)は条件を満たしますが、\((0,2)\)は条件を満たしません。
一般的に考えてみましょう。点\(Q\)と原点\(O\)の距離は、軸との間に三角形ができる斜辺の長さです。底辺が\(x\)、高さが\(y\)とすれば、三平方の定理から距離は\(x^2+y^2\)です。
したがって、距離が1となる点の軌跡は\(x^2 +y^2 =1\)です。これは円の方程式として知られています。
この問題では、\(Q\)は\((x,y)\)によって決まるものの、明確に関係式が示されていませんでした。\(Q\)は\(x^2+y^2 =1\)を満たすという関係式を導くことが、問われる問題となっています。
中点や内分する点、頂点\(Q\)の軌跡を求めよ、という問題は多いです。\(Q\)は\(x,y\)といった点の動き(変数の値)に応じて決まっているので、その関係を考察して\(x,y\)によって表せば良いでしょう。
最初は、まず実験的に条件を満たす点、満たさない点をひとつずつ試してみると良いでしょう。すると、一般的な解決法に予想がつけられます。
軌跡の問題では、「条件\(A\)を満たす点の集まりは、条件\(B\)を満たす点の集まりである」という議論をしています。議論の仕方によっては、条件\(B\)を広く取りすぎて誤った軌跡を求めてしまうので、逆の確認をしたほうが良いことがあるでしょう。
動く(動点)とは何かについて、集合と像の考え方を紹介してきました。
動点や軌跡の問題は、厳密に言えば集合や像の考え方なのですが、高校数学ではそれを伏せた問題にしています。もし「動く」という言葉の意味が気になったら、今回の話を題材に考えてみると良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
数研出版 (2019-11-01T00:00:01Z)
¥4,488 (コレクター商品)
こちらもおすすめ
ルートを含む等式の両辺を2乗するときの注意点:逆も成り立つか