どうも、木村(@kimu3_slime)です。
今回は、高校の数学で学ぶ微積分の応用として、1次反応の半減期、放射性炭素年代測定法とは何かを紹介します。
1次反応とは
五酸化二窒素\(\mathrm{N}_2 \mathrm{O}_5\)は、温めると分解して酸素を発生することが知られています。
\[2\mathrm{N}_2 \mathrm{O}_5 \to 2\mathrm{N}_2 \mathrm{O}_4 +\mathrm{O}_2\]
この分解反応の速度について考えてみましょう。実験によって、分解速度\(v\)は、物質の濃度\([\mathrm{N}_2 \mathrm{O}_5]\)に比例することが知られています。
\[v = k [\mathrm{N}_2 \mathrm{O}_5]\]
反応の速度と反応物質の濃度をの関係を表すこの式は、反応速度式と呼ばれるものです。比例定数\(k>0\)は、反応の種類や温度によって決まる定数で、反応速度定数と呼ばれています。
一般に、物質\(A\)の反応速度について、
\[v = k[A]\]
と表される反応は1次反応(first order reaction)と呼ばれます。
これに対し、\(v= k[A]^2\)となる形は2次反応と呼ばれるものです。
1次反応の例としては他に、過酸化水素水の分解、放射性元素の壊変などがあります。
1次反応の半減期
反応速度と微積分の考え方を合わせると、反応の半減期という考え方が導けます。
物質Aの濃度\([A]\)は、反応時間\(t\)に依存して変化するので、関数\([A](t)\)として見ることができます。反応速度との関係は\(v = – \frac{d[A](t)}{dt}\)です。
整理すると、関数\([A](t)\)に関する方程式
\[\frac{d[A](t)}{dt} = -k[A](t)\]
が得られます。これは一般に、微分方程式と呼ばれるものです。
特に、ニュートンの冷却法則と全く同じ形になっています。
微分方程式は、積分によって解けることが多いです。特にこの形は、変数分離ができます。
自明解\([A](t)=0\)以外の解を考えましょう。
\[ \frac{1}{[A](t)} \frac{d[A](t)}{dt} = -k\]
の両辺を積分すると、
\[ \int_{[A](0)} ^{[A](t)} \frac{1}{y} dy = \int_0 ^t -k ds\]
となります。
左辺は対数関数です。
\[\begin{aligned} \int_{[A](0)} ^{[A](t)} \frac{1}{y} dy&=[\log y]_{[A](0)} ^{[A](t)} \\&= \log [A](t) – \log [A](0) \\&= \log \frac{[A](t)}{[A](0)}\end{aligned}\]
したがって、
\[\log \frac{[A](t)}{[A](0)} = -kt\]
となりますが、ここで両辺の指数関数を取ると、対数関数は指数関数の逆関数なので外れて、
\[[A](t) =[A](0) e^{-kt}\]
と求めることができました。これは指数関数的な減衰ですね。
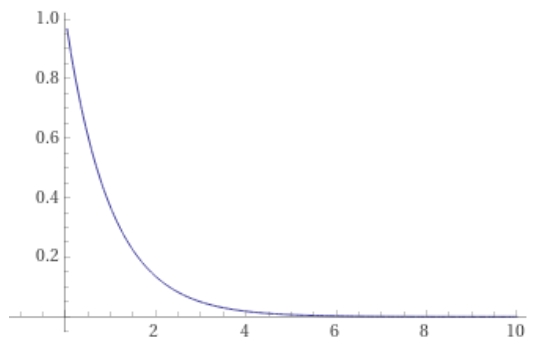
物質の濃度が初期濃度の半分となる時間\(T\)を、半減期と呼びます。
1次反応の半減期を求めてみましょう。
\[[A](0) e^{-kT} = \frac{1}{2}[A](0)\]
を満たすので、両辺の対数を取れば、
\[-kT = \log \frac{1}{2}\]
\[T = \frac{\log_{e} 2}{k}\]
となりました。これは最初の濃度\([A](0)\)によらず、反応定数\(k\)のみによって決まっていますね。
放射性炭素年代測定法
半減期の考え方は、過去の動物や植物の化石や遺骸から、それら生きていた時期を推定する、年代測定法に応用されます。
生きている動植物では、炭素の同位体、炭素14\({}^{14}\mathrm{C}\)の比率が一定であることが知られています。亡くなるとその比率は一定でなくなり、窒素14\({}^{14}\mathrm{N}\)へとβ線を出しながら崩壊します。
\[{}^{14}\mathrm{C} \to {}^{14}\mathrm{N} +\beta\]
炭素14の半減期は、約5730年です。
遺骸の炭素14の割合と半減期を利用することで、動植物が生きていた時期を推測する方法は、放射性炭素年代測定法と呼ばれています。
これは実際に利用されている方法です。
参考:2.海の年代を示す放射性炭素 – 六甲の森と大阪湾の誕生

ある貝の化石における炭素14の濃度が、\(\frac{2}{3}\)になっていたとしましょう。この貝は何年前まで生きていたと推測できるでしょうか。生きていた時刻を\(0\)、現在を\(t\)とします。
濃度が初期濃度の\(\frac{2}{3}\)となっていたことから、
\[[{}^{14}\mathrm{C}](0) e^{-kt} = \frac{2}{3}[{}^{14}\mathrm{C}](0)\]
なので、対数を取れば
\[-kt = \log \frac{1}{4}\]
\[t = \frac{\log_{e} \frac{3}{2}}{k}\]
です。反応速度定数は、半減期の関係から
\[k= \frac{\log_{e} 2}{5730}\]
と求められます。よって、
\[\begin{aligned} t &= 5730\times \frac{\log_{e} \frac{3}{2}}{\log_e 2}\\&\approx 3352 \end{aligned}\]
となりました。約3000年前のものであることがわかりますね。
以上、高校の数学で学ぶ微積分の応用として、1次反応の半減期、放射性炭素年代測定法とは何かを紹介してきました。
化学物質の分解のスピードについて考えるのに微積分が役立つこと、その応用として過去の動植物が生きていた時期を推定できることが伝われば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
数研出版 (2021-11-06T00:00:01Z)
¥933 (中古品)
三省堂 (2018-12-26T00:00:01Z)
¥1,566 (中古品)