符号検定、ノンパラメトリック検定とは：Juliaによる実践例

どうも、木村（@kimu3_slime）です。

今回は、符号検定とは何か、Juliaによる実践例を交えて紹介します。

符号検定とは
Juliaによる実践例
こちらもおすすめ

符号検定とは

2つの映画を30人に5段階評価してもらったところ、次のようなデータが得られたとしましょう。

このとき、2つの評価に違いがあると言えるでしょうか？　特に、中央値に違いがあると言えるでしょうか。それを調べる仮説検定が、符号検定です。

2つのサンプル\(x,y\)は、連続確率変数\(X,Y\)によって独立に生み出されると考えましょう。サンプルサイズをともに\(n\)とします。

このとき、\(p = P(X\geq Y)\)として、帰無仮説を

\[H_0 : p= \frac{1}{2}\]

としましょう。これは差\(X-Y\)の中央値が0であるという仮説です。累積した確率がちょうど\(1/2\)となるのが、中央値の定義なので。対立仮説は、\(H_1 : p \neq \frac{1}{2}\)とします。

この仮説を調べるため、サンプルの差の符号を調べる確率変数

\[Z_i= \begin{cases}1 & (X_i-Y_i \geq 0 )\\0 & (X_i-Y_i < 0)\end{cases}\]

を用意しましょう。そして、

\[\begin{aligned} U = \sum_{i=1}^n Z_i \end{aligned}\]

という確率変数を考えます。差を取ったときに、プラスになる組の個数です。

もし帰無仮説が正しいならば、\(Z_i\)はベルヌーイ分布で、\(U\)はその和なので、二項分布\(\mathrm{Binomial}(n,\frac{1}{2})\)に従います。

したがって、差の符号の個数合計\(U\)によって中央値が0であるという仮説が調べられます。これは中央値の符号検定（sign test）と呼ばれるものです。

この方法では、サンプルの母集団分布\(X,Y\)に特定の分布、例えば正規分布であることを仮定しませんでした。したがって、特定の母集団分布に関するパラメータの推定でもありません。このような検定は、一般にノンパラメトリック検定（nonparametric test）と呼ばれています。分布によらない検定（distribution-free test）とも。

Juliaによる実践例

コンピュータ、Juliaによって符号検定を行ってみましょう。

まず、比較したい2つのサンプル、30人による2つの映画の5段階評価を、乱数によって用意します。

using Distributions, HypothesisTests, Random, Plots

Random.seed!(2022)
x = rand(DiscreteUniform(1,5),30)

using Distributions, HypothesisTests, Random, Plots

Random.seed!(2022)

x = rand(DiscreteUniform(1,5),30)

30-element Vector{Int64}:
 1
 5
 3
 4
 3
 4
 3
 5
 1
 1
 4
 3
 5
 ⋮
 3
 5
 2
 5
 2
 4
 4
 3
 4
 4
 2
 4

30-element Vector{Int64}:

⋮

Random.seed!(2022)
y = rand(Binomial(5,1/3)+1,30)

1 2	Random.seed!(2022) y = rand(Binomial(5,1/3)+1,30)

30-element Vector{Int64}:
 2
 2
 2
 3
 3
 2
 3
 2
 1
 2
 3
 2
 1
 ⋮
 3
 2
 1
 2
 3
 2
 3
 4
 1
 4
 4
 4

30-element Vector{Int64}:

⋮

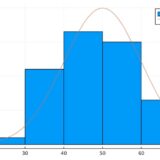
冒頭で示したヒストグラムは、このサンプルによるものです。

histogram(x, alpha=0.5)
histogram!(y, alpha=0.5)

1 2	histogram(x, alpha=0.5) histogram!(y, alpha=0.5)

「SignTest(x,y)」によって、差の中央値が0であるという帰無仮説に関する符号検定ができます。

SignTest(x,y)

1	SignTest(x,y)

Sign Test
---------
Population details:
    parameter of interest:   Median
    value under h_0:         0.0
    point estimate:          1.0
    95% confidence interval: (0.0, 2.0)

Test summary:
    outcome with 95% confidence: reject h_0
    two-sided p-value:           0.0347

Details:
    number of observations:       23
    observations larger than 0.0: 17