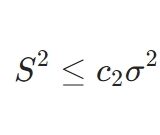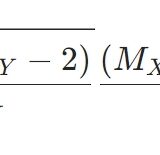どうも、木村(@kimu3_slime)です。
今回は、2サンプルの平均の差の検定について、等サイズ等分散のケースを、Juliaを使って紹介します。
2サンプルの平均の差の検定
検定の原理と手順
10人の人にあるテストを受けてもらい、1ヶ月後再び同じテストを受けてもらい、点数が次のようになったとしましょう。
1 2 3 4 | using HypothesisTests, Distributions, Random Random.seed!(2022) x = rand(Normal(50,10),10) |
1 2 3 4 5 6 7 8 9 10 11 | 10-element Vector{Float64}: 50.6912301164913 38.84399961848597 42.84480604223728 60.9769650429804 54.978651946367876 33.951339022096505 40.96806064167559 32.42960541746047 49.11909337153176 48.368593011534614 |
1 2 | Random.seed!(2023) y = rand(Normal(60,10),10) |
1 2 3 4 5 6 7 8 9 10 11 | 10-element Vector{Float64}: 57.23376737326983 53.31042496456294 33.575638089991145 69.02873395966154 49.88661922990406 77.13082098104172 73.73711455313895 52.50792918471635 60.55878925411058 55.519917656199226 |
それぞれの平均を計算してみると、
1 | mean(x),mean(y) |
1 | (45.31723442308618, 58.248975524659635) |
差には違いがある、2回目の方が大きいように見えます。ただし、この数字を比較するだけでは、たまたま偶然によるブレがあったと言えるかもしれません。
そこで、2つのサンプルの差について、検定を行いましょう。
今回は、
- 2つのサンプルは正規分布に従っていて、分散が等しい
- 2つのサンプルのサイズが等しい
という仮定を置きます。これはペアのt検定(paired t test)、対応のある2つのグループの平均値の差の検定と呼ばれるものです。
2つのサンプルの母集団の平均を\(\mu_X ,\mu _Y\)とし、分散が等しく、サンプルサイズを\(n\)としましょう。そしてサンプルの差の平均を\(M_D\)、サンプルの差の不偏分散を\(S_D^2\)とします。このとき、
\[T= \frac{M_D-(\mu_X -\mu_Y)}{\frac{S_D}{\sqrt{n}}}\]
は自由度\(n-1\)のt分布に従うことが知られています。
帰無仮説として
\[H_0: \mu_X = \mu _Y\]
対立仮説として
\[H_1: \mu_X \neq \mu _Y\]
を設定しましょう。一方は平均の差が0、もう一方は平均の差が0でない、という仮説です。
有意水準を\(\alpha\)として決めたとき、帰無仮説が正しい仮定のもとで、
\[P(c_1 \leq T \leq c_2) = 1-\alpha\]
となる区間を求めることができます。
- サンプルの差がこの区間に入るならば、帰無仮説は棄却されない
- サンプルの差がこの区間に入らないならば、帰無仮説は棄却される
という考え方で、検定を行えます。
検定のやり方
以上が平均の差の検定の原理です。ここからは、実際に検定を行ってみましょう。
JuliaのパッケージHypothesisTestsでは、「OneSampleTTest(x,y)」で平均の差が0であるという仮説を検定できます。
1 | OneSampleTTest(x,y) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | One sample t-test ----------------- Population details: parameter of interest: Mean value under h_0: 0 point estimate: -12.9317 95% confidence interval: (-24.32, -1.546) Test summary: outcome with 95% confidence: reject h_0 two-sided p-value: 0.0302 Details: number of observations: 10 t-statistic: -2.5693406856844194 degrees of freedom: 9 empirical standard error: 5.033097079583555 |
最初に示したサンプルを検定すると、有意水準が\(\alpha =0.05\)のときは、仮説が棄却されることがわかりました。平均に差があるという仮説が支持されたわけです。
一方で、帰無仮説が棄却される最小の有意水準の値=p値は0.03です。\(\alpha=0.01\)と設定していたときは、帰無仮説は棄却されない、平均に差がない可能性が否定されません。
差の検定においては、帰無仮説が棄却されることを有意差(significant difference)がある、棄却されないことを有意差があるとは言えない、という言葉遣いがされることがあります。この「有意」という用語は、確率統計的に違いがある可能性が高いということであり、「差の結果に科学的な意義がある」ことを意味しないことに注意しましょう。
母集団の平均が近いサンプルを用意すると、平均に差があるという仮説は棄却されなくなります。
1 2 3 4 5 | Random.seed!(2022) x = rand(Normal(50,10),10) Random.seed!(2023) y = rand(Normal(55,10),10) OneSampleTTest(x,y) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | One sample t-test ----------------- Population details: parameter of interest: Mean value under h_0: 0 point estimate: -7.93174 95% confidence interval: (-19.32, 3.454) Test summary: outcome with 95% confidence: fail to reject h_0 two-sided p-value: 0.1495 Details: number of observations: 10 t-statistic: -1.57591657306752 degrees of freedom: 9 empirical standard error: 5.033097079583555 |
同じ平均の設定のもとで、サンプルサイズを大きくすると、平均の違いが検知されるようになります。
1 2 3 4 5 | Random.seed!(2022) x = rand(Normal(50,10),100) Random.seed!(2023) y = rand(Normal(55,10),100) OneSampleTTest(x,y) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | One sample t-test ----------------- Population details: parameter of interest: Mean value under h_0: 0 point estimate: -7.40142 95% confidence interval: (-10.31, -4.492) Test summary: outcome with 95% confidence: reject h_0 two-sided p-value: <1e-05 Details: number of observations: 100 t-statistic: -5.047542753105441 degrees of freedom: 99 empirical standard error: 1.4663412197116885 |
サンプルサイズが小さいと、仮に平均に差があったとしても、検定で見抜けない可能性があるわけです。
逆に気をつけたいのが、どんなに小さな平均の差であったとしても、サンプルサイズを増やして検定をすれば、平均に差があるという仮説が棄却されなくなります。「差の有無」は、「差の大小」を必ずしも意味しないことに注意しましょう。
最後に、有意水準に関する検証をしましょう。
何度も検定を繰り返したとき、帰無仮説が正しいにもかかわらずそれを棄却する割合が有意水準\(\alpha\)です。
母集団分布の平均に差がないデータを与えて、棄却される割合を計算してみましょう。「pvalue(検定)」で、検定のp値を求められます。
1 2 3 4 5 6 7 8 9 10 11 12 | k = 10^3 α = 0.05 rej = 0 for i in 1:k x = rand(Normal(50,10),10) y = rand(Normal(50,10),10) if pvalue(OneSampleTTest(x,y)) < α rej += 1 else end end rej/k |
1 | 0.05 |
1000回サンプルを取って検定を繰り返した結果、約5%が棄却されました。これが有意水準\(\alpha =0.05\)の意味ですね。
以上、2サンプルの平均の差の検定について、等サイズ等分散のケースを、Juliaを使って紹介してきました。
今回はサンプルサイズが同じ場合を扱いましたが、サイズが異なる場合でも似た方法が使えます。それについては別記事で紹介予定です。
木村すらいむ(@kimu3_slime)でした。ではでは。
Probability and Statistics: Pearson New International Edition
Pearson Education Limited (2013-07-30T00:00:01Z)
¥10,792 (中古品)
培風館 (1978-01-01T00:00:01Z)
¥5,280
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥5,862 (中古品)
こちらもおすすめ
統計的仮説検定とは:平均の検定、t検定を例に、Juliaを使って