どうも、木村(@kimu3_slime)です。
今回は、ポアソン分布の歪度・尖度の求め方について、モーメント・キュムラント生成関数を使った方法を紹介します。
ポアソン分布のモーメント生成関数
まず、\(X\)を単位時間あたりの発生頻度\(\lambda\)のポアソン分布\(\mathrm{Poisson}(\lambda)\)として、そのモーメント生成関数を求めましょう。
ポアソン分布の確率質量関数は
\[f(k)= e^{-\lambda }\frac{\lambda^k}{k!}\]
\(k=0,1,2,\dots\)なので、モーメント生成関数は
\[\begin{aligned} M_X(t) &= E(e^{tX})\\&=\sum _{k=0}^\infty e^{tk} e^{-\lambda }\frac{\lambda^k}{k!}\\&=e^{-\lambda} \sum _{k=0}^\infty \frac{(\lambda e^{t})^k}{k!} \\&=e^{-\lambda}\exp(\lambda e^{t}) \\&= \exp(\lambda e^{t} -\lambda)\end{aligned}\]
となります。\(\exp\)は指数関数であり、そのテイラー展開
\[\exp(x) =\sum_{k=0}^\infty \frac{x^k}{k!}\]
を用いました。
ポアソン分布の歪度・尖度
したがって、ポアソン分布のキュムラント生成関数は
\[\begin{aligned} K_X(t)&=\log (M_X(t)) \\&= \lambda e^{t} -\lambda \end{aligned} \]
となるので、その微分は
\[\frac{d^n}{dt^n}K_X(t) =\lambda e^{ t}\]
であり、キュムラントは
\[\kappa_n = \frac{d^n}{dt^n}K_X(0)=\lambda\]
\(n=1,2,\dots\)となります。
よって、歪度・尖度とキュムラントの関係式から、
\[V(X) = \kappa_2 =\lambda\]
\[\begin{aligned} \frac{E((X-E(X))^3)}{(\mathrm{Std}(X))^3} &= \frac{\kappa_3}{(\mathrm{Std}(X))^3} \\&= \frac{\lambda}{\lambda^{\frac{3}{2}}} \\&= \frac{1}{\sqrt{\lambda}}\end{aligned}\]
\[\begin{aligned} \frac{E((X-E(X))^4)}{(\mathrm{Std}(X))^4}-3 &= \frac{\kappa_4}{(\mathrm{Std}(X))^4} \\&= \frac{\lambda}{ \lambda ^2}\\&= \frac{1}{\lambda}\end{aligned}\]
と求めることができました。
いくつかのパラメータについて、ポアソン分布の確率質量関数を描いてみます。
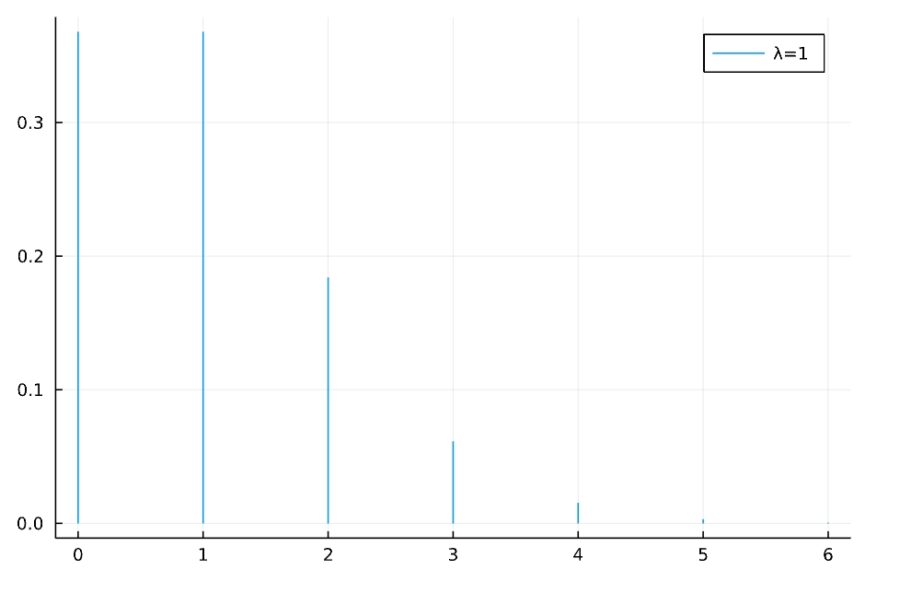
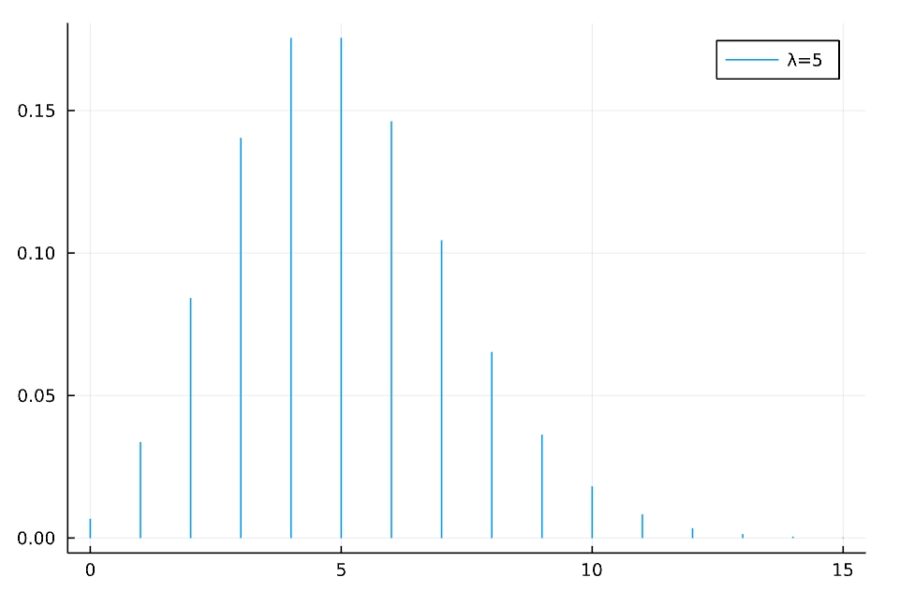
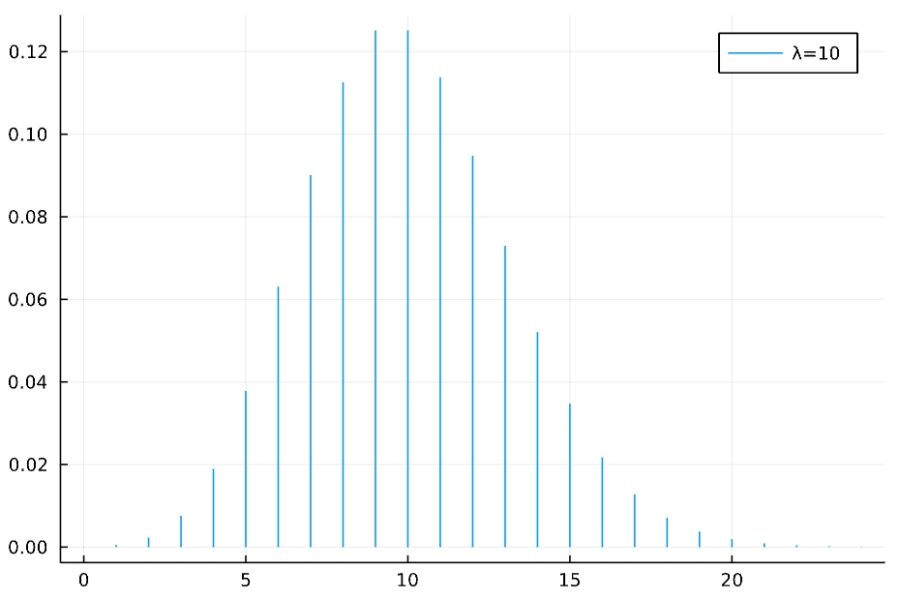
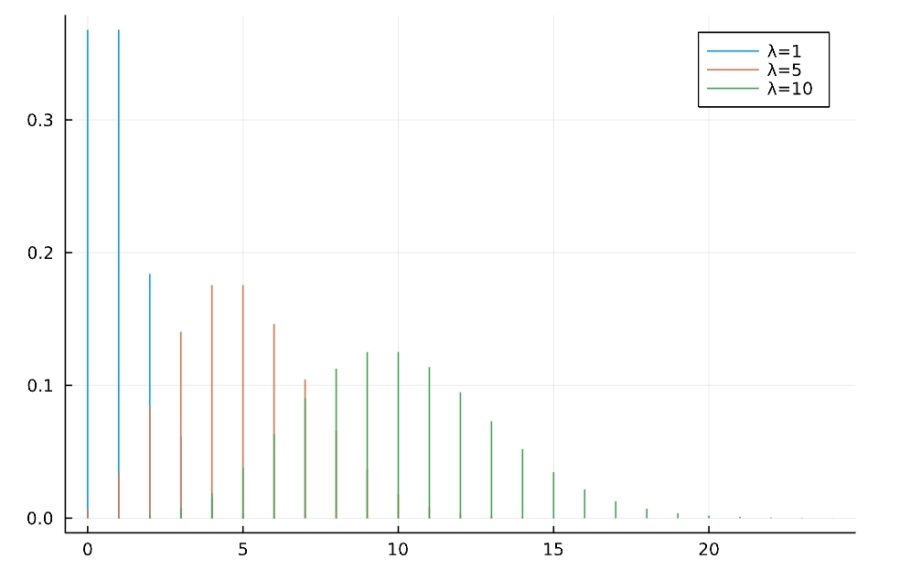
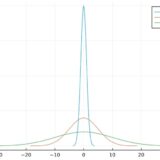
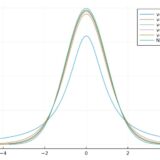
歪度は\(\frac{1}{\sqrt{\lambda}}\)なので、\(\lambda\)が大きくなるほど0に近づいていきます。実際、\(\lambda=1\)では左側への偏りが大きく、\(\lambda=10\)では左右対称に近づいています。
尖度は\(\frac{1}{\lambda}\)であり、同じく\(\lambda\)が大きくなるほど0に近づいていきます。\(\lambda=1\)では平均値付近の比重が大きく尖っていますが、\(\lambda=10\)では裾の比重がより大きくなっています。
\(\lambda\)を大きくするとポアソン分布の歪度・尖度は、正規分布の歪度・尖度(ともに0)に近づいています。これはポアソン分布の\(\lambda \to \infty\)での極限が正規分布である、という結果に対応するものです。
以上、ポアソン分布の歪度・尖度の求め方について、モーメント・キュムラント生成関数を使った方法を紹介してきました。
歪度・尖度の考え方は、正規分布と比較してみるとわかりやすいですが、その例としてポアソン分布は計算しやすくて良いですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Probability and Statistics: Pearson New International Edition
Pearson Education Limited (2013-07-30T00:00:01Z)
¥10,792 (中古品)
培風館 (1978-01-01T00:00:01Z)
¥5,280
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥5,862 (中古品)
こちらもおすすめ
離散確率分布とは:一様分布、ベルヌーイ分布、二項分布、ポアソン分布を例に