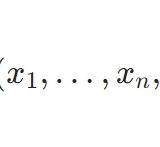どうも、木村(@kimu3_slime)です。
今回は、点推定、不偏推定量とは何か、平均と分散を例に紹介します。
点推定
点推定(point estimate)とは、統計モデルにおけるパラメータを、サンプルから特定の数値=実数上の点として推測することです。
点推定という用語は、実数上のある区間内にパラメータがあると推測する区間推定と対になっています。
最も簡単な点推定は、次の統計量を用いた平均と分散の推定です。\(X_1,\cdots,X_n\)をランダムサンプリングに対応する確率変数(独立同分布)とするとき、
\[\hat{\mu} = \frac{1}{n}\sum_{k=1}^n X_k\]
\[\hat{\sigma}^2 = \frac{1}{n-1}\sum_{k=1}^n (X_k- \hat{\mu})^2\]
によって推測します。ハット\(\hat{}\)は推定量であることを表す記号で、それぞれ母集団分布\(X\)の平均\(\mu\)、分散\(\sigma^2\)の推定量を表しています。
分散の推定値の分母が\(n-1\)になっていることに注意しましょう。これは不偏分散(unbiased variance)と呼ばれるものです。
母集団分布の平均と分散が未知であったとして(実際にはこちらは答えを知っていますが)、コンピュータ上で乱数によって得られたデータから推測してみましょう。Juliaを使っています。
1 2 3 4 5 6 7 8 | using StatsPlots, Random, Distributions d1 = Normal(50,20) Random.seed!(2022) x = rand(d1,30) mean(x) var(x) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | 30-element Vector{Float64}: 51.382460232982595 27.68799923697193 35.68961208447456 71.9539300859608 59.95730389273575 17.902678044193003 31.93612128335118 14.859210834920944 48.23818674306352 46.73718602306923 40.260926885377465 82.06269505812217 88.57815487400246 ⋮ 37.19042229709257 0.22819171326523247 62.113209956248376 73.15193525902828 38.437951112682555 65.84039250831833 72.144844132213 27.944528938385087 73.43477100834359 70.79726268099043 57.01415666515274 66.5381054157689 |
1 2 | 48.662682436632274 495.36697545737127 |
30個のサンプルから推定したとき、\(\hat{\mu}\sim 48.7\)、\(\hat{\sigma}^2 \sim 495 \)となりました。元の分布では\(\mu =50\)、\(\sigma^2 =400\)なので、悪くはありません。
サンプルを1000個に増やすと、\(\hat{\mu} \sim 49.5\)、\(\hat{\sigma}^2 \sim 427\)となり、かなり近づいています。
不偏推定量
パラメータを点推定するときに、推定に使う統計量(=推定量)に求める性質のひとつが、何回も推定をすればその平均が母集団のパラメータに近づいていく性質です。
\(g(X_1,\dots,X_n)\)を統計量とし、\(\theta\)を母集団分布のパラメータとしましょう。\(g(X_1,\dots,X_n)\)が不偏推定量(unbiased estimator)であるとは、すべての\(\theta \)について\(E(g(X_1,\dots,X_n))= \theta\)が成り立つことです。
\(g(X_1,\dots,X_n)\)はサンプルを使って計算される量ですが、その平均(期待値)がパラメータに一致しているということは、何回も推定をすればその量の平均(期待値)はパラメータに近づくということです(大数の法則)。
平均の推定量
\[\hat{\mu} = \frac{1}{n}\sum_{k=1}^n X_k\]
が不偏推定量であることを確かめてみましょう。
\[\begin{aligned} E(\hat{\mu}) &= \frac{1}{n} \sum_{k=1}^n E(X_k) \\&= \frac{1}{n} n \mu \\&= \mu \end{aligned}\]
が成り立ちます。\(X_1,\dots, X_k\)は同じ分布\(X\)に従っているので、期待値\(\mu =E(X)=E(X_k)\)は一致しています。
分散の推定量(不偏分散)
\[\hat{\sigma}^2 = \frac{1}{n-1}\sum_{k=1}^n (X_k- \hat{\mu})^2\]
が不偏推定量であることを確かめてみましょう。計算によって、
\[\begin{aligned} &E(\hat{\sigma}^2) \\&= \frac{1}{n-1}E(\sum_{k=1}^n (X_k -\hat{\mu})^2)\\&= \frac{1}{n-1}E(\sum_{k=1}^n ((X_k – \mu) + (\mu -\hat{\mu}))^2) \\&= \frac{1}{n-1}E(\sum_{k=1}^n( (X_k – \mu)^2 +2(X_k-\mu) (\mu -\hat{\mu})+(\mu-\hat{\mu})^2 )) \\&= \frac{1}{n-1}\sum_{k=1}^n E((X_k-\mu)^2) \\ &\quad +\frac{2}{n-1}E((\mu-\hat{\mu})\sum_{k=1}^n (X_k-\mu)) \\ &\quad +\frac{n}{n-1}E((\mu-\hat{\mu})^2 ) )\\&= \frac{n}{n-1}\sigma^2 \\ &\quad -\frac{2n}{n-1}E((\mu-\hat{\mu})^2 ) )\\ &\quad+\frac{n}{n-1}E((\mu-\hat{\mu})^2 ) ) \\&= \frac{n}{n-1}\sigma^2 -\frac{n}{n-1} E((\mu-\hat{\mu})^2)\\&=\frac{n}{n-1}\sigma^2-\frac{n}{n-1}V(\hat{\mu})\\&= \frac{n}{n-1}\sigma^2 – \frac{n}{n-1}\frac{1}{n^2}\sum_{k=1}^n V(X_k)\\&= \frac{n}{n-1}\sigma^2 – \frac{n}{n-1}\frac{n}{n^2}\sigma^2 \\&=\sigma ^2\end{aligned}\]
となることがわかります。
途中の積の計算で、
\[\begin{aligned} \mu -\hat{\mu} &= \frac{1}{n}\sum_{k=1}^n \mu -\frac{1}{n}\sum{k=1}^n X_k \\&= \frac{1}{n}\sum_{k=1}^n(\mu-X_k) \end{aligned}\]
という変形を利用しました。
\(E((X_k-\mu)^2) = E((X-E(X))^2)=\sigma^2\)は、分散の定義と、同じ分布に従っていることによります。
\(V(\hat{\mu})\)の計算では、分散の定数倍(外に出すと2乗になる)、和の性質を利用しました。和の性質を使うために、確率変数の独立性という仮定が効いていることに注意しましょう。
分母を\(n\)とするサンプル分散(補正のない分散)の期待値は、
\[E(\frac{1}{n} \sum_{k=1}^n(X_k -\mu)^2) =(1-\frac{1}{n}) \sigma ^2\]
となり、常に\(\sigma ^2\)より小さくなってしまいます。そこで不偏推定量である
\[\hat{\sigma}^2 = \frac{1}{n-1}\sum_{k=1}^n (X_k- \hat{\mu})^2\]
を用いることが多いわけですね。これが分母に\(n-1\)をつけて分散を計算する理由です。\(n\)が大きいときには差がありませんが、小さい時には影響が大きくなります。
Juliaでは、varが不偏分散、オプションで「corrected = false」を指定すると補正のない分散が計算できます。
1 2 3 4 5 6 7 8 9 10 11 12 13 | k = 100 unbiased = zeros(k) uncorrected = zeros(k) for i in 1:k x = rand(d1,20) unbiased[i] = var(x) uncorrected[i] = var(x,corrected=false) if i == k println(mean(unbiased)) println(mean(uncorrected)) else end end |
1 2 | 401.6192946253757 381.53832989410677 |
「20個のサンプルから不偏分散、補正のない分散を求める」ことを100回繰り返した結果、不偏分散の平均が約402、補正なし分散の平均が約382となりました。前者はかなりよく推定ができています。
サンプル数が少ないので、個別には取ってきたサンプル(乱数)によるブレがあります。補正のない分散のほうが、結果的に母集団の分散に近いこともありえます。
しかし長期的には、補正された不偏分散の方が母集団の分散をよく推定しているわけですね。
以上、点推定、不偏推定量とは何か、平均と分散を例に紹介してきました。
推定の手順自体はかなり簡単なので、その意味や仕組みを合わせて知ってもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Probability and Statistics: Pearson New International Edition
Pearson Education Limited (2013-07-30T00:00:01Z)
¥10,792 (中古品)
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥5,862 (中古品)
こちらもおすすめ
Juliaで確率分布に従う乱数、確率関数、累積分布関数を描く方法