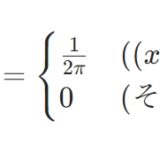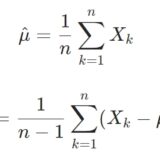統計モデル、統計的推測、パラメータ、統計量とは

どうも、木村（@kimu3_slime）です。

今回は、統計モデル、統計的推論、パラメータ、統計量とは何かについて紹介します。

記述統計と推測統計
統計モデル、統計的推測、パラメータ、統計量
こちらもおすすめ

記述統計と推測統計

初等的な統計学の教科書は、主に2つの分野を扱っています。それが記述統計学（descriptive statistics）と推測統計学（inferential statistics）です。

前者は与えられたデータをわかりやすく要約することについてです。ヒストグラムを作ったり、データの平均や分散の計算をします。

後者は与えられたデータをもとに、それを生み出している確率的なモデル、統計モデルに関する推測を扱います。これについてもっと詳しく述べていきましょう。

統計モデル、統計的推測、パラメータ、統計量

例えば、ある「コイン」を1000回投げて、うち約800回が表、200回が裏というデータが得られたとします。

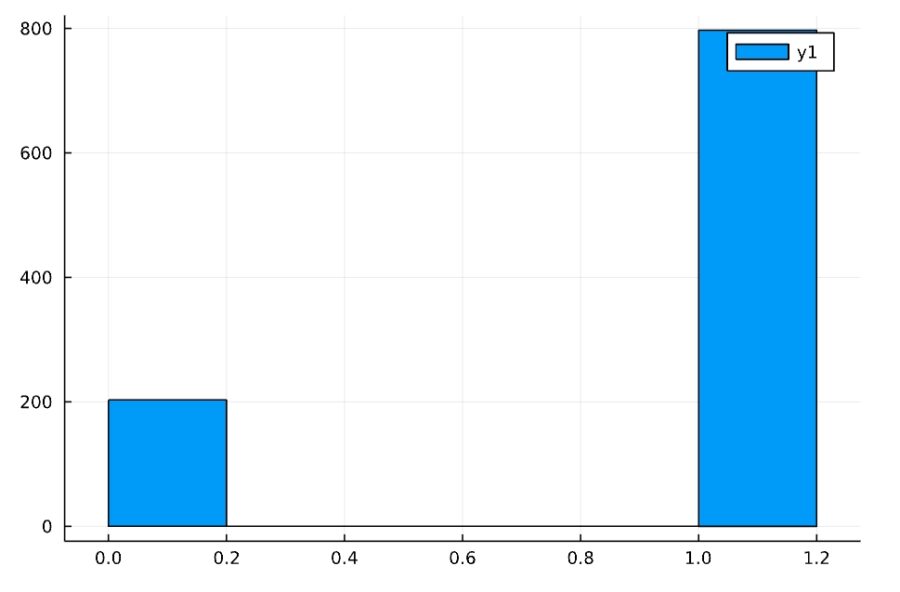
このコインは公平でしょうか？　表と裏が出る確率が同じと推測するのは、流石に妥当ではなさそうです。

確率と統計の用語を知っていると、この状況は次のように定式化できるでしょう。このコインの表と裏のでやすさは、試行によって変わらないと仮定する。取りうる値は2種類なので、ベルヌーイ分布\(d= \mathrm{Bernoulli}(p)\)に従う確率変数\(X\)を考えることになります。

1000個のデータ\(x_1,x_2,\dots,x_{1000}\)は、\(X\)からランダムに取り出されたサンプルです。つまり同じ分布\(X\)に従う確率変数族\(X_1,X_2,\dots,X_{1000}\)があり、それらは独立であると仮定しています。目の前のデータを、ある確率分布に従って実現された値と捉えているわけですね。

ベルヌーイ分布にはパラメータ、表の出やすさ\(p\)があります。ここでは、表と裏の全体での比率、つまり平均\(\frac{800}{1000}=0.8\)をその推測に使えそうです。こうして、「このコインは確率\(0.8\)で表が出るコインだろう」と、データを使って統計的に推測することができました。（この推測が正しいかどうかは保留します）

この流れをまとめましょう。

統計モデル（statistical model）は、調べたい現象の確率変数\(X_1,X_2,\dots\)や確率分布\(d\)を特定したり、その分布が持つパラメータ\(\theta\)は何か、パラメータの値を観測データから推測したりすることです。モデルとは、現象（データ）を近似・説明するために使う理論的な概念のことです。

そして、統計的推測（statistical inference）とは、統計モデルについて確率論の考え方を使った主張をすることです。

例えば、コイン投げ1000回については、ベルヌーイ分布やそれに従う確率変数、パラメータ\(p\)を想定しましたが、それらが考えている統計モデルです。「\(p=0.8\)である」という主張が、統計的推測ですね。

統計モデルにおける確率変数の値\(X_i(\omega)=x_i\)を、観測値、実現値（observable）、観測可能変数と呼ぶことがあります。

僕たちが得られる観測値は有限個ですが、コインの例が示すように、パラメータの値そのものは厳密には無限の観測が必要です。したがって、つまり大量に測定して近づいていく値を使って推測することになります。このパラメータを例とする確率変数を、仮説的な観測値（hypothetically observable）と呼びます。

パラメータ（parameter）とは、確率変数\(X_1,\dots,X_n\)の同時分布を特徴づける数、または数の集まりのことです。媒介変数、母数とも。

例えばポアソン分布ならば単位時間あたりの発生頻度\(\lambda\)、正規分布ならば平均\(\mu\)、分散\(\sigma ^2\)がパラメータです。

平均や分散といったデータ・確率変数を使って計算される量は、まとめて統計量と呼ばれます。

例えば、

\[M_n = \frac{1}{n}\sum_{k=1}^n X_k\]

という確率変数は、サンプル平均です。

一般に、複数の確率変数\(X_1,\dots,X_n\)と多変数の実数値（可測）関数\(g\)を組み合わせてできる確率変数\(Y=g(X_1,X_2,\dots,X_n)\)を、統計量（statistic）と呼びます。

サンプル平均ならば、\(g(x_1,\dots,x_n)= \frac{1}{n}\sum_{k=1}^n x_k\)という多変数関数を考えているわけです。中央値、最小値、最大値、尖度や歪度は統計量の例ですね。

以上、統計モデル、統計的推論、パラメータ、統計量とは何かについて紹介してきました。

統計的推論の具体的な問題には、推定、仮説検定、相関・回帰分析などがあります。これらについては別記事で紹介します。

木村すらいむ（@kimu3_slime）でした。ではでは。