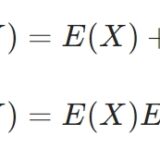どうも、木村(@kimu3_slime)です。
今回は、確率変数の独立性とは何か、具体例と性質を紹介します。
確率変数の独立性
結果全体の集合:サンプル空間を\(\Omega\)、そこにおける確率(測度)を\(P\)としましょう。
事象\(A, B \subset \Omega\)が独立であるとは、\(P(A\cap B)=P(A)P(B)\)(積の法則)が成り立つことでした。
同時に起こる確率が、個別の確率の積として計算できることが、独立に起こるということの意味です。
この考え方の一般化として、2つの確率変数の独立性が考えられます。
\(X : \Omega_1 \to \mathbb{R}\)、\(Y : \Omega_2 \to \mathbb{R}\)を離散または連続確率変数としましょう。
\(X,Y\)が互いに独立である(independent)とは、すべての部分集合\(A_1 , A_2 \subset \mathbb{R}\)に対し、\(P(X \in A_1 , Y \in A_2)= P(X \in A_1) P(Y \in A_2)\)が成り立つことです。
\(X \in A_1 , Y \in A_2\)のコンマ\(,\)は「かつ」の意味であることに注意しましょう。
確率変数の独立性の考え方は、事象の独立性の一般化になっています。
事象\(A,B \subset \Omega\)が与えられた時、特殊なケースとして、
\[X(\omega)= \begin{cases}1 & (\omega \in A )\\0 & (それ以外)\end{cases}\]
\[Y(\omega)= \begin{cases}1 & (\omega \in B )\\0 & (それ以外)\end{cases}\]
と対応する確率変数(指示関数)を考えると、\(X,Y\)が独立であるならば、\(A,B\)が独立になります。(長くなるので省略しますが、逆も成り立ちます。)
なぜか。まず\(X,Y\)が独立であるとすると、\(A_1 =A_2=\{1\}\)とすることで、\(P(X=1,Y=1)=P(X=1)P(Y=1)\)が成り立ちます。\(X,Y\)の定義から、\((X=1)= \{\omega \in \Omega \mid X(\omega )=1\} =A\)、\((Y=1)=B\)なので、\(P(A\cap B)=P(A)P(B)\)となることがわかりました。
確率変数が独立であることの定義は、意味はわかりやすいですが、すべての事象\(A_1,A_2\)について考えるため、判定しにくいです。そこで、複数の同値な条件が知られています。
\(X,Y\)の確率(質量・密度)関数を\(f_X, f_Y\)、同時確率(質量・密度)関数を\(f_{X,Y}\)、累積分布関数をそれぞれ\(F_X,F_Y,F_{X,Y}\)とする。
このとき、次の条件は同値である。
- \(X,Y\)が独立である
- すべての\(x,y \in \mathbb{R}\)に対し、\(f_{X,Y}(x,y)=f_X(x)f_Y(y)\)
- すべての\(x,y \in \mathbb{R}\)に対し、\(F_{X,Y}(x,y)=F_X(x)F_Y(y)\)
つまり、確率関数か累積分布関数が積の形に分離されることによって、独立性が判定できます。
これを使って、どのような確率変数が独立なのか、調べてみましょう。
具体例
離散確率変数
公平なサイコロ投げについて考えるとして、\(\Omega =\{1,\dots,6\}\)、\(P\)として離散一様分布を考えましょう。
2回サイコロを投げ、\(X,Y\)をそれぞれの出た目とします。\(X(\omega)=Y(\omega)=\omega\)とするわけです。
このとき、\(X,Y\)は独立です。
\(X,Y\)が一様分布に従っていることから、その確率質量関数は\(f_X(x)= \frac{1}{6}\)、\(f_Y(y)= \frac{1}{6}\)です。
同時確率質量関数は、\(f_{X,Y}(x,y)=P(X=x, Y= y)= \frac{1}{6^2}\)となります。起こりうる結果の集合\(\Omega^2 =\Omega \times \Omega\)において、\(X=x\)かつ\(Y=y\)を満たす要素は\((x,y)\)の1つのみです。全事象は\(6^2\)個なので、確率は\(\frac{1}{6^2}\)となるわけですね。
よって、\(f_{X,Y}(x,y)=\frac{1}{6^2}=\frac{1}{6}\frac{1}{6} =f_{X}(x)f_Y(y)\)が成り立つので、独立です。
別の例として、サイコロを1回投げて偶数の目が出る回数を\(X\)、2が出る回数を\(Y\)としましょう。
\[X (\omega)= \begin{cases}1 & (\omega が偶数 )\\0 & (それ以外)\end{cases}\]
\[Y (\omega)= \begin{cases}1 & (\omega =2 )\\0 & (それ以外)\end{cases}\]
このとき、\(X,Y\)は独立ではありません。
それぞれの確率質量関数は、
\[f_X (x)= \begin{cases}\frac{1}{2} & (x が偶数 )\\ \frac{1}{2} & (それ以外)\end{cases}\]
\[f_Y (y)= \begin{cases}\frac{1}{6} & (y =2 )\\\frac{5}{6} & (それ以外)\end{cases}\]
となります。
一方、同時確率質量関数\(f_{X,Y}(x,y)=P(X=x, Y= y)\)について考えましょう。ひとつのサイコロを振っているので、\(x=y\)となる結果しかおきません。公平なサイコロなのでどれも同じ確率です。したがって、
\[f_{X,Y}(x,y)= \begin{cases}\frac{1}{6} & (x=y )\\0 & (それ以外)\end{cases}\]
となります。
確率質量関数の積は
\[f_X (x)f_Y(y)= \begin{cases}\frac{1}{12} & (y=2 )\\\frac{5}{12} & (それ以外)\end{cases}\]
となります。よって、例えば\(f_{X,Y}(2,2)=\frac{1}{6}\)、\(f_X(2)f_Y(2)= \frac{1}{12}\)となるので、独立ではありません。
連続確率変数
\(\Omega =[0,1]\times [0,1]\)、\(P\)として連続一様分布を考えましょう。
\(X,Y\)を一様分布に従う確率分布で、同時確率密度関数が
\[f_{X,Y}(x,y) = \begin{cases}1 & ((x,y)\in \Omega)\\0 & (それ以外)\end{cases}\]
であるとします。このとき、これらの確率変数は独立です。
なぜなら、\(X,Y\)の確率密度関数は
\[f_{X}(x) = \begin{cases}1 & (x \in [0,1])\\0 & (それ以外)\end{cases}\]
\[f_{Y}(y) = \begin{cases}1 & (y \in [0,1])\\0 & (それ以外)\end{cases}\]
なので、\(f_{X,Y}(x,y)=f_{X}(x)f_Y (y)\)が成り立つからです。
別の例として、確率変数\(X,Y\)の同時確率密度関数が
\[f_{X,Y}(x,y) = \begin{cases}x+y & ((x,y)\in \Omega)\\0 & (それ以外)\end{cases}\]
で、それぞれの確率密度関数がその周辺確率密度関数
\[f_{X}(x) = \begin{cases}x+\frac{1}{2} & (x\in [0,1])\\0 & (それ以外)\end{cases}\]
\[f_{Y}(y) = \begin{cases}y+\frac{1}{2} & (y\in [0,1])\\0 & (それ以外)\end{cases}\]
となるケースを考えましょう。このとき、\(X,Y\)は独立ではありません。
なぜなら、積を計算すると
\[f_{X}(x)f_Y(y) = \begin{cases}(x+\frac{1}{2})(y+\frac{1}{2}) & ((x,y)\in \Omega)\\0 & (それ以外)\end{cases}\]
となります。例えば、\(f_{X,Y}(0,0)=0\)、\(f_{X}(0)f_Y(0)=\frac{1}{4}\)と等しくないので、独立ではないことがわかりました。
性質
確率変数\(X,Y\)が独立ならば、次の性質が成り立つことが知られています。
- \(E(XY)=E(X)E(Y)\)
- \(V(X+Y) = V(X)+V(Y)\)
- \(\mathrm{Cov}(X,Y)=0\)
どれも独立という条件を外せば、一般には成り立ちません。
例えば独立ならば共分散が0になるという性質から、共分散が0でない2次元の正規分布に従う確率変数\(X,Y\)は独立ではありません。
また、この性質の逆は一般には成り立たないことに注意しましょう。共分散が0ではあるが、独立でない確率変数の例が存在することが知られています。これらの性質は、独立でないことを判定するためには使えますね。
以上、確率変数の独立性とは何か、具体例と性質を紹介してきました。
今回は2つの確率変数の独立性を紹介しましたが、同様にして複数の確率変数の独立性、確率変数族の独立性が定義できます。積の数をそのまま増やした形です。
\[f_{X}(x)=f_{X_{1}}(x_1)f_{X_2}(x_2)\cdots f_{X_{n}}(x_n)\]
独立で同じ分布に従う確率変数族、独立同分布の考え方は、統計的推測、サンプルによって母集団の性質を調べるための基礎となっています。
まずは2つの確率変数の具体例を通して、どんな例が独立でどんな例がそうでないのか、感覚的に理解すると良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥5,862 (中古品)