どうも、木村(@kimu3_slime)です。
今回は、Julia(Optim)で2変数関数の最小値・最大値を求める方法を紹介します。
準備
Optimを使うので、持っていなければインストールしておきましょう。
1 2 | using Pkg Pkg.add("Optim") |
準備として、以下のコードを実行しておきます。
1 | using Optim |
2変数関数の最小値・最大値を求める方法
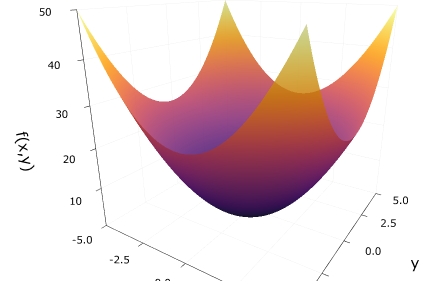
最初に、2変数関数
\[ f_1(x_1,x_2) =x_1 ^2 +x_2 ^2\]
の最小値を求めてみましょう。
「optimize(関数,初期値)」で、初期値を出発点として関数の最小値を探索した結果が得られます。
1 2 | f1(x) = x[1]^2 +x[2]^2 res = optimize(f1,[1.0,1.0]) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | * Status: success * Candidate solution Final objective value: 1.251398e-09 * Found with Algorithm: Nelder-Mead * Convergence measures √(Σ(yᵢ-ȳ)²)/n ≤ 1.0e-08 * Work counters Seconds run: 0 (vs limit Inf) Iterations: 31 f(x) calls: 63 |
「Candidate solution Final objective value:」が最小値です。今回の例ならば、1.251398e-09、すなわち\(10^{-9}\)と0に近い値が求まっています。
「Algorithm:」は探索に使ったアルゴリズムで、ネルダー・ミード法と呼ばれるものです。
最小値は「minimum(res)」、最小点(最小化点)は「Optim.minimizer(res)」で表示できます。
1 2 | minimum(res) Optim.minimizer(res) |
1 2 3 4 5 | 1.251397788593364e-9 2-element Vector{Float64}: 3.263668293377218e-5 -1.3647150459850139e-5 |
ネルダー・ミード法は微分の情報を使わない探索法なので、多少の誤差があるのが気になりますね。アルゴリズムとして、2次の微分を参照するニュートン法を指定してみましょう。
1 2 | res = optimize(f,[1.0,1.0], Newton()) Optim.minimizer(res) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | * Status: success * Candidate solution Final objective value: 0.000000e+00 * Found with Algorithm: Newton's Method * Convergence measures |x - x'| = 1.00e+00 ≰ 0.0e+00 |x - x'|/|x'| = Inf ≰ 0.0e+00 |f(x) - f(x')| = 2.00e+00 ≰ 0.0e+00 |f(x) - f(x')|/|f(x')| = Inf ≰ 0.0e+00 |g(x)| = 0.00e+00 ≤ 1.0e-08 * Work counters Seconds run: 0 (vs limit Inf) Iterations: 1 f(x) calls: 4 ∇f(x) calls: 4 ∇²f(x) calls: 1 |
1 2 3 | 2-element Vector{Float64}: 0.0 0.0 |
きれいに原点で最小値0を取ることがわかりました。
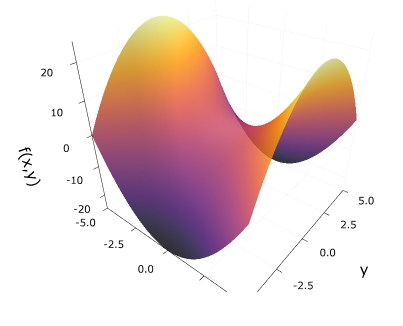
\(f_2(x_1,x_2) =x_1 ^2 -x_2 ^2 \)の最小値を調べてみましょう。
1 2 | f2(x) = x[1]^2 -x[2]^2 res = optimize(f2,[1.0,1.0], Newton()) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | * Status: failure (line search failed) * Candidate solution Final objective value: -8.843508e+110 * Found with Algorithm: Newton's Method * Convergence measures |x - x'| = 0.00e+00 ≤ 0.0e+00 |x - x'|/|x'| = 0.00e+00 ≤ 0.0e+00 |f(x) - f(x')| = 8.84e+110 ≰ 0.0e+00 |f(x) - f(x')|/|f(x')| = 1.00e+00 ≰ 0.0e+00 |g(x)| = 6.10e+59 ≰ 1.0e-08 * Work counters Seconds run: 0 (vs limit Inf) Iterations: 3 f(x) calls: 92 ∇f(x) calls: 92 ∇²f(x) calls: 3 |
探索は失敗し、最終値は負の方向に大きくなっていることがわかります。この関数に最小値(と最大値)は存在しません。
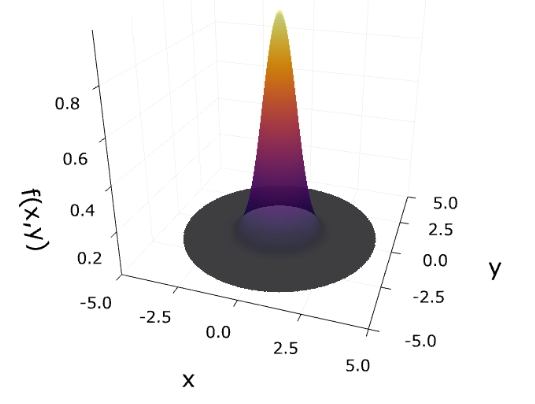
\(f_3 (x) = e^{-(x_1^2 +x_2 ^2)}\)の最大値を求めたいとしましょう。符号を反転させた\(-f_3\)の最小値を求めれば、最大値が求められます。
1 2 | f3(x) = -exp(-(x[1]^2 +x[2]^2)) res = optimize(f,[1.0,1.0],Newton()) |
1 2 | res = optimize(f3,[1.0,1.0],Newton()) Optim.minimizer(res) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | * Status: success * Candidate solution Final objective value: -1.000000e+00 * Found with Algorithm: Newton's Method * Convergence measures |x - x'| = 9.83e-07 ≰ 0.0e+00 |x - x'|/|x'| = 8.35e+05 ≰ 0.0e+00 |f(x) - f(x')| = 1.02e-12 ≰ 0.0e+00 |f(x) - f(x')|/|f(x')| = 1.02e-12 ≰ 0.0e+00 |g(x)| = 0.00e+00 ≤ 1.0e-08 * Work counters Seconds run: 0 (vs limit Inf) Iterations: 5 f(x) calls: 15 ∇f(x) calls: 15 ∇²f(x) calls: 5 2-element Vector{Float64}: -1.0951684996835008e-12 -1.1783642616071408e-12 |
最小値が\(-1\)となっているので、求めたい関数の最大値は\(1\)です。
与える関数と探索のアルゴリズムによって、得られる結果は変わります。
非常に粗いヒューリスティックとして
解析的な勾配とヘシアンを持つ低次元問題には、トラスト領域を持つニュートン法を使用します。より大きな問題や解析的なヘシアンがない場合は,LBFGSを使用し,必要に応じてパラメータmを調整します.関数が微分不可能な場合、Nelder-Meadを使用します。ロバスト性にはHagerZhangラインサーチを、スピードにはBackTrackingを使用します。
引用、DeepL:Algorithm choice – Optim.jl
公式マニュアルによると、関数の解析的な性質の良さに応じて、ニュートン法、LBFGS法、Nelder-Mead法を試すと良いようです。
少し複雑な例として、
\[ \begin{aligned}f_4 = \sqrt{x_1^2+x_2^2}(|\sin(x_1)|+1)\end{aligned} \]
の最小値を、各アルゴリズムで求めてみましょう。
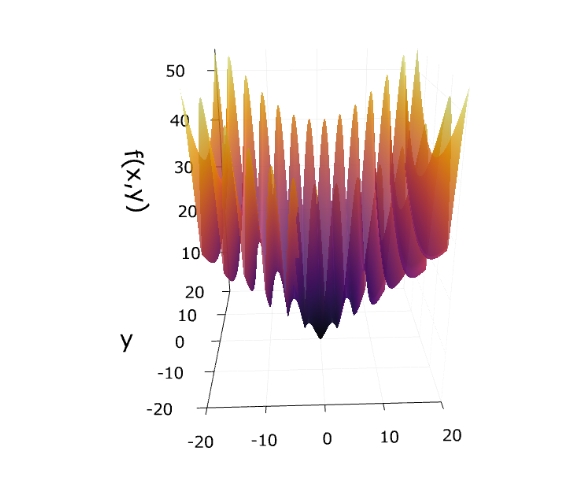
1 2 | optimize(f4 , [10.0,10.0], Newton()) Optim.minimizer(optimize(f4, [10.0,10.0], Newton())) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | * Status: success * Candidate solution Final objective value: 9.109913e-18 * Found with Algorithm: Newton's Method * Convergence measures |x - x'| = 3.43e-13 ≰ 0.0e+00 |x - x'|/|x'| = 3.88e+04 ≰ 0.0e+00 |f(x) - f(x')| = 3.54e-13 ≰ 0.0e+00 |f(x) - f(x')|/|f(x')| = 3.88e+04 ≰ 0.0e+00 |g(x)| = 1.46e-12 ≤ 1.0e-08 * Work counters Seconds run: 0 (vs limit Inf) Iterations: 22 f(x) calls: 96 ∇f(x) calls: 96 ∇²f(x) calls: 22 2-element Vector{Float64}: -8.840575375137535e-18 2.198802978582717e-18 |
1 2 | res = optimize(f4,[10.0,10.0], LBFGS()) Optim.minimizer(res) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | * Status: success * Candidate solution Final objective value: 4.466617e-14 * Found with Algorithm: L-BFGS * Convergence measures |x - x'| = 8.66e-10 ≰ 0.0e+00 |x - x'|/|x'| = 2.04e+04 ≰ 0.0e+00 |f(x) - f(x')| = 9.10e-10 ≰ 0.0e+00 |f(x) - f(x')|/|f(x')| = 2.04e+04 ≰ 0.0e+00 |g(x)| = 7.01e-09 ≤ 1.0e-08 * Work counters Seconds run: 1 (vs limit Inf) Iterations: 35 f(x) calls: 106 ∇f(x) calls: 106 2-element Vector{Float64}: -1.3834118121144328e-14 -4.2469797636904737e-14 |
1 2 | res = optimize(f4,[10.0,10.0],NelderMead()) Optim.minimizer(res) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | * Status: success * Candidate solution Final objective value: 1.256637e+01 * Found with Algorithm: Nelder-Mead * Convergence measures √(Σ(yᵢ-ȳ)²)/n ≤ 1.0e-08 * Work counters Seconds run: 0 (vs limit Inf) Iterations: 58 f(x) calls: 115 2-element Vector{Float64}: 12.566370614364185 0.0001331080824509482 |
ニュートン法、LBFGS法では、ほぼ原点で最小値0が得られています。一方、ネルダー・ミード法では、\(x_1= 4\pi\)付近の極小値が得られていて、大域的な最小値が得られませんでした。
調査した関数\(f_4\)は絶対値により微分不可能な点(直線)を持っていますが、それは例外的で、多くの点で2階微分が計算できるので、その情報を使った方が最適な値にたどり着けるようですね。
以上、Julia(Optim)で2変数関数の最小値・最大値を求める方法を紹介してきました。
微分の計算を自分で行わなくても、関数を与えるだけで最小値を求めてくれるので便利ですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Julia(Plotly)でグリグリ動かせる3Dグラフを作る方法
Julia(SymPy)で1変数関数の最大値最小値を求める方法