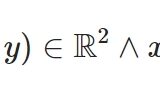どうも、木村(@kimu3_slime)です。
今回は、Julia(SymPy)で実数区間の開集合、閉集合、内部、閉包、境界、有界性を判定する方法を紹介します。
前提知識:Julia(SymPy)で数の集合(有限集合、整数、区間)の計算をする方法
準備
SymPyを使うので、持っていなければインストールしておきましょう。
1 2 | using Pkg Pkg.add("SymPy") |
準備として、以下のコードを実行しておきます。
1 | using SymPy |
開集合、閉集合
例として、次のような実数の区間を考えましょう。
1 2 3 4 5 6 | A1 = sympy.Interval(0,1) A2 = sympy.Interval.open(0,1) A3 = sympy.Interval.Ropen(0,1) A4 = sympy.Reals A5 = sympy.EmptySet A = [A1,A2,A3,A4,A5] |
\[ \begin{aligned}\left[ \begin{array}{r}\left[0, 1\right]\\\left(0, 1\right)\\\left[0, 1\right)\\\mathbb{R}\\\emptyset\end{array} \right]\end{aligned} \]
「集合.is_open」で開集合かどうか判定できます。
1 2 3 | for i in 1:5 display(A[i].is_open) end |
1 2 3 4 5 | false true false true true |
「集合.is_close」で閉集合かどうかの判定です。
1 2 3 | for i in 1:5 display(A[i].is_closed) end |
1 2 3 4 5 | true false false true true |
半開区間は開集合でも閉集合でもないこと、実数全体や空集合は開集合であり閉集合であることがわかりますね。
2次元以上のケースだと、開集合の判定ができないことがあります。
1 2 | sympy.Reals^2 (sympy.Reals^2).is_open |
\[ \begin{aligned}\mathbb{R}^{2}\end{aligned} \]
1 | true |
1 2 3 | @syms x y A7 = sympy.ConditionSet((x,y),Eq(x^2+y^2,1), sympy.Reals^2) A7.is_open |
\[ \begin{aligned}\left\{\left( x, \ y\right)\; \middle|\; \left( x, \ y\right) \in \mathbb{R}^{2} \wedge x^{2} + y^{2} = 1 \right\}\end{aligned} \]
1 | KeyError: key :is_open not found |
この例は、実際には閉集合であり、かつ開集合ではありません。
内部、閉包、境界
実数の区間に対し、その内部(interior)、閉包(closure)、境界(boundary)を求めることができます。
1 2 3 | for i in 1:5 display(A[i].interior) end |
\[ \begin{aligned}\left(0, 1\right)\end{aligned} \]
\[ \begin{aligned}\left(0, 1\right)\end{aligned} \]
\[ \begin{aligned}\left(0, 1\right)\end{aligned} \]
\[ \begin{aligned}\mathbb{R}\end{aligned} \]
\[ \begin{aligned}\emptyset\end{aligned} \]
開集合はその内部と一致しています。
1 2 3 | for i in 1:5 display(A[i].closure) end |
\[ \begin{aligned}\left[0, 1\right]\end{aligned} \]
\[ \begin{aligned}\left[0, 1\right]\end{aligned} \]
\[ \begin{aligned}\left[0, 1\right]\end{aligned} \]
\[ \begin{aligned}\mathbb{R}\end{aligned} \]
\[ \begin{aligned}\emptyset\end{aligned} \]
閉集合はその閉包と一致しています。
1 2 3 | for i in 1:5 display(A[i].boundary) end |
\[ \begin{aligned}\left\{0, 1\right\}\end{aligned} \]
\[ \begin{aligned}\left\{0, 1\right\}\end{aligned} \]
\[ \begin{aligned}\left\{0, 1\right\}\end{aligned} \]
\[ \begin{aligned}\emptyset\end{aligned} \]
\[ \begin{aligned}\emptyset\end{aligned} \]
内部と境界を合わせると、閉包になっていますね。
有界性
それぞれの区間が有界かどうか判定してみましょう。
「集合.inf」で下限、「集合.sup」で上限が求められます。
1 2 | A1.inf A1.sup |
\[ \begin{aligned}0\end{aligned} \]
\[ \begin{aligned}1\end{aligned} \]
与えられた区間が有界かどうか判定する関数を作ってみましょう。
1 2 3 4 5 6 7 8 9 | function is_bounded(A) if A == sympy.EmptySet println(A,"は有界") elseif (A.inf == -oo) || (A.sup == oo) println(A,"は非有界") else println(A,"は有界") end end |
下限が\(-\infty\)、または上限が\(\infty\)のケースが非有界、それ以外が有界です。
ただし、空集合に対してはsympyのinf,supが定義されていません。空真の考え方から、任意の実数が空集合の下限、上限であり、したがって空集合は有界集合と考えます。
1 2 3 | for i in 1:5 is_bounded(A[i]) end |
1 2 3 4 5 | Interval(0, 1)は有界 Interval.open(0, 1)は有界 Interval.Ropen(0, 1)は有界 Realsは非有界 EmptySetは有界 |
きちんと有界性が判定できていますね。
以上、Julia(SymPy)で実数区間の開集合、閉集合、内部、閉包、境界、有界性を判定する方法を紹介してきました。
無限個の区間(集合族)の共通部分、和集合も計算してみたいのですが、どうやらSymPyでは有限個の演算しかできないようです。
限界があるとはいえ、開集合や閉集合といった位相的な概念を記号的に判定できるのは嬉しいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)