どうも、木村(@kimu3_slime)です。
今回は、Julia(SymPy)でフーリエ級数を計算する方法を紹介します。
準備
SymPy, Plotsを使うので、持っていなければインストールしておきましょう。
1 2 3 | using Pkg Pkg.add("SymPy") Pkg.add("Plots") |
準備として、以下のコードを実行しておきます。
1 | using SymPy, Plots |
フーリエ級数を計算する方法
はじめに、記号として使う変数を用意しておきます。
1 | @vars x |
区間\([-\pi, \pi]\)における関数\(f\)のフーリエ級数展開は、
\[ \begin{aligned}f(x)=a_0 + \sum_{n=1}^\infty (a_n \cos nx +b_n \sin nx)\end{aligned} \]
\[ \begin{aligned}a_0=\frac{1}{2\pi} \int_{-\pi}^{\pi} f(x)dx\end{aligned} \]
\[ \begin{aligned}a_n=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x)\cos nxdx\end{aligned} \]
\[ \begin{aligned}b_n=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x)\sin nx dx\end{aligned} \]
と定義されます。
「sympy.fourier_series(関数,(x,範囲))」で特定の範囲における関数のフーリエ級数展開が求められます。
1 | sympy.fourier_series(x,(x,-PI, PI)) |
\[ \begin{aligned}2 \sin{\left(x \right)} – \sin{\left(2 x \right)} + \frac{2 \sin{\left(3 x \right)}}{3} + \ldots\end{aligned} \]
結果は無限級数であり、部分的に表示されています。
最初の0でない項を切り出して求めるには、「数式.truncate(n= 項数)」を使いましょう。
1 | sympy.fourier_series(x,(x,-PI, PI)).truncate(n= 5) |
\[ \begin{aligned}2 \sin{\left(x \right)} – \sin{\left(2 x \right)} + \frac{2 \sin{\left(3 x \right)}}{3}\\ – \frac{\sin{\left(4 x \right)}}{2} + \frac{2 \sin{\left(5 x \right)}}{5}\end{aligned} \]
「plot(関数)」を使えば、この結果のグラフを描くことができます。
1 | plot(sympy.fourier_series(x,(x,-PI, PI)).truncate(n= 5)) |
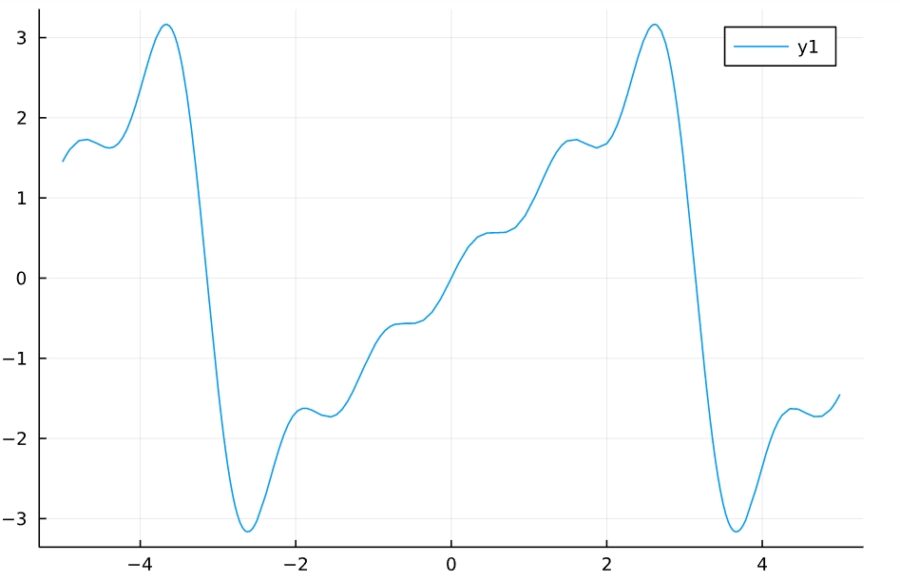
矩形波(ヘビサイド関数)について、同じことをやってみましょう。
1 2 | sympy.fourier_series(Heaviside(x),(x,-PI, PI)).truncate(n= 5) plot(sympy.fourier_series(Heaviside(x),(x,-PI, PI)).truncate(n= 5)) |
\[ \begin{aligned}\frac{2 \sin{\left(x \right)}}{\pi} + \frac{2 \sin{\left(3 x \right)}}{3 \pi} \\+ \frac{2 \sin{\left(5 x \right)}}{5 \pi} + \frac{2 \sin{\left(7 x \right)}}{7 \pi} + \frac{1}{2}\end{aligned} \]

ただし、その最初の第1項(定数関数)をプロットしようとすると、エラーが表示されていまいます。
1 2 | sympy.fourier_series(Heaviside(x),(x,-PI, PI)).truncate(n= 1) plot(sympy.fourier_series(Heaviside(x),(x,-PI, PI)).truncate(n= 1)) |
\[ \begin{aligned}\frac{1}{2}\end{aligned} \]
1 | #105 is not a Function, or is not defined at any of the values [-5.0, -1.0, 0.0, 0.01] |
Symの定数は、変数\(x\)を含んでいないので、plotの対象になってくれないようです。
定数関数を作り出すために、ヘビサイド関数の足し合わせ「Heaviside(x)+Heaviside(-x)」を利用します。最適な方法ではない気がしますが、これを使えば定数関数として扱ってくれます。
1 | plot(sympy.fourier_series(Heaviside(x),(x,-PI, PI)).truncate(n= 1)*(Heaviside(x)+Heaviside(-x))) |
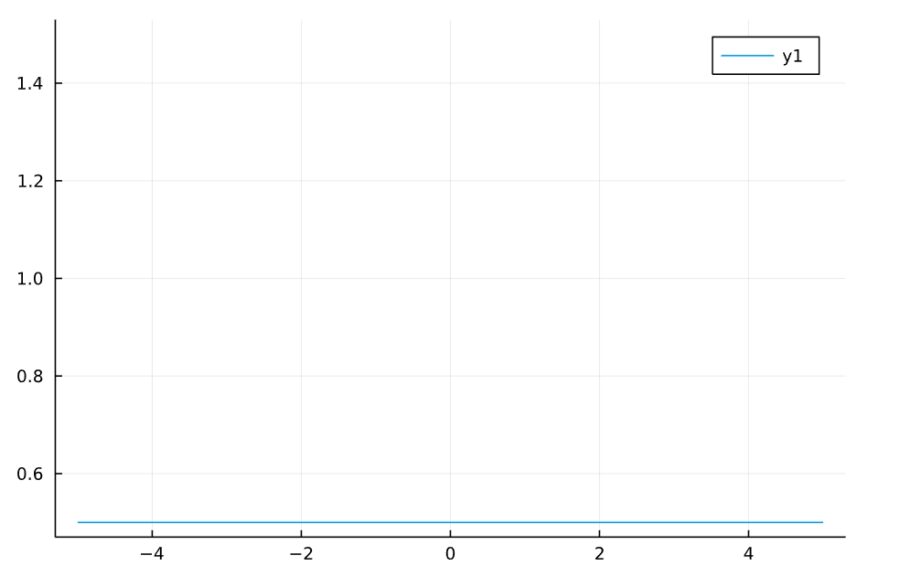
以上の結果をまとめて、与えられた関数のフーリエ級数展開のグラフを重ねて描く関数を作ってみましょう。
1 2 3 4 5 6 7 8 9 10 11 | function plot_fourier(f) p = plot(xlim=(-2*pi,2*pi),xticks=([-2pi,-pi, 0, pi, 2pi],["-2π", "-π", "0", "π","2π"])) plot!(f, label="f") (plot!(sympy.fourier_series(f,(x,-PI, PI)).truncate(n= 1) *(Heaviside(x)+Heaviside(-x)) , label=string(1) ) ) for i in 3:2:5 plot!(sympy.fourier_series(f,(x,-PI, PI)).truncate(n= i), label=string(i)) end plot!(sympy.fourier_series(f,(x,-PI, PI)).truncate(n= 100), label=string(100)) plot(p) end |
最初に「p」でプロットの土台を作り、その後「plot!」でグラフを重ねて書いていきます。最初は関数そのもの、続いてフーリエ級数展開1項、3項、5項、100項の順です。1項のみのケースが少し汚い式ですが、さきほど見た問題への対処をしています。
のこぎり波のフーリエ級数展開は次の通り。
1 | plot_fourier(x) |
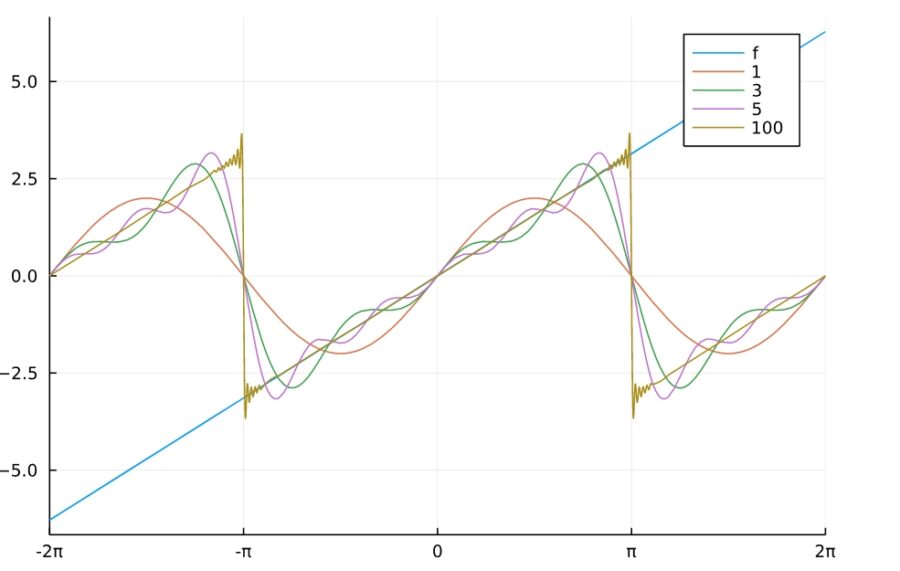
矩形波のフーリエ級数展開は次の通り。
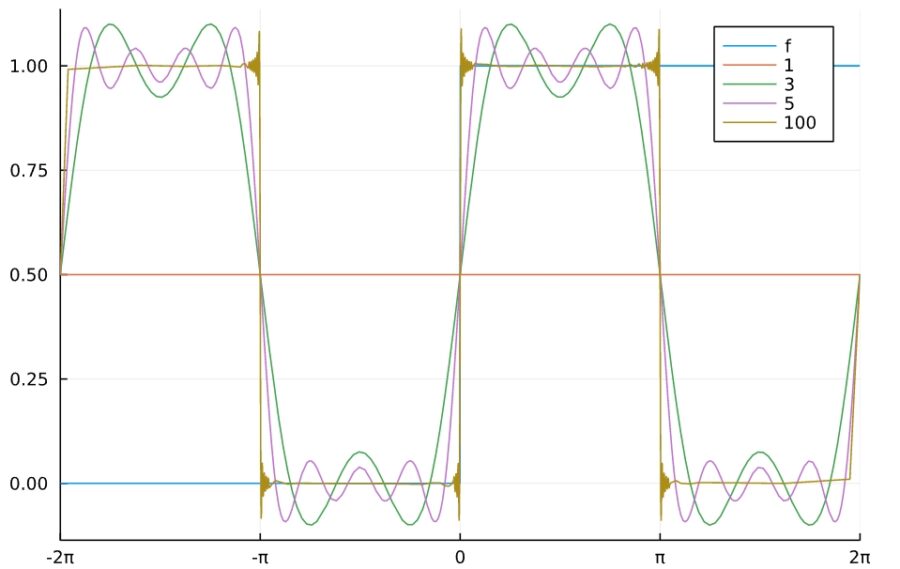
絶対サイン波のフーリエ級数展開は次の通り。
1 2 | sympy.fourier_series(abs(sin(x))).truncate(n= 5) plot_fourier(abs(sin(x))) |
\[ \begin{aligned}- \frac{4 \cos{\left(2 x \right)}}{3 \pi} – \frac{4 \cos{\left(4 x \right)}}{15 \pi} \\- \frac{4 \cos{\left(6 x \right)}}{35 \pi} – \frac{4 \cos{\left(8 x \right)}}{63 \pi} + \frac{2}{\pi}\end{aligned} \]
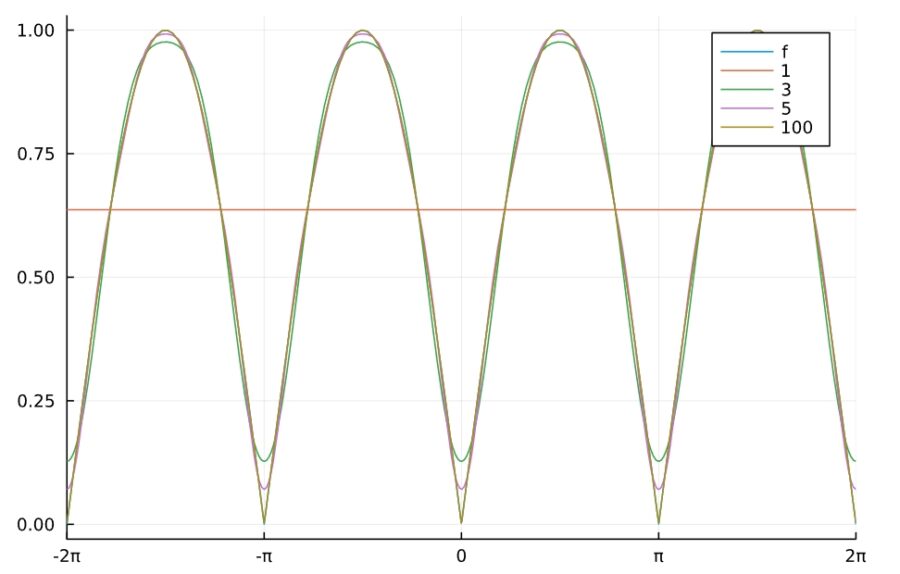
\(x^2\)のフーリエ級数展開は次の通り。
1 2 | sympy.fourier_series(x^2).truncate(n= 5) plot_fourier(x^2) |
\[ \begin{aligned}- 4 \cos{\left(x \right)} + \cos{\left(2 x \right)} – \frac{4 \cos{\left(3 x \right)}}{9}\\ + \frac{\cos{\left(4 x \right)}}{4} + \frac{\pi^{2}}{3}\end{aligned} \]
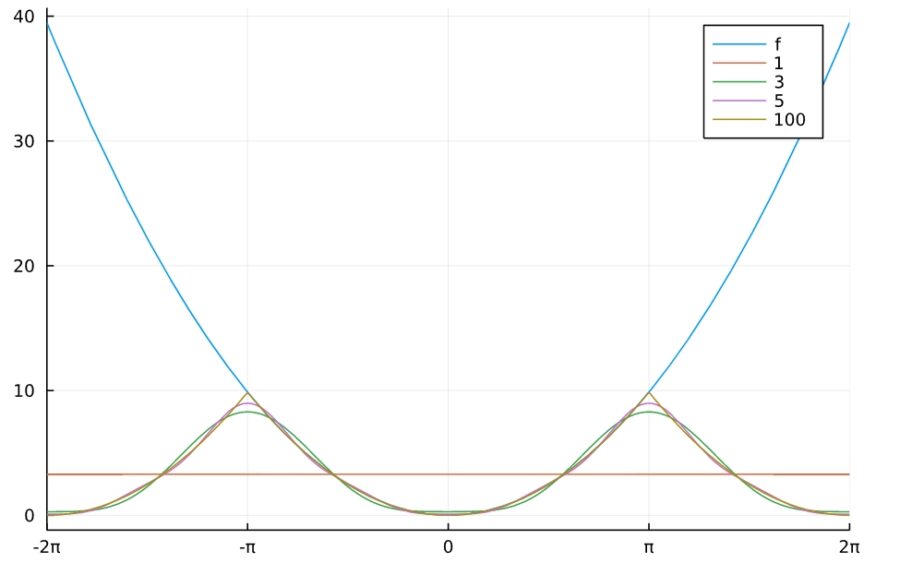
以上、Julia(SymPy)でフーリエ級数を計算する方法を紹介してきました。
以前Juliaで級数をプロットする方法で、フーリエ級数のプロットも紹介しましたが、そちらはフーリエ係数を手計算で導いた上で与えています。
SymPyを使うと、フーリエ係数の計算も込みで解いてくれるので、簡単ですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
矩形波とは:フーリエ級数展開の求め方、ギブス現象、ライプニッツの級数
Julia(SymPy)で数列の和、無限級数、べき級数を求める方法
Julia(SymPy)によるテイラー級数展開の求め方(指数対数、三角、双曲線)