どうも、木村(@kimu3_slime)です。
今回は、Julia(SymPy)でベクトルの計算、内積・ノルム・距離・角度、外積を計算する方法を紹介します。
準備
SymPyを使うので、持っていなければインストールしておきましょう。
1 2 | using Pkg Pkg.add("SymPy") |
準備として、以下のコードを実行しておきます。
1 | using SymPy |
Julia(SymPy)でベクトルの計算をする方法
ベクトルの用意
「Sym[1,2,2]」で、ベクトル\((1,2,2)\)を表すことができます。これは縦ベクトルです。
1 | Sym[1,2,2] |
\[ \begin{aligned}\left[ \begin{array}{r}1\\2\\2\end{array} \right]\end{aligned} \]
より一般に、文字を使ってベクトルを表しましょう。
1 2 3 4 | @vars a1 a2 a3 b1 b2 b3 c1 c2 c3 k a = Sym[a1,a2,a3] b= Sym[b1,b2,b3] c = Sym[c1,c2,c3] |
\[ \begin{aligned}\left[ \begin{array}{r}a_{1}\\a_{2}\\a_{3}\end{array} \right]\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{r}b_{1}\\b_{2}\\b_{3}\end{array} \right]\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{r}c_{1}\\c_{2}\\c_{3}\end{array} \right]\end{aligned} \]
和、スカラー倍
通常の和+、掛け算記号*を使うことで、ベクトルの和、スカラー倍が計算できます。
1 2 3 | a+b 2*a k*a |
\[ \begin{aligned}\left[ \begin{array}{r}a_{1} + b_{1}\\a_{2} + b_{2}\\a_{3} + b_{3}\end{array} \right]\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{r}2 a_{1}\\2 a_{2}\\2 a_{3}\end{array} \right]\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{r}a_{1} k\\a_{2} k\\a_{3} k\end{array} \right]\end{aligned} \]
\(-a\)は\(a\)の\(-1\)倍として解釈され、それは確かに\(a\)の(加法)逆ベクトルであることが確かめられます。
1 2 | -a a+(-a) |
\[ \begin{aligned}\left[ \begin{array}{r}- a_{1}\\- a_{2}\\- a_{3}\end{array} \right]\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{r}0\\0\\0\end{array} \right]\end{aligned} \]
内積・ノルム・距離・角度
ベクトル\(a,b\)の(ユークリッド)内積\(\langle a,b \rangle\)は、「a.dot(b)」で計算できます。
1 | a.dot(b) |
\[ \begin{aligned}a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}\end{aligned} \]
ベクトルのノルム(大きさ)\(\|a\|\)は、「a.norm()」です。
1 | a.norm() |
\[ \begin{aligned}\sqrt{\left|{a_{1}}\right|^{2} + \left|{a_{2}}\right|^{2} + \left|{a_{3}}\right|^{2}}\end{aligned} \]
距離\(d(a,b)=\|a-b\|\)は、関数が見つからなかったので、新たに定義しましょう。
1 2 3 4 5 | function dist(a,b) return (a-b).norm() end dist(a,b) |
\[ \begin{aligned}\sqrt{\left|{a_{1} – b_{1}}\right|^{2} + \left|{a_{2} – b_{2}}\right|^{2} + \left|{a_{3} – b_{3}}\right|^{2}}\end{aligned} \]
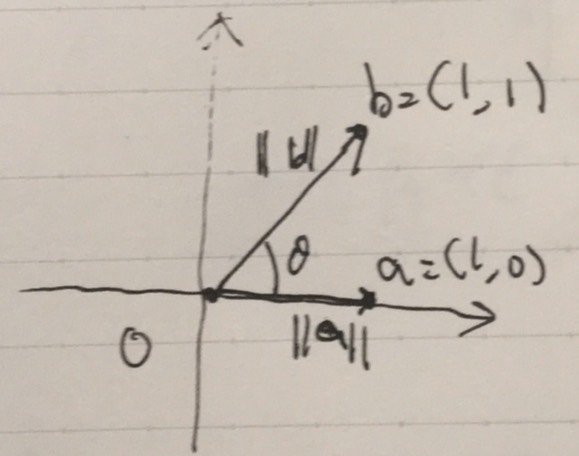
内積とノルムが計算できれば、ベクトルのなす角度
\[ \begin{aligned}\cos \theta =\frac{\langle a,b\rangle }{ \|a\| \|b\| }\end{aligned} \]
が求められます。これを\(\theta\)について解くために、逆三角関数acosを使います。
1 2 3 | function vectorangle(a,b) return acos(a.dot(b)/(a.norm()*b.norm())) end |
ベクトルの内積、ノルム、距離、なす角を、より具体的な例で計算してみましょう。
1 2 3 4 5 6 7 | x=Sym[1,0,0] y=Sym[1,1,0] x.dot(y) x.norm() y.norm() dist(x,y) vectorangle(x,y) |
\[ \begin{aligned}\left[ \begin{array}{r}1\\0\\0\end{array} \right]\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{r}1\\1\\0\end{array} \right]\end{aligned} \]
\[ \begin{aligned}1\end{aligned} \]
\[ \begin{aligned}1\end{aligned} \]
\[ \begin{aligned}\sqrt{2}\end{aligned} \]
\[ \begin{aligned}1\end{aligned} \]
\[ \begin{aligned}\frac{\pi}{4}\end{aligned} \]
\[ \begin{aligned}\langle ka+c,b\rangle = k\langle a,c\rangle+\langle c,b\rangle \end{aligned} \]
を確かめてみましょう。
1 2 3 | (k*a+c).dot(b) k*(a.dot(b))+c.dot(b) (k*a+c).dot(b) == k*(a.dot(b))+c.dot(b) |
\[ \begin{aligned}b_{1} \left(a_{1} k + c_{1}\right) + b_{2} \left(a_{2} k + c_{2}\right) + b_{3} \left(a_{3} k + c_{3}\right)\end{aligned} \]
\[ \begin{aligned}b_{1} c_{1} + b_{2} c_{2} + b_{3} c_{3} + k \left(a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}\right)\end{aligned} \]
false
素朴に両辺を「==」で比較すると、falseを返されてしまいます。SymPyでは「==」は数式が構造的に完全に等しいかチェックするもので、「\((x+1)^2\),\(x^2+2x+1\)」は等しくないものとして扱われています。
「expand(数式)」で両辺を展開すると、確かに等しいことがわかります。
1 | expand((k*a+c).dot(b)) == expand(k*(a.dot(b))+c.dot(b)) |
true
恒等式を確かめるには、左辺から右辺を引いて「simplify(数式)」で0に等しくなるか確かめる、という方法でも良いでしょう。
1 | simplify((k*a+c).dot(b) - (k*(a.dot(b))+c.dot(b))) |
\[ \begin{aligned}0\end{aligned} \]
外積
ベクトル\(a,b\)の外積(ベクトル積)\(a\times b\)は、「a.cross(b)」で計算できます。
1 | a.cross(b) |
\[ \begin{aligned}\left[ \begin{array}{r}a_{2} b_{3} – a_{3} b_{2}\\- a_{1} b_{3} + a_{3} b_{1}\\a_{1} b_{2} – a_{2} b_{1}\end{array}\right]\end{aligned} \]
外積\(a\times b\)ともとのベクトル\(a,b\)が直交していることが、計算で確かめられます。
1 2 | simplify(a.dot(a.cross(b))) simplify(b.dot(a.cross(b))) |
\[ \begin{aligned}0\end{aligned} \]
\[ \begin{aligned}0\end{aligned} \]
交代性
\[ \begin{aligned}a\times b = – b \times a\end{aligned} \]
が正しいかどうかも、チェックできます。
1 | a.cross(b) == -b.cross(a) |
true
ベクトル三重積の性質、ヤコビ恒等式
\[ \begin{aligned}a\times(b\times c)+b\times(c\times a)+c\times(a\times b)=0\end{aligned} \]
を確かめてみましょう。
左辺を計算して単純化しても、
1 | simplify(a.cross(b.cross(c))+b.cross(c.cross(a))+c.cross(a.cross(b))) |
\[ \begin{aligned}\left[ \begin{array}{r}a_{2} \left(b_{1} c_{2} – b_{2} c_{1}\right) – a_{3} \left(- b_{1} c_{3} + b_{3} c_{1}\right) + b_{2} \left(- a_{1} c_{2} + a_{2} c_{1}\right) – b_{3} \left(a_{1} c_{3} – a_{3} c_{1}\right) + c_{2} \left(a_{1} b_{2} – a_{2} b_{1}\right) – c_{3} \left(- a_{1} b_{3} + a_{3} b_{1}\right)\\- a_{1} \left(b_{1} c_{2} – b_{2} c_{1}\right) + a_{3} \left(b_{2} c_{3} – b_{3} c_{2}\right) – b_{1} \left(- a_{1} c_{2} + a_{2} c_{1}\right) + b_{3} \left(- a_{2} c_{3} + a_{3} c_{2}\right) – c_{1} \left(a_{1} b_{2} – a_{2} b_{1}\right) + c_{3} \left(a_{2} b_{3} – a_{3} b_{2}\right)\\a_{1} \left(- b_{1} c_{3} + b_{3} c_{1}\right) – a_{2} \left(b_{2} c_{3} – b_{3} c_{2}\right) + b_{1} \left(a_{1} c_{3} – a_{3} c_{1}\right) – b_{2} \left(- a_{2} c_{3} + a_{3} c_{2}\right) + c_{1} \left(- a_{1} b_{3} + a_{3} b_{1}\right) – c_{2} \left(a_{2} b_{3} – a_{3} b_{2}\right)\end{array}\right]\end{aligned} \]
なぜか単純化してくれません。
各成分ごとに単純化を行うと、
1 2 3 | simplify((a.cross(b.cross(c))+b.cross(c.cross(a))+c.cross(a.cross(b)))[1]) simplify((a.cross(b.cross(c))+b.cross(c.cross(a))+c.cross(a.cross(b)))[2]) simplify((a.cross(b.cross(c))+b.cross(c.cross(a))+c.cross(a.cross(b)))[3]) |
\[ \begin{aligned}0\end{aligned} \]
\[ \begin{aligned}0\end{aligned} \]
\[ \begin{aligned}0\end{aligned} \]
となって、恒等式が正しいことがわかります。
以上、Julia(SymPy)でベクトルの計算をする方法(内積・ノルム・距離・角度、外積)を紹介してきました。
具体的な数値だけでなく、記号を使って一般的な性質や恒等式を計算、チェックできるのは嬉しいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Juliaで1変数関数のグラフを描く方法(多項式、指数対数、三角関数)
Julia(SymPy)で1変数関数を積分する方法(多項式、指数対数、三角関数)
Julia(SymPy)で1変数関数を微分する方法(多項式、指数対数、三角関数)