どうも、木村(@kimu3_slime)です。
今回は、Julia(SymPy)によるテイラー級数展開の求め方(指数対数、三角、双曲線)を紹介します。
参考:なぜテイラー展開を学ぶ? 単振り子を例にわかりやすく解説、テイラー展開の展開式の覚え方、導き方、証明
準備
SymPyを使うので、持っていなければインストールしておきましょう。
1 2 | using Pkg Pkg.add("SymPy") |
準備として、以下のコードを実行しておきます。
1 | using SymPy |
テイラー級数展開の求め方
まず、\(x\)を数式処理用の変数、記号として用意しましょう。
1 | x=symbols("x") |
指数関数
「series(関数,級数)」で、\(x=0\)まわりでのテイラー級数展開(マクローリン展開)ができます。
1 | series(exp(x),x) |
\[ \begin{aligned}1 + x + \frac{x^{2}}{2} + \frac{x^{3}}{6} + \frac{x^{4}}{24} + \frac{x^{5}}{120} + O\left(x^{6}\right)\end{aligned} \]
\(O(x^6)\)は6次以降の項を表し、オーダーを表すランダウの記号と呼ばれるものです。
「series(関数,x,中心,次数)」で、中心や次数を変えることができます。指定しない場合、中心は\(x=0\)、次数は\(6\)以下とされています。
1 2 | series(exp(x),x,1) series(exp(x),x,0,10) |
\[ \begin{aligned}e + e \left(x – 1\right) + \frac{e \left(x – 1\right)^{2}}{2} + \frac{e \left(x – 1\right)^{3}}{6} \\+ \frac{e \left(x – 1\right)^{4}}{24} + \frac{e \left(x – 1\right)^{5}}{120} + O\left(\left(x – 1\right)^{6}; x\rightarrow 1\right)\end{aligned} \]
\[ \begin{aligned}1 + x + \frac{x^{2}}{2} + \frac{x^{3}}{6} + \frac{x^{4}}{24} + \frac{x^{5}}{120} \\+ \frac{x^{6}}{720} + \frac{x^{7}}{5040} + \frac{x^{8}}{40320} + \frac{x^{9}}{362880} + O\left(x^{10}\right)\end{aligned} \]
項数を変数\(n\)にして、一般的な展開
\[ \begin{aligned}e^{x} = \sum_{n=0}^\infty \frac{1}{n!}x^n\end{aligned} \]
が得られることを期待しましたが、
1 2 | n= symbols("n" ,integer=true) series(exp(x),x,0,n) |
結果はエラーでした。あくまで具体的な表示に限られるようですね。
Plotsを使うと、級数展開した結果をそのままグラフにすることができます。
新たに、「seriesplot」という、級数展開と元のグラフを描く関数を定義しましょう。
1 2 3 4 5 6 7 8 | function seriesplot(f) p=plot(xlim=(-1,1)) plot!(f,label= string(f)) for i in 1:5 plot!(series(f,x,0,i),label =string(i)) end plot(p) end |
指数関数で試すと、
1 | seriesplot(exp(x)) |
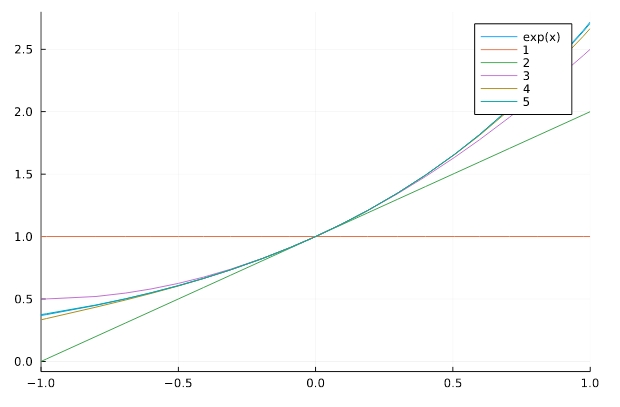
次数を増やすと、近似の精度がよくなっていることが見て取れます。
では、種々の初等関数をテイラー展開し、そのグラフを描いてみましょう。
対数関数、べき乗関数
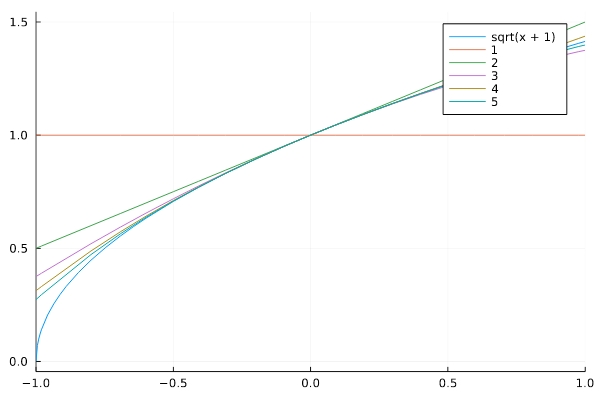
1 2 3 | a= symbols("a") series(log(1+x),x) series((1+x)^a,x) |
\[ \begin{aligned}1 + a x + \frac{a x^{2} \left(a – 1\right)}{2} + \frac{a x^{3} \left(a – 2\right) \left(a – 1\right)}{6}\\ + \frac{a x^{4} \left(a – 3\right) \left(a – 2\right) \left(a – 1\right)}{24} + \frac{a x^{5} \left(a – 4\right) \left(a – 3\right) \left(a – 2\right) \left(a – 1\right)}{120} + O\left(x^{6}\right)\end{aligned} \]

三角関数、逆三角関数
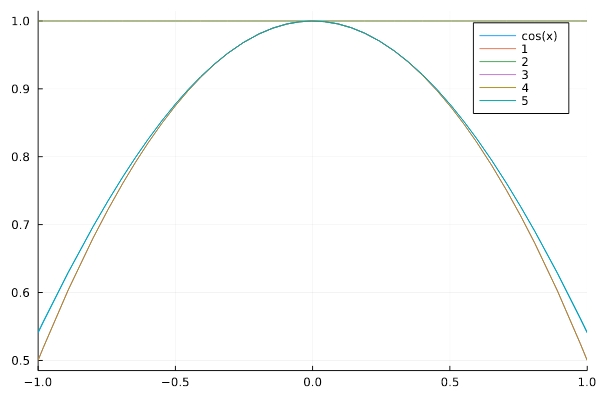
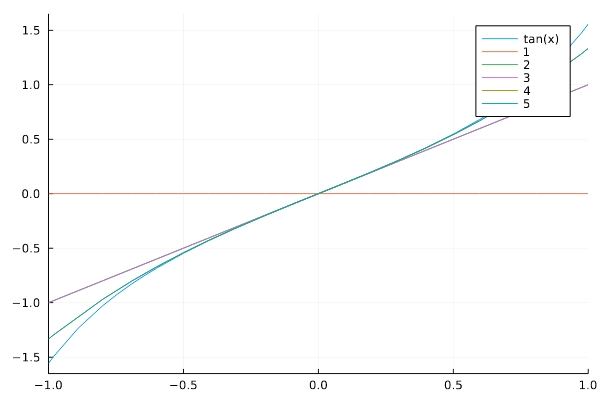
1 2 3 | series(sin(x),x) series(cos(x),x) series(tan(x),x) |
\[ \begin{aligned}1 – \frac{x^{2}}{2} + \frac{x^{4}}{24} + O\left(x^{6}\right)\end{aligned} \]
\[ \begin{aligned}x + \frac{x^{3}}{3} + \frac{2 x^{5}}{15} + O\left(x^{6}\right)\end{aligned} \]

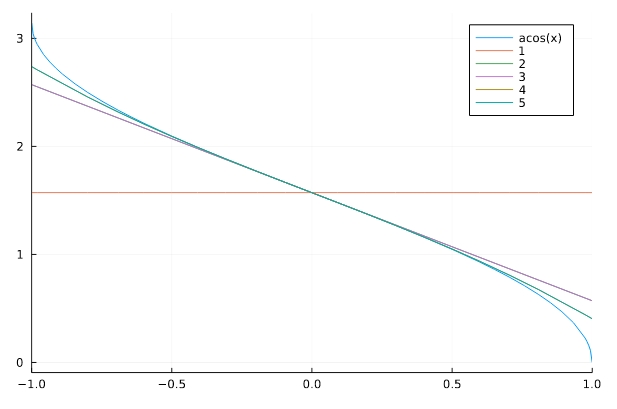
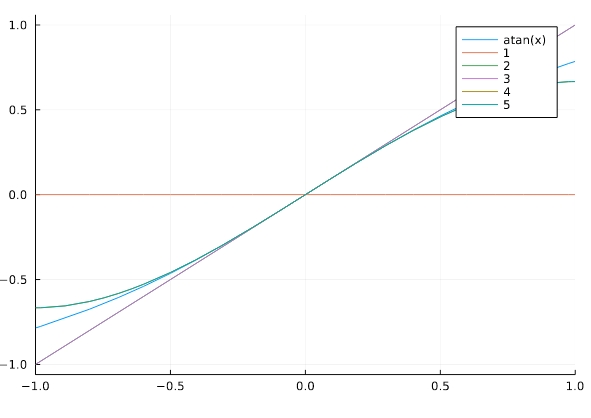
1 2 3 | series(asin(x),x) series(acos(x),x) series(atan(x),x) |
\[ \begin{aligned}x + \frac{x^{3}}{6} + \frac{3 x^{5}}{40} + O\left(x^{6}\right)\end{aligned} \]
\[ \begin{aligned}\frac{\pi}{2} – x – \frac{x^{3}}{6} – \frac{3 x^{5}}{40} + O\left(x^{6}\right)\end{aligned} \]
\[ \begin{aligned}x – \frac{x^{3}}{3} + \frac{x^{5}}{5} + O\left(x^{6}\right)\end{aligned} \]

双曲線関数、逆双曲線関数
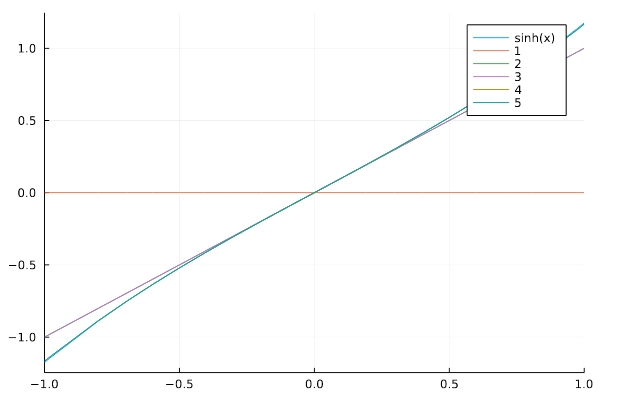
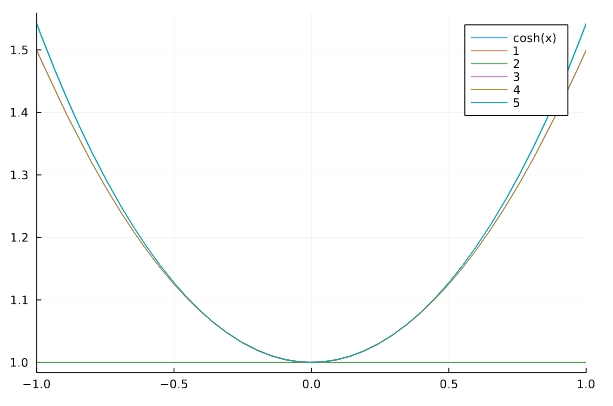
1 2 3 | series(sinh(x),x) series(cosh(x),x) series(tanh(x),x) |
\[ \begin{aligned}1 + \frac{x^{2}}{2} + \frac{x^{4}}{24} + O\left(x^{6}\right)\end{aligned} \]
\[ \begin{aligned}x – \frac{x^{3}}{3} + \frac{2 x^{5}}{15} + O\left(x^{6}\right)\end{aligned} \]
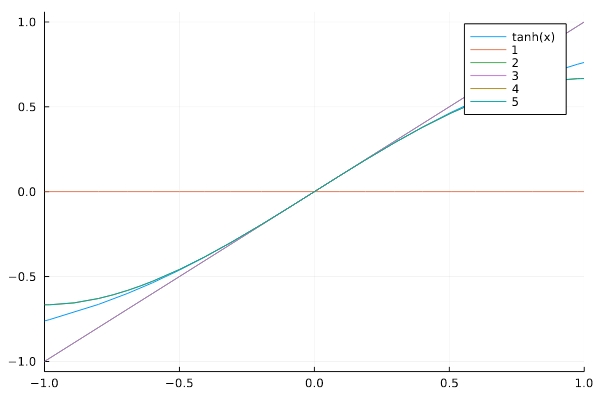
1 2 3 | series(asinh(x),x) series(acosh(2+x),x) series(atanh(x),x) |
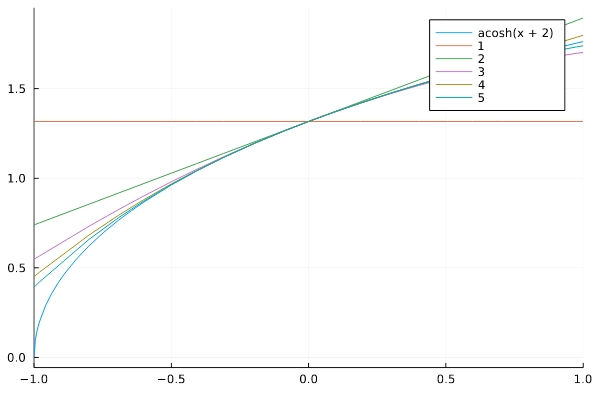
\(\mathrm{arccosh\,} (x)\)は、\(x\geq 1\)で定義されていることに注意。そこで\(x=2\)まわりの級数展開を考えました。
\[ \begin{aligned}x – \frac{x^{3}}{6} + \frac{3 x^{5}}{40} + O\left(x^{6}\right)\end{aligned} \]
\[ \begin{aligned}\operatorname{acosh}{\left(2 \right)} + \frac{\sqrt{3} x}{3} – \frac{\sqrt{3} x^{2}}{9} + \frac{\sqrt{3} x^{3}}{18}\\ – \frac{11 \sqrt{3} x^{4}}{324} + \frac{227 \sqrt{3} x^{5}}{9720} + O\left(x^{6}\right)\end{aligned} \]
\[ \begin{aligned}x + \frac{x^{3}}{3} + \frac{x^{5}}{5} + O\left(x^{6}\right)\end{aligned} \]

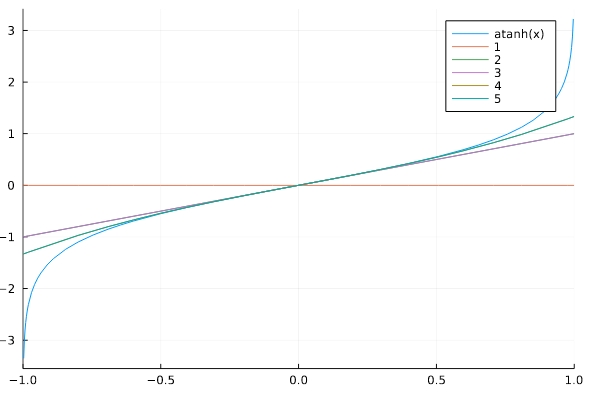
以上、Julia(SymPy)によるテイラー級数展開の求め方(指数対数、三角、双曲線)を紹介してきました。
微分を手計算してテイラー展開を求めるのは大変なので、コンピュータでも求められると嬉しいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Julia(SymPy)で1変数関数を積分する方法(多項式、指数対数、三角関数)
Julia(SymPy)で1変数関数を微分する方法(多項式、指数対数、三角関数)
.Julia(SymPy)で有理関数を部分分数分解、通分する方法
Julia(SymPy)で多項式の展開・因数分解、方程式を解く方法
Juliaで1変数関数のグラフを描く方法(多項式、指数対数、三角関数)