どうも、木村(@kimu3_slime)です。
今回は、Julia(Plots)で1変数関数のグラフを作る方法を紹介します。
準備
Plotsを使うので、持っていなければインストールしておきましょう。
1 2 | using Pkg Pkg.add("Plots") |
グラフを描く準備として、以下のコードを実行します。
1 | using Plots |
1変数関数のグラフ
1次関数
最初の例として、1次関数のグラフを描いてみましょう。
\[ \begin{aligned}f(x)=2x+1\end{aligned} \]
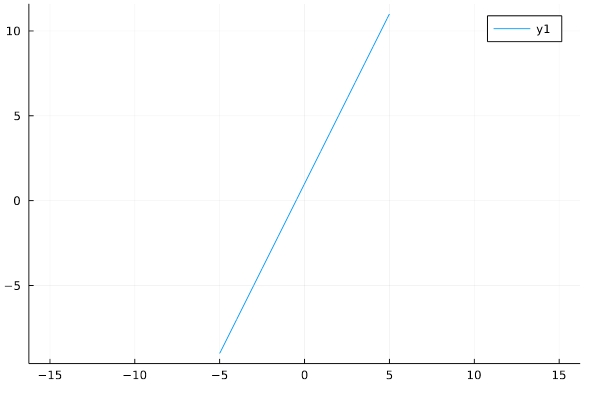
1 2 | f(x)=2*x+1 plot(f,aspect_ratio =1) |
掛け算は、アスタリスク「*」によって表す約束です。
「plot(f,aspect_ratio =1)」が、関数fのグラフを描く(プロットする)記述です。「aspect_ratio =1」は縦横比を1:1にするオプションで、これがないと2*xの傾きがわかりにくくなります。
この\(f\)に直交する直線
\[ \begin{aligned}g(x)= -\frac{1}{2} x+ 1\end{aligned} \]
のグラフを重ねて描いてみましょう。
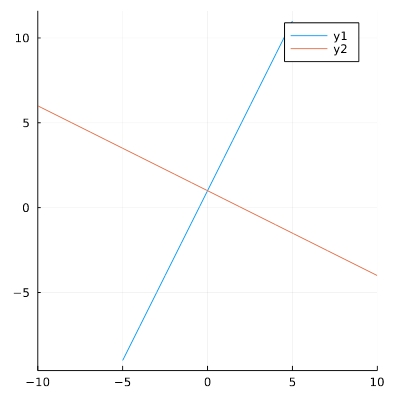
1 2 3 4 | f(x)=2*x+1 g(x)=-(1/2)*x+1 plot(f,aspect_ratio =1) plot!(g,aspect_ratio =1,xlims=(-10,10)) |
割り算は/を使い、例えば\(\frac{1}{2}\)を「1/2」と表します。
「plot!」によって、グラフを重ねて描いています。「!」をつけないと別々のグラフとしてプロットすることになるので。
また、オプションとして「xlims=(-10,10)」をつけました。これは描写する範囲を指定するのもので、\(x\)が-10以上10以下の範囲を描いています。指定しないとグラフが短くなりすぎたので、つけることにしました。「ylims」でy軸方向に描く範囲も指定できます。
他のグラフも、どんどん例示していきましょう。
2次関数、3次関数のグラフ
\[ \begin{aligned}f(x)= 3x^2 -1\end{aligned} \]
\[ \begin{aligned}f(x)= x^3-1\end{aligned} \]
1 2 | f(x)=3*x^2 -1 plot(f,aspect_ratio =1,xlim=(-1,1)) |
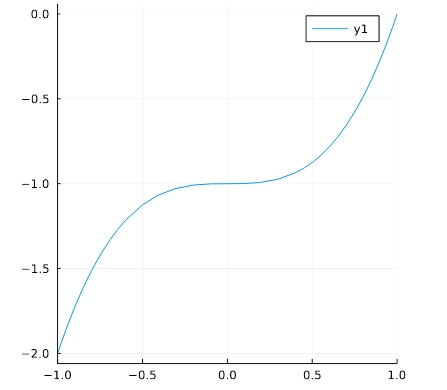
1 2 | f(x)=x^3 -1 plot(f,aspect_ratio =1,xlim=(-1,1)) |
手書きでは右上に書くべき乗の指数は、ハット「^」を使って表現します。例えば、\(3x^2\)は「3*x^2」です。

より高次の多項式関数も、同様にして描けます。
平方根やべき乗関数
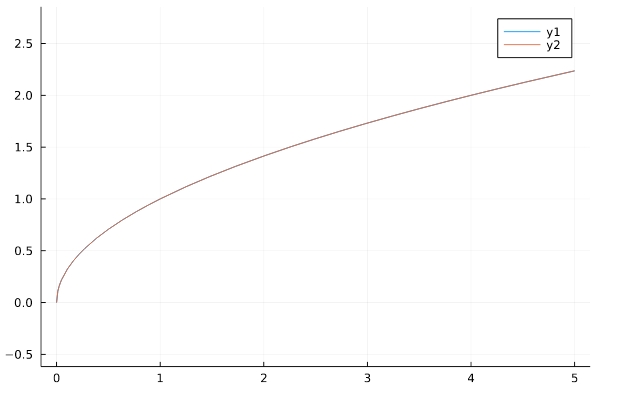
\(f(x)=\sqrt {x}=x^{\frac{1}{2}}\)
1 2 3 4 | f(x)=sqrt(x) g(x)=x^(1/2) plot(f,aspect_ratio =1) plot!(g) |
正の平方根を表す関数として、あらかじめ定義されている「sqrt(x)」を利用できます。
これは「x^(1/2)」と全く同じです。三乗根や四乗根、一般のケースも同様です。
反比例、分数関数
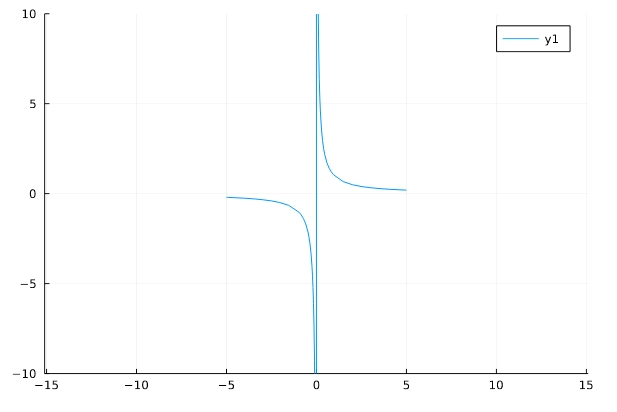
\(f(x)=\frac{1}{x}\)
1 2 | f(x)=1/x plot(f,aspect_ratio =1,ylim=(-10,10)) |
そのまま描こうとすると、\(x=0\)付近で妙なグラフになってしまいます。0割り算を含むグラフを描こうとしているからですね。
これを防ぐには、0を含まない範囲でグラフを書くか、関数の値が大きくなりすぎる(発散)する点の描写をやめることが有効です。
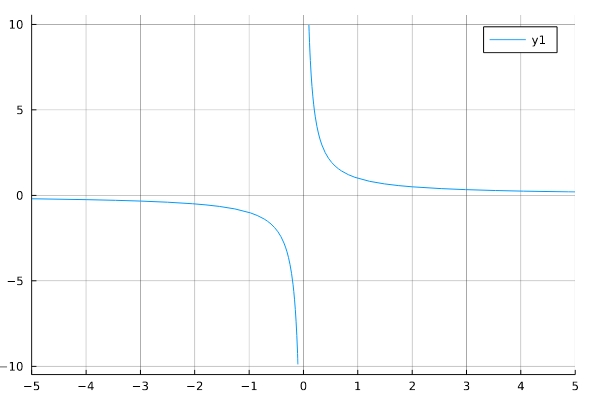
1 2 3 4 | trim(f ) = x -> abs(f(x)) > 10 ? NaN : f(x) f(x)=1/x plot(trim(f),xlim=(-5,5),xticks=(-5:5),gridalpha=0.7) |
「abs(f(x))」は\(f\)の絶対値\(|f(x)|\)です。trimという関数は、\(|f(x)|>10\)ならば何も描かない(NaN)、それ以下ならば\(f(x)\)を返すようになっています。これを使えば、無事に反比例のグラフを描くことができます。
漸近線をわかりやすくするため、plotのオプションを増やしました。「xticks=(-5:5)」は目盛りを増やし、「gridalpha=0.7」は罫線を濃く(最大で1)しています。
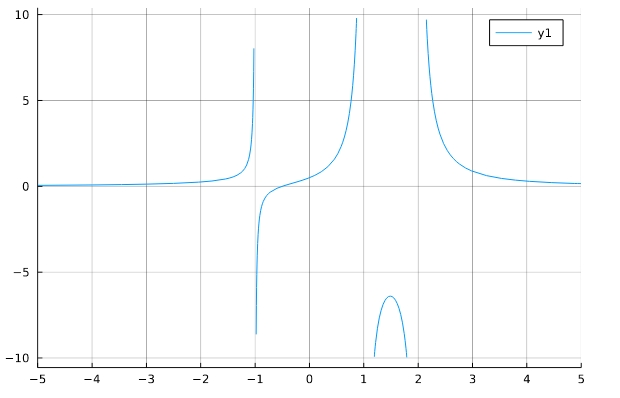
\[ \begin{aligned}f(x)=\frac{2x+1}{(x-2)(x-1)(x+1)}\end{aligned} \]
1 2 3 4 | trim(f ) = x -> abs(f(x)) > 10 ? NaN : f(x) f(x)=(2*x+1)/((x-2)*(x-1)*(x+1)) plot(trim(f),xlim=(-5,5),xticks=(-5:5),gridalpha=0.7) |
絶対値、床関数
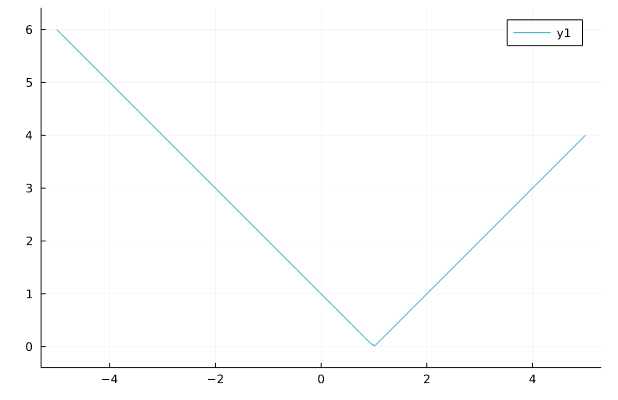
\(f(x)=|x-1|\)
1 2 | f(x)=abs(x-1) plot(f,aspect_ratio =1) |
絶対値関数\(|x|\)は、「abs(x)」によって表されます。
床関数(ガウス記号)
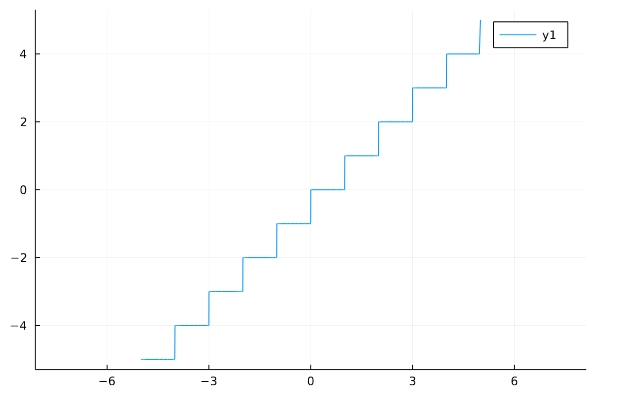
\[ \begin{aligned}f(x)= \lfloor x\rfloor\end{aligned} \]
1 2 | f(x)=floor(x) plot(f,aspect_ratio =1) |
床関数(ガウス記号)は、「floor(x)」です。天井関数は「ceil(x)」となります。
指数関数、対数関数
オイラー数\(e\)を底とする指数関数、(自然)対数関数
\[ \begin{aligned}f(x)=e^x\end{aligned} \]
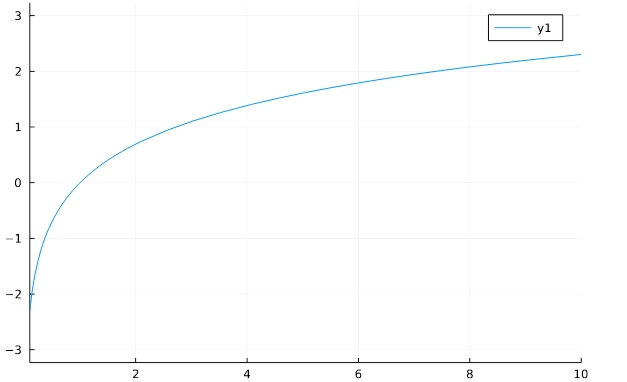
\[ \begin{aligned}f(x)= \log _e x\end{aligned} \]
1 2 | f(x)=exp(x) plot(f,aspect_ratio =1,xlim=(-1,1)) |
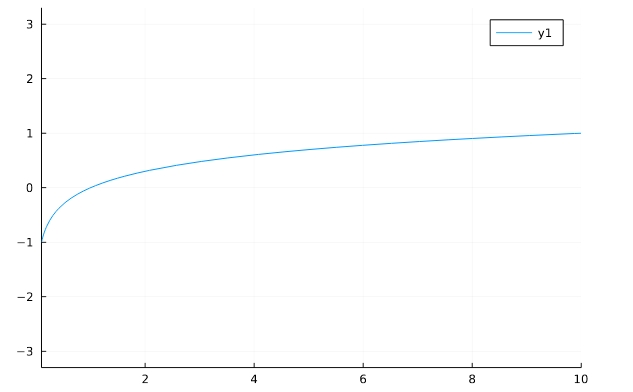
1 2 | f(x)=log(x) plot(f,aspect_ratio =1,xlim=(0.1,10)) |
指数関数はそのまま「e^x」と書いても使えないことに注意。指数関数(exponential)の頭文字を使った「exp(x)」を使います。

底を\(e\)以外にするとき
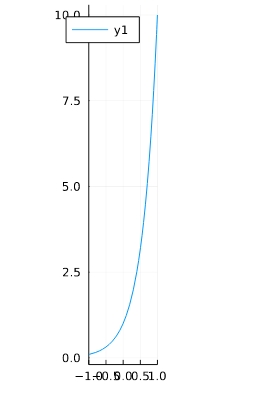
\[ \begin{aligned}f(x)=10^x\end{aligned} \]
\[ \begin{aligned}f(x)=\log_{10}x\end{aligned} \]
1 2 | f(x)=10^x plot(f,aspect_ratio =1,xlim=(-1,1)) |
1 2 | f(x)=log(10,x) plot(f,aspect_ratio =1,xlim=(0.1,10)) |
指数の場合は、「^」を使って書けば良いです。対数の場合は、「log(底,x)」という書き方になります。ただし、特に底が2,10のケースでは、「log2(x)」「log10(x)」という名前のついた関数もあります。
三角関数、逆三角関数
三角関数は、「sin(x)」のように書くことで表現できます。
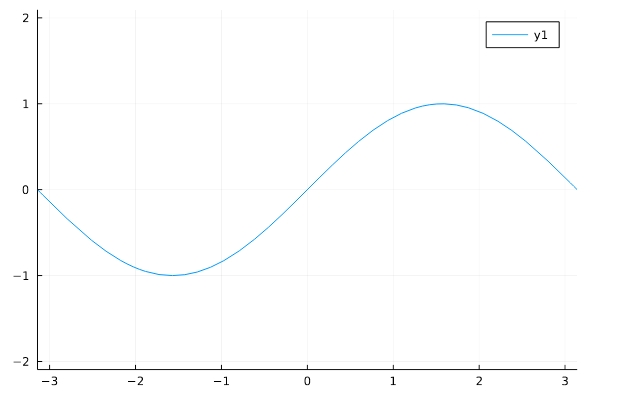
\[ \begin{aligned}f(x)=\sin x\end{aligned} \]
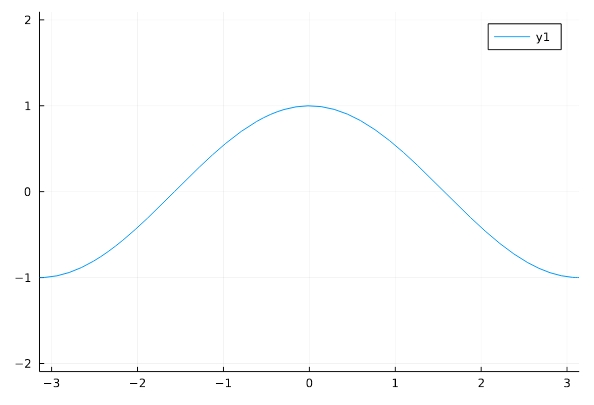
\[ \begin{aligned}f(x)=\cos x\end{aligned} \]
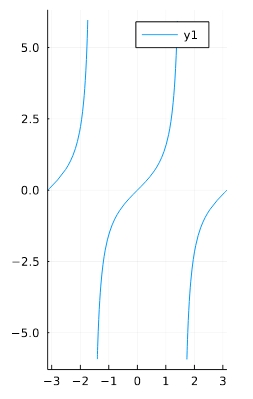
\[ \begin{aligned}f(x)=\tan x\end{aligned} \]
1 2 | f(x)=sin(x) plot(f,aspect_ratio =1,xlim=(-pi,pi)) |
1 2 | f(x)=cos(x) plot(f,aspect_ratio=1,xlim=(-pi,pi)) |
1 2 3 | trim(f ) = x -> abs(f(x)) > 6 ? NaN : f(x) f(x)=tan(x) plot(trim(f),aspect_ratio=1,xlim=(-pi,pi)) |
ただし、タンジェントでは\(\frac{1}{x}\)と同様、発散する点での問題が起こります。描く範囲を調整しましょう。
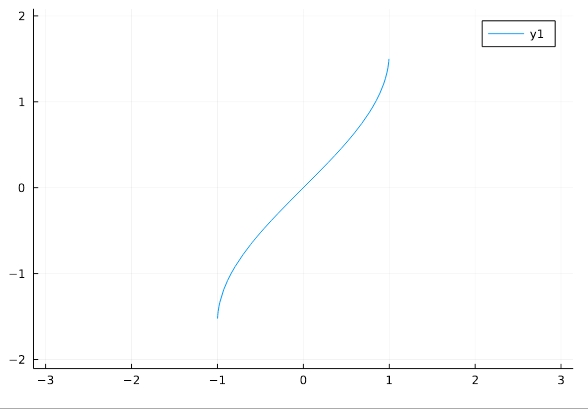
\[ \begin{aligned}f(x)= \mathrm{arcsin\,}x\end{aligned} \]
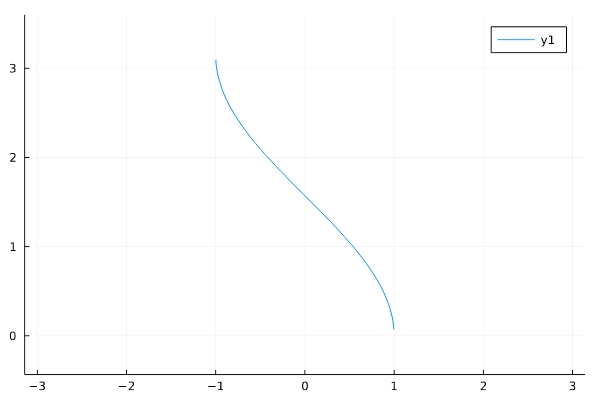
\[ \begin{aligned}f(x)= \mathrm{arccos\,}x\end{aligned} \]
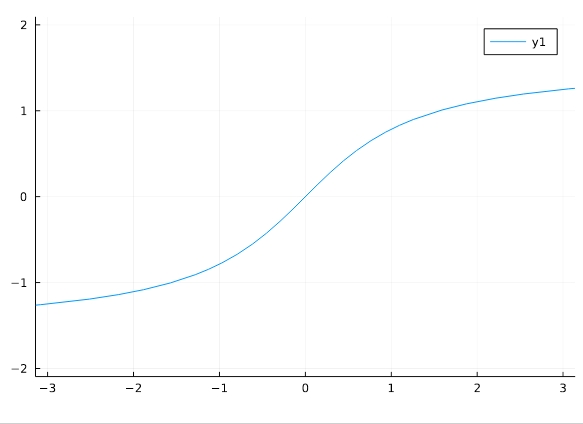
\[ \begin{aligned}f(x)= \mathrm{arctan\,}x\end{aligned} \]
1 2 | f(x)=asin(x) plot(f,aspect_ratio =1,xlim=(-pi,pi)) |
1 2 | f(x)=acos(x) plot(f,aspect_ratio =1,xlim=(-pi,pi)) |
1 2 | f(x)=atan(x) plot(f,aspect_ratio =1,xlim=(-pi,pi)) |
逆三角関数は、頭文字aだけつけて「asin(x)」といったように表せます。
双曲線関数、逆双曲線関数
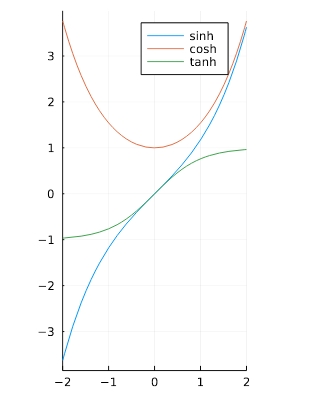
双曲線関数、逆双曲線関数も、三角関数と同様の方法で描けます。重ねて描いてみましょう。
1 2 3 4 5 6 | f(x)=sinh(x) g(x)=cosh(x) h(x)=tanh(x) plot(f,aspect_ratio =1,xlim=(-2,2),label="sinh") plot!(g,aspect_ratio =1,xlim=(-2,2),label="cosh") plot!(h,aspect_ratio =1,xlim=(-2,2),label="tanh") |
「label=”ラベル名”」で、右上に表示されるラベルの名前を指定できます。
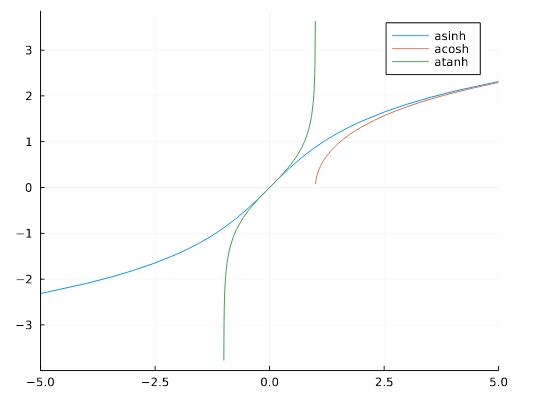
1 2 3 4 5 6 | f(x)=asinh(x) g(x)=acosh(x) h(x)=atanh(x) plot(f,aspect_ratio =1,xlim=(-5,5),label="asinh") plot!(g,aspect_ratio =1,xlim=(-5,5),label="acosh") plot!(h,aspect_ratio =1,xlim=(-5,5),label="atanh") |
以上、Juliaで1変数関数のグラフを描く方法を紹介してきました。
2変数関数のグラフ、ベクトル場については別記事で紹介しています。
関数は代数的な式としてだけでなく、グラフと結びつけて理解すると良いので、ぜひこの方法でいろいろ描いてみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Julia(Plotly)でグリグリ動かせる3Dグラフを作る方法
Julia(PyPlot)で2次元のベクトル場・流線を描く方法