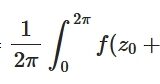どうも、木村(@kimu3_slime)です。
今回は、複素解析におけるポアソンの積分公式とは何か、ポアソン核とのを紹介します。
ポアソンの積分公式(Poisson’s integral formula)
極座標表示した2変数関数\(u(r,\theta)\)が円盤\(r<R\)における調和関数で、境界\(r=R\)で連続とする。このとき、\[ \begin{aligned}u(r,\theta) \\= \frac{1}{2\pi}\int_0 ^{2\pi} u(R,\phi) \frac{R^2 -r^2}{R^2-2rR\cos(\theta -\phi)+r^2} d\phi\end{aligned} \]
が成り立つ。
\(f(z)\)を同様の領域で正則な関数とすると、その実部\(u\)は調和関数で、同じ等式が成り立つ。
証明は、正則関数\(f(z)\)を考え、コーシーの積分公式\(f(z_0) =\frac{1}{2\pi i}\int_c \frac{f(z)}{z-z_0}dz\)を極座標で整理し、実部を取って得られるものです。詳しい証明は「Advanced Engineering Mathematics」を参照。
ポアソンの積分公式は、何が嬉しいのでしょうか。右辺の積分(ポアソン積分 Poisson integral)
\[ \begin{aligned}\int_0 ^{2\pi} u(R,\phi) \frac{R^2 -r^2}{R^2-2rR\cos(\theta -\phi)+r^2} d\phi\end{aligned} \]
は複雑で、具体的に計算するのは難しいです。
しかし、この積分の値は、関数の境界での値\(u(R,\phi)\)のみによって決まっていることが重要です。調和関数の円盤内部での値\(u(r,\theta)\)は、必ず境界\(u(R, \phi)\)での値から定まる積分と一致します。
逆に、
\[ \begin{aligned}\Delta u = 0 \quad( r <R)\\ u = g(\theta ) \quad( r =R)\end{aligned} \]
というラプラス方程式のディリクレ境界値問題を考えましょう。円盤の境界で与えられた関数\(g\)に対して、そこで一致して内部では調和な関数を求めたい、という問題です。
その解は、ポアソンの積分公式
\[ \begin{aligned}u(r,\theta)\\:= \frac{1}{2\pi}\int_0 ^{2\pi} g(\phi) \frac{R^2 -r^2}{R^2-2rR\cos(\theta -\phi)+r^2} d\phi\end{aligned} \]
によって与えられることが知られています。(例えば、Evans「Partial Differential Equations」を参照してください。)
積分を少し整理しましょう。
\[ \begin{aligned}P_r (\theta): = \frac{1}{2\pi} \frac{R^2 -r^2}{R^2-2rR\cos\theta +r^2}\end{aligned} \]
を円盤におけるポアソン核(Poisson’s kernel)と呼びます。t特に単位円盤\(R=1\)のケースを考えることが多いようです。
ポアソン核を使えば、積分は\(g\)との畳込みによって、
\[ \begin{aligned}u(r,\theta) = \int _0 ^{2\pi }g(\phi) P_r (\theta-\phi)d\phi \\ = (g*P_r )(\theta) \end{aligned} \]
と表せます。ラプラス方程式の円盤における境界値問題の解は、ポアソン核と境界での関数との畳み込みで表せる、と考えるシンプルです。
今回は2次元で円盤でのケースを考えていますが、一般の次元や領域でもポアソン核との畳込みで解が表せることが知られています。
特に円盤における問題では、積分公式をフーリエ級数の形で表せることが知られています。
\[ \begin{aligned}u(r,\theta) \\ =a_0 +\sum_{n=1}^\infty(\frac{r}{R})^n (a_n \cos n\theta +b_n \sin n\theta)\end{aligned} \]
\[ \begin{aligned}a_n =\frac{1}{\pi} \int_0^{2\pi} u(R,\phi)\cos n\phi d\phi\end{aligned} \]
\[ \begin{aligned}b_n =\frac{1}{\pi} \int_0^{2\pi} u(R,\phi)\sin n\phi d\phi\end{aligned} \]
(等比級数の和の公式を使う。証明は「Advanced Engineering Mathematics」を参照してください)
特に\(r= R\)のときは、
\[ \begin{aligned}u(R,\theta) \\ =a_0 +\sum_{n=1}^\infty (a_n \cos n\theta +b_n \sin n\theta)\end{aligned} \]
で、フーリエ級数展開そのものです。
つまり、境界で\(g(\theta)\)という値を持つ調和関数\(u\)を求めたいときに、\(g\)をフーリエ級数展開して係数を求めれば、それによって\(u\)を求められる、というわけです。
以上、複素解析におけるポアソンの積分公式とは、ポアソン核との関連を紹介してきました。
ポアソンの積分公式を考えるモチベーションとしては、ラプラス方程式の境界値問題を考えるとわかりやすいと思います。調和関数の内部での値は、実は境界での値から決まっている、という結果は強力ですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Kreyszig, E: Advanced Engineering Mathematics
Wiley John + Sons (2011-05-03T00:00:01Z)
¥10,314 (中古品)
岩波書店 (2003-12-12T00:00:01Z)
¥2,640
日本評論社 (2009-06-01T00:00:01Z)
¥5,170
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740
Partial Differential Equations (Graduate Studies in Mathematics)
Amer Mathematical Society (2010-04-02T00:00:01Z)
¥14,347 (中古品)
こちらもおすすめ
コーシーの積分公式とは、計算例と応用(無限回微分可能、コーシーの不等式)