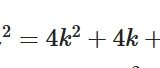どうも、木村(@kimu3_slime)です。
今回は、同軸円筒領域、円環領域におけるポテンシャル、2次元ラプラス方程式の解き方を紹介します。
同軸円筒(coaxial cylinder)は、2つの円筒で、外側の円の中心と内側の円の中心が一致しているものです。同心円筒とも。
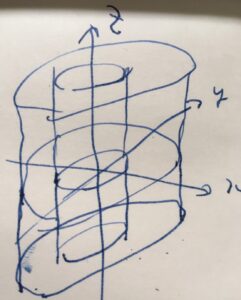
平面上に図示すると、次のようになります。内側の円の半径を\(r_1\)、外側を\(r_2\)としましょう。

このような穴の空いた円盤は、円環領域(アニュラス)と呼ばれるものです。
この2次元の領域における(電気)ポテンシャル、すなわちラプラス方程式
\[ \begin{aligned}\Delta u =\frac{\partial^2 u }{\partial x^2}+\frac{\partial^2 u }{\partial y^2}=0\end{aligned} \]
の解を求めてみましょう。円筒座標系の問題において、解が\(z\)に依存しない、\(z\)について一様なケースです。
これは同軸円筒形の2つのコンデンサーがあって、その電位差を求める問題とも言えます。
ラプラシアンは回転不変であることが知られており、\(u=u(r)\)という形の球対称な解を持つのではないかと推測できます。
そこで、考えている領域に合わせて、2次元極座標でのラプラシアン
\Delta u&= \frac{\partial^2 u}{\partial r^2} +\frac{1}{r} \frac{\partial u}{\partial r}+\frac{1}{r^2}\frac{\partial^2 u}{\partial \theta^2}
\
を用いましょう。\(u\)が球対称、\(r\)のみに依存して\(\phi\)に依存しないものを考えているので、
\[ \begin{aligned} \frac{\partial^2 u}{\partial r^2} +\frac{1}{r} \frac{\partial u}{\partial r}=0\end{aligned} \]
となります。変数は\(r\)のみなので、これらは常微分であり、整理すれば
\[ \begin{aligned}\frac{u^{\prime \prime}}{u^{\prime}} = -\frac{1}{r}\end{aligned} \]
です。これは変数分離形なので、積分によって解くことができ、
\[ \begin{aligned}\log u^{\prime} =-\log r+C_1\end{aligned} \]
\[ \begin{aligned}u^{\prime}= C_2 \frac{1}{r}\end{aligned} \]
\[ \begin{aligned}u(r) =C_3\log r +C_4\end{aligned} \]
と表すことができました。
これは対数ポテンシャル(logarithmic potential)と呼ばれています。2次元特有の形で、3次元以上では負のべき乗\(\frac{1}{r^{n-2}}\)が登場します。
具体的に、\(r_1=1\)、\(u(r_1)=0\)、\(r_2 =e\)、\(u(r_2)=10\)としたときの解を考えてみましょう。
\(u(1)=0\)から\(C_4=0\)です。\(u(e)=10\)から、\(C_3=10\)です。よって、
\[ \begin{aligned}u(r)=10 \log r\end{aligned} \]
となりました。3Dグラフで図示すると、次の通り。
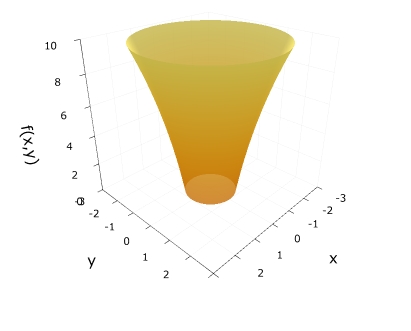
等高線\(u=c\)は、球対称な解なので当然ですが、同心円状となります。
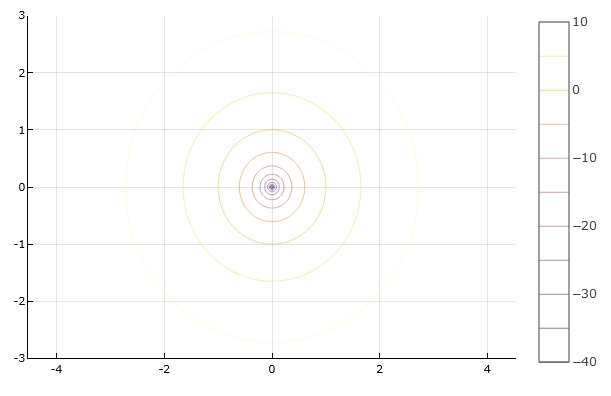
以上、同軸円筒領域におけるポテンシャル、2次元ラプラス方程式の解き方を紹介してきました。
円筒形の問題は基本的なので、具体的に計算してイメージを持っておくと良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Kreyszig, E: Advanced Engineering Mathematics
Wiley John + Sons (2011-05-03T00:00:01Z)
¥10,314 (中古品)
岩波書店 (2003-12-12T00:00:01Z)
¥2,640
日本評論社 (2009-06-01T00:00:01Z)
¥5,170
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740
こちらもおすすめ
逆二乗力(重力場、電磁場)のポテンシャルがラプラス方程式を満たすことの証明