どうも、木村(@kimu3_slime)です。
今回は、ローラン展開とは何か、その求め方、孤立特異点の分類について紹介します。
ローラン展開、孤立特異点とは
\(f\)をある領域において正則な関数とすると、それはテイラー展開できるのでした。
\[ \begin{aligned}f(z)= \sum_{n=0}^\infty a_n (z-z_0)^n\end{aligned} \]
しかし、\(f(z)= \frac{1}{z}\)のような関数を考えると、それは\(z=0\)において正則でなく、テイラー展開することはできません。そこで諦めるのでなく、少し「展開」の考え方を広げてみましょう。その都合の悪い点を除外した領域、例えば\(0<|z|< 1\)においては、
\[ \begin{aligned}f(z)= z^{-1}\end{aligned} \]
と\(z\)の負のべき乗で表せています。より一般に、負のべき乗(整数乗)を許容した級数展開が、ローラン展開(Laurent series)です。
\(f\)を円環領域(アニュラス)\(0<|z-z_0|<R\)において正則な関数とする。このとき、
\[ \begin{aligned} & f(z)\\&=\cdots + \frac{a_{-2}}{(z-z_0)^2}+ \frac{a_{-1}}{z-z_0}\\&+a_0 +a_1(z-z_0)+a_2(z-z_0)^2+\cdots \\ &=\sum_{n=-\infty}^\infty a_n(z-z_0)^n\end{aligned} \]
と\(0<|z-z_0|<R\)において級数展開できる。中心と領域の選び方を決めれば、この表示は一意的である。これを\(f\)のローラン展開と呼ぶ。
証明は神保「複素関数入門」やKreyszig「Advanced Engineering Mathematics」を参照してください。
\(f(z)=\frac{1}{z(z-1)}\)のような関数は、ローラン展開を考えるのにふさわしいです。\(z=0,1\)を除外すれば、それは正則な関数となっています。そのような関数が正則でなくなる点は、特異点(singular point)と呼ばれます。
特にローラン展開に関連して役立つ概念が、孤立特異点です。\(z=z_0\)が\(f\)の孤立特異点(isolated singularity)であるとは、\(0<|z-z_0|<R\)において\(f\)が正則であるような半径\(R\)が存在することです。
例えば、\(f(z)=\frac{1}{z(z-1)}\)について、\(z=0,1\)は孤立特異点です。半径としては例えば\(\frac{1}{2}\)を選べば良いですね。\(0<|z|<2\)という領域の選び方をすると、\(z=1\)という特異点が含まれてしまうためローラン展開することはできません。半径を適切に小さく選べば、ローラン展開できるような特異点が孤立特異点です。より一般に、\(\frac{1}{P(z)}\)、\(P\)は多項式という有理関数において、分母の零点は孤立特異点です。
別の例として、対数関数の主値\(f(z)= \mathrm{Log \,}z\)において、\(z=0\)は特異点であり、さらに孤立特異点ではありません。\(z=0\)だけでなく負の実部で正則ではないので、\(z=0\)を中心とする小さい円環領域を考えても、必ず特異点を含んでしまいます。これは非孤立特異点と呼ばれるものです。ローラン展開の議論では孤立特異点のみを持つケースを考えるため、そうでないケースはありますが後回しとしましょう。
ローラン展開の求め方、孤立特異点の分類
ローラン展開の考え方、展開可能であることを知ったところで、具体的にそれを求めてみましょう。
\(f(z)=\frac{1}{z(z-1)}\)を\(z=0\)を中心としてローラン展開してみましょう。
有理関数の展開においては、まず部分分数分解するのが基本です。\(f(z)=-\frac{1}{z} +\frac{1}{z-1}\)となります。
分数の形の展開には、等比級数(幾何級数)の公式
\[ \begin{aligned}\frac{1}{1-w}= \sum_{n=0}^\infty w^n\end{aligned} \]
\(|w|<1\)が使えます。したがって、\(|z|<1\)として、
\[ \begin{aligned}f(z)=-\frac{1}{z}-\frac{1}{1-z} \\ = -\frac{1}{z}-\sum_{n=0}^\infty z^n\end{aligned} \]
と展開することができました。各項が\(z\)のべき乗の形になっているので、これがローラン展開です。
主要部
関数をローラン展開したときに、登場する負のべき乗の項によって、孤立特異点はいくつかに分類されます。負のべき乗の項
\[ \begin{aligned} \frac{a_{-1}}{z-z_0}+ \frac{a_{-2}}{(z-z_0)^2}+\cdots \\ = \sum_{n=1}^\infty \frac{a_{-n}}{(z-z_0)^n}\end{aligned} \]
は、ローラン展開の主要部(principal part)と呼ばれます。
極
さきほどの例
\[ \begin{aligned}f(z)= -\frac{1}{z}-\sum_{n=0}^\infty z^n\end{aligned} \]
において、主要部は\(-\frac{1}{z}\)です。
主要部が0でなく、かつ有限項の場合の孤立特異点は、極(pole)と呼ばれます。上の例ならば、孤立特異点\(z=0\)は極です。その負のべき乗の最大次数を位数(order)と呼びます。\(z=0\)は位数1の極(1位の極とも)です。
極と呼ばれるのは、例えば\(|\frac{1}{z}|\)をグラフにすれば、\(z=0\)において細長い棒(ポール)のようになるからでしょう。
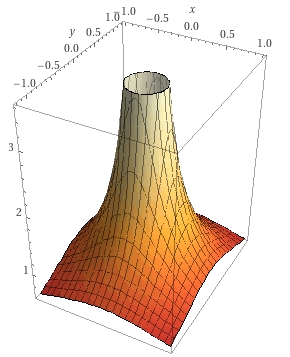
画像引用:1/(x^2+y^2)^(1/2) – WolframAlpha
除去可能特異点
別の例として、\(f(z)=\frac{\sin z}{z}\)を考えましょう。\(\sin z\)は複素数全体で正則なので、\(z=0\)は孤立特異点です。
初等関数を含む関数のローラン展開には、テイラー展開を使うと良いでしょう。
\[ \begin{aligned}\sin z = \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!}z^{2n+1}\end{aligned} \]
なので、
\[ \begin{aligned}\frac{\sin z}{z} = \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!}z^{2n}\end{aligned} \]
です。これがローラン展開です。
負のべき乗は含まず、主要部は0です。このケースでは、ローラン展開は単にテイラー展開となっています。このような特異点\(z=0\)は、除去可能特異点(removable singularity)、可除特異点と呼ばれます。
実際、\(f(0)=1\)と定義することで\(f(z)=\frac{\sin z}{z}\)は正則関数となります。一般に、除去可能特異点があっても、そこを含めて正則に拡張できることが知られています(リーマンの除去可能特異点定理)。
真性特異点
\(f(z)=e^{\frac{1}{z}}\)において、\(z=0\)は孤立特異点です。ローラン展開を求めてみましょう。
\(e^z\)のテイラー展開は
\[ \begin{aligned}e^ z = \sum_{n=0}^\infty \frac{1}{n!}z^{n}\end{aligned} \]
なので、置き換えれば
\[ \begin{aligned}e^ \frac{1}{z} = \sum_{n=0}^\infty \frac{1}{n!}z^{-n}\end{aligned} \]
となります。これがローラン展開です。
主要部が無限項あり、このケースの特異点は真性特異点(essential singularity)と呼ばれます。
以上、ローラン展開とは何か、その求め方、孤立特異点の分類(極、除去可能特異点、真性特異点)を紹介してきました。
ローラン展開をなぜ考えるかと言えば、主要部の係数によって積分が計算できる:留数定理への応用がメインです。留数の考え方を理解するにあたって、まずはいろいろな関数のローラン展開ができるようになりましょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Kreyszig, E: Advanced Engineering Mathematics
Wiley John + Sons (2011-05-03T00:00:01Z)
¥10,314 (中古品)
岩波書店 (2003-12-12T00:00:01Z)
¥2,640
日本評論社 (2009-06-01T00:00:01Z)
¥5,170
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740