逆三角関数arctanのテイラー展開の簡単な求め方

どうも、木村（@kimu3_slime）です。

今回は、逆三角関数\(\mathrm{arctan}\)のテイラー展開の求め方を紹介します。

\(f(z) = \mathrm{arctan\,} z\)をタンジェントの逆関数、アークタンジェントとしましょう。そのテイラー展開（マクローリン展開）は

\[ \begin{aligned}\mathrm{arctan \,}z = z-\frac{z^3}{3}+\frac{z^5}{5}-\cdots \\ \sum_{n=0}^\infty \frac{(-1)^n}{2n+1}z^{2n+1}\end{aligned} \]

と表されます。収束する範囲は\(|z|<1\)です。

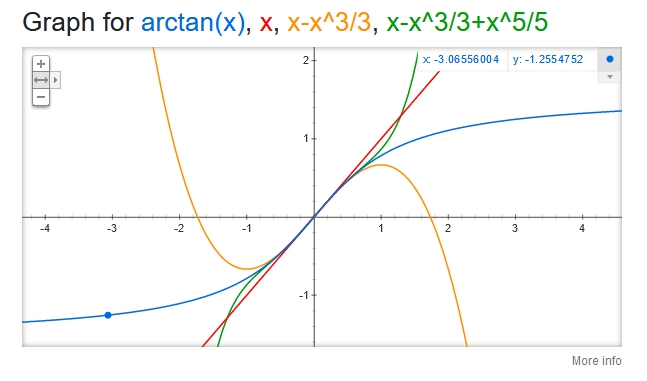
変数を複素数として議論していますが、実変数\(x\)と考えても、全く同じ式が成り立ちます。

（複素のアークタンジェント\( w=\mathrm{arctan\,} z\)は、\(w=a+ib\)と実部虚部を表す時、\(|a|<\frac{\pi}{2}\)と主値を選ぶことで逆関数を作っています。）

さて、アークタンジェントの微分は、

\[ \begin{aligned}(\mathrm{arctan \,}z )^{\prime}= \frac{1}{1+z^2}\end{aligned} \]

となります。これを繰り返し微分して、テイラー級数の係数\(a_n = \frac{f^{(n)}(0)}{n!}\)を計算することは、原理的にできますが大変です。そこで、少し工夫をしましょう。

一般に、等比級数（幾何級数）の公式から、

\[ \begin{aligned}\frac{1}{1-w}= \sum_{n=0}^\infty w^n\end{aligned} \]

\(|w|<1\)が成り立ちます。ここで\(w=-z^2\)と置き換えると、微分の式が級数展開できます。

\[ \begin{aligned} & (\mathrm{arctan \,}z )^{\prime}\\&= \frac{1}{1+z^2}\\&= \sum_{n=0}^\infty (-z^2)^n \\ &= \sum_{n=0}^\infty (-1)^n z^{2n} \end{aligned} \]

ただし、\(|z^2|<1\)、すなわち\(|z|<1\)です。

複素べき級数では、項別に積分できることが知られています。そこで両辺を\(z\)について積分すると、

\[ \begin{aligned} & \mathrm{arctan \,}z \\ &= \int _0 ^z (\sum_{n=0}^\infty (-1)^n w^{2n} )dw \\ &= \sum_{n=0}^\infty (\int _0 ^z (-1)^n w^{2n} dw) \\ &= \sum_{n=0}^\infty (-1)^n [\frac{1}{2n+1}w^{2n+1}]_0^z \\&= \sum_{n=0}^\infty \frac{(-1)^n}{2n+1}z^{2n+1}\end{aligned} \]

と求められました。逆関数の定義から、\(\mathrm{arctan \,}0=0\)であることに注意しましょう。項別積分（や微分）では収束半径は変わらず、\(|z|<1\)において級数は収束します。

（厳密に言えば、\(\int_0 ^z dw\)は、\(0,z\)をつなぐ直線の経路\(c\)における複素線積分を表しています。）

以上、逆三角関数arctanのテイラー級数展開の求め方を紹介してきました。

arcsinやarccosのテイラー級数は少し複雑になりますが、それに比べてarctanのテイラー展開は簡単です。

arctanの微分を幾何級数として展開することで、元の関数の級数展開が求められるのは便利です。形式的に導けるので、ぜひ利用してみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。