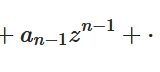べき級数の収束発散が円盤によって分かれること：収束半径の性質

どうも、木村（@kimu3_slime）です。

今回は、べき級数の収束発散が円盤によって分かれること、収束半径の性質を紹介します。

\(z_0\)を中心とする複素べき級数

\[ \begin{aligned}f(z )= \sum _{k=0} ^ \infty a_k (z-z_0)^k\end{aligned} \]

の収束、発散について考えましょう。

べき級数が\(|z-z_0|<r\)で絶対収束し、\(|z-z_0|>r\)で発散するとき、その\(r>0\)をべき級数の収束半径と呼ぶのでした。

参考：べき級数の収束半径とは何か、テイラー展開を例にした求め方、複素べき級数、収束半径とは：指数・三角関数を例に

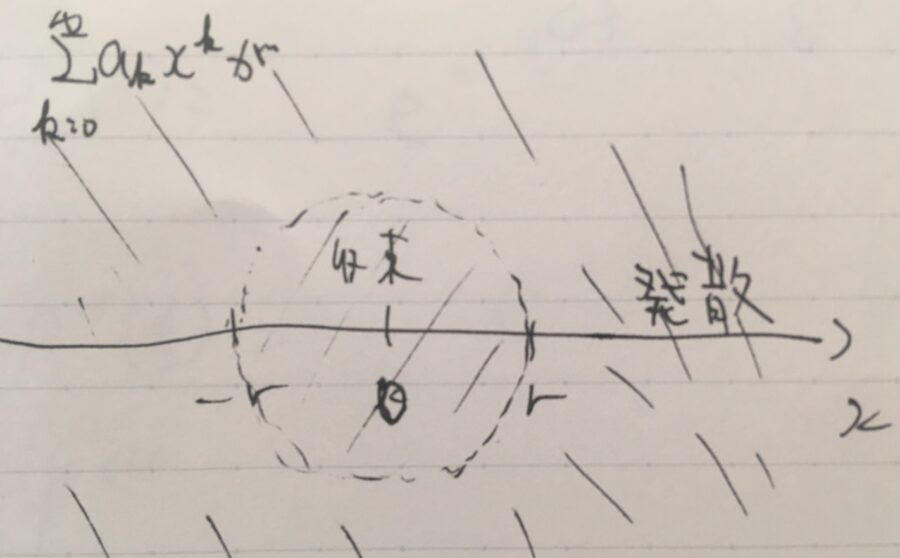
このように収束半径は定義されるわけですが、本当にべき級数は必ず円盤によって収束・発散が分かれるのでしょうか。何か例外はないのでしょうか。

実際は、どんなべき級数も、円盤によって収束発散が分かれます。それを示すのが次の結果です。

\[ \begin{aligned}f(z )= \sum _{k=0} ^ \infty a_k (z-z_0)^k\end{aligned} \]について考える。

べき級数が\(z=z_1\)（\(z_1 \neq z_0\)）で収束すると仮定する。このとき、\(z_1\)より\(z_0\)に近いすべての\(z\)について（\(|z-z_0|< |z_1 -z_0|\)）、級数は絶対収束する。
べき級数が\(z=z_2\)（\(z_2 \neq z_0\)）で発散すると仮定する。このとき、\(z_1\)より\(z_0\)から遠いすべての\(z\)について（\(|z-z_0|> |z_2 -z_0|\)）、級数は発散する。

この結果を証明しましょう。方針としては、他の級数と比較することです。

まず、級数が\(z=z_1\)で収束しているケースを考えます。\(z\)を\(|z-z_0|< |z_1 -z_0|\)として、べき級数が収束することを示しましょう。

べき級数の各項を、収束しているケース\(z_1-z_0\)によって上から評価しましょう。

\[ \begin{aligned} & |a_k(z-z_0)^k| \\&= |a_k (z_1-z_0)^k(\frac{z-z_0}{z_1-z_0})^k|\end{aligned} \]

と変形できます。ここで\(\sum a_k(z_1-z_0)^k\)が収束していることから、各項は\(k\to \infty\)で0に収束します。収束する数列は有界なので（収束の定義から）、

\[ \begin{aligned} |a_k (z_1-z_0)^k| < M\end{aligned} \]

を満たす定数\(M\)が存在します。したがって、さきほどの式に戻せば

\[ \begin{aligned} & |a_k(z-z_0)^k|\\ &= |a_k (z_1-z_0)^k(\frac{z-z_0}{z_1-z_0})^k|\\&<&M|\frac{z-z_0}{z_1-z_0}|^k\end{aligned} \]

が成り立ちます。両辺で級数を取ると、

\[ \begin{aligned}\sum _{k=0}^\infty |a_k(z-z_0)^k| \leq M\sum _{k=0}^\infty |\frac{z-z_0}{z_1-z_0}|^k \end{aligned} \]

です。ここで仮定\(|z-z_0|< |z_1 -z_0|\)より、\(|\frac{z-z_0}{z_1-z_0}|<1\)なので、右辺は等比級数（幾何級数）の性質により収束します。

よって、比較によって左辺も収束すること、べき級数が\(z\)において絶対収束することがわかりました。

続いて、級数が\(z=z_2\)で発散しているケースを考えましょう。\(|z-z_0|> |z_2 -z_0|\)を満たす\(z\)について、べき級数が発散することを示します。

背理法として、\(|z-z_0|> |z_2 -z_0|\)を満たす\(z\)で、べき級数が収束するものがあったとしましょう。このとき、さきほどの主張から、\(z_2\)ではべき級数が収束することが導かれます。これは仮定に矛盾します。よって、もともとの主張、\(z\)ではべき級数が発散することが示せました。

まとめましょう。

1つでも収束する点\(z_1\)が見つかると、そこでの距離\(r=|z_1-z_0|\)を基準として中心に近いならばすべて収束します。逆に、1つでも収束しない点\(z_2\)があれば、中心から遠い点ではすべて発散します。\(z_1,z_2\)での級数が門番のように、円内や円外の点を押さえつけて評価できるわけです。

今回の議論は、円盤の内外で収束発散が分かれることを述べたのみで、円周上\(|z-z_0|=r\)では何も言ってないことに注意しましょう。\(z_1\)で収束するからと言って、同じ円周上の点では、収束することも発散することもあります（例えば、\(\log (1+x)\)の級数展開は、\(x=1\)で収束するが、\(x=-1\)で発散する）。円周上での収束発散は、個別の級数にもとづき議論する必要があります。

以上、べき級数の収束発散が円盤によって分かれること、収束半径の性質について紹介してきました。

今回の議論から、収束半径を簡単に見つけられるケースも増えます。例えば、\(\frac{1}{z}\)の\(z=1\)を中心にしたべき級数展開を考えましょう。小さな円盤を考えて広げていくと、\(z=0\)と発散する点にぶつかります。そこに達するまで\(|z-1|<1\)では収束していました。したがって、収束半径は\(r=1\)と議論ができるわけです。

レシオテストやルートテストで定量的に収束半径を求めるのも良いですが、収束半径の定義にもとづいた定性的な議論をするために、今回の話を知っておくと良いでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。