どうも、木村(@kimu3_slime)です。
今回は、絶対サイン波とは何か、そのフーリエ級数展開の求め方を紹介します。
絶対サイン波
絶対サイン波(absolute sine wave)とは、サイン波の正の部分が繰り返す波のことです。
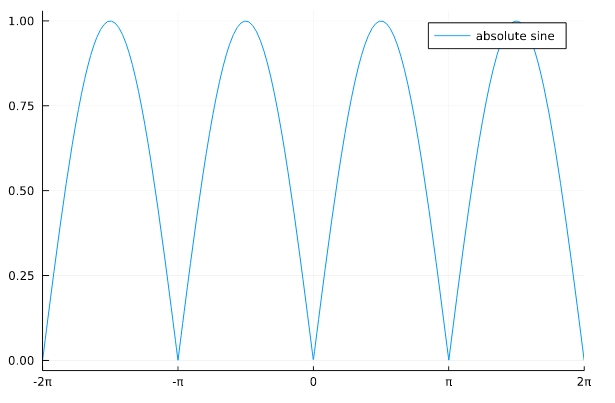
数学的には、サインの絶対値を取った関数
\[ \begin{aligned}f(x) = |\sin x|\end{aligned} \]
のことです。これは通常のサイン
\[ \begin{aligned}f(x)=\sin x \quad (0 \leq x \leq \pi)\end{aligned} \]
を偶関数(\(f(x)=f(-x)\))として周期的に拡張した関数とも言えます。
この波形の音は、セミサイン波(semisine wave)とも呼ばれています。聞いてみると、サイン波よりはにごりがありますが、のこぎり波ほどではありません。
フーリエ級数展開の求め方
絶対サイン波のフーリエ級数展開を求めてみましょう。
今回の設定では、それは偶関数なので、偶関数のフーリエ級数展開として次のように単純化されます。\(f\)は周期\(2\pi\)の関数として捉えています。
\[ \begin{aligned}f(x)= a_0 +\sum_{k=1}^\infty a_n \cos nx\end{aligned} \]
\[ \begin{aligned}a_0 =\frac{1}{\pi}\int_0^\pi f(x)dx\end{aligned} \]
\[ \begin{aligned}a_n = \frac{2}{\pi}\int_0^\pi f(x) \cos nx dx \end{aligned} \]
では、これらを計算してみます。積分範囲\(0 \leq x \leq \pi\)においては、サインは正なので、\(f(x)= \sin x\)そのものであることに注意しましょう。
まず、
\[ \begin{aligned} a_0 &=\frac{1}{\pi}\int_0^\pi \sin x dx \\ &= \frac{1}{\pi}[-\cos x]_0 ^{\pi}\\ &= \frac{2}{\pi} \end{aligned} \]
です。そして、三角関数の加法定理、積和の公式
\[ \begin{aligned}\sin \alpha \cos \beta \\= \frac{1}{2}(\sin (\alpha +\beta)+\sin (\alpha -\beta))\end{aligned} \]
から、
\[ \begin{aligned} &a_n \\&= \frac{2}{\pi}\int_0^\pi \sin x \cos nx dx \\ &= \frac{1}{\pi}\int_0^\pi (\sin (n+1)x + \sin (1-n)x) dx\\ &= \frac{1}{\pi}([-\frac{1}{n+1} \cos (n+1)x +\frac{1}{n-1}\cos (n-1)x]_0^{\pi})\\ &= \frac{1}{\pi}(-\frac{1}{n+1}\cos (n+1)\pi +\frac{1}{n-1} \cos (n-1)\pi \\ &+\frac{1}{n+1} – \frac{1}{n-1})\\ &=\frac{2}{ (n+1)(n-1) \pi}(\cos (n-1)\pi -1) \\ &= \begin{cases}-\frac{4}{ (n^2-1)\pi} & (nが偶数 )\\0 & (nが奇数)\end{cases}\end{aligned} \]
となりました。\(\cos (n+1)\pi = \cos (n-1)\pi\)であることに注意、角度の差が\(2\pi\)なのでコサインは等しいです。
フーリエ係数、すなわち各周波数にける\(\cos nx\)の振幅、スペクトルを図示すると次の通りです。
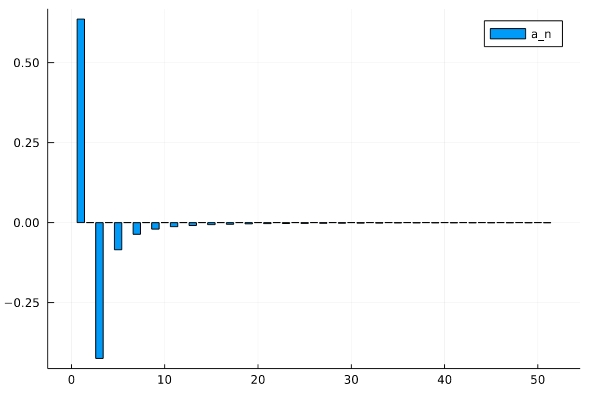
偶数番のみの成分が含まれていること、一番最初\(a_0\)のみが正で、以降が負であることがわかりますね。
絶対サイン波のフーリエ級数展開は、次のようになりました。偶数番を\(n=2k\)と表しています。
\[ \begin{aligned}f(x)=\frac{2}{\pi} – \sum_{k=1}^\infty \frac{4}{(4k^2-1)\pi} \cos 2k x \\ =\frac{2}{\pi}-\frac{4}{3\pi}\cos 2x – \frac{4}{15\pi} \cos 4x -\cdots\end{aligned} \]
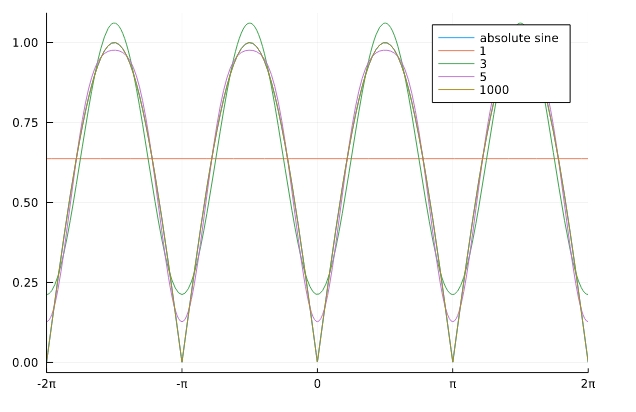
結果として、絶対サイン波は定数とコサインの重ね合わせで表現できます。サインでなくコサインなのは意外に思えますが、波の真ん中付近の直線\(\frac{2}{\pi}\)とマイナスコサイン\(-\cos \)の足し合わせとするなら納得です。
以上、絶対サイン波とは何か、そのフーリエ級数展開の求め方を紹介してきました。
矩形波、のこぎり波、三角波についで単純な結果なので、ぜひ自分でも計算してみてはいかがでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
Partial Differential Equations (Graduate Studies in Mathematics)
Amer Mathematical Society (2010-04-02T00:00:01Z)
¥9,531 (中古品)
こちらもおすすめ
矩形波とは:フーリエ級数展開の求め方、ギブス現象、ライプニッツの級数