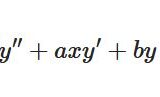球面におけるラプラス方程式の解き方：変数分離法

どうも、木村（@kimu3_slime）です。

今回は、球面におけるラプラス方程式の解き方として、変数分離法を紹介します。

3次元空間におけるラプラス方程式は、

\[ \begin{aligned}\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}+\frac{\partial^2 u}{\partial z^2}=0\end{aligned} \]

です。2回偏微分の和（ラプラシアン）を球面座標（3次元極座標）

\[ \begin{aligned}x=r\cos \theta \sin \phi \\y = r\sin \theta \sin \phi \\ z= r\cos \phi\end{aligned} \]

を使って表すと（\(\theta\)が\(x,y\)平面における角度であることに注意）、

\[ \begin{aligned}\frac{1}{r^2}(\frac{\partial}{\partial r}(r^2 \frac{\partial u}{\partial r}) +\frac{1}{\sin \phi}\frac{\partial}{\partial \phi} (\sin \phi \frac{\partial u}{\partial \phi}))=0\end{aligned} \]

となることが知られています。ここでは、半径\(R\)の球を考え、

\[ \begin{aligned}u(R,\phi)=f(\phi)\end{aligned} \]

\[ \begin{aligned}\lim_{r\to \infty}u(r,\phi)=0\end{aligned} \]

という境界条件を考えましょう。球対称な境界条件を考えているので、解は\(\theta\)に依存しないものと仮定しています。

では、球面におけるラプラス方程式

を変数分離法によって解いていきましょう。

\(u(r,\phi)=G(r)H(\phi)\)と変数分離される解を考えます。\(r^2\)をかけて、方程式に代入すれば

\[ \begin{aligned}\frac{d}{d r}(r^2 \frac{d G}{d r} H(\phi)) =-\frac{1}{\sin \phi}\frac{d}{d \phi} (\sin \phi \frac{d H}{d \phi}G(r))\end{aligned} \]

です。\(u\)として0でない解（非自明解）を考えているので、両辺を\(GH \neq 0\)で割れば、

\[ \begin{aligned}\frac{1}{G}\frac{d}{d r}(r^2 \frac{d G}{d r} ) =-\frac{1}{H\sin \phi}\frac{d}{d \phi} (\sin \phi \frac{d H}{d \phi})\end{aligned} \]

となります。左辺は\(r\)のみの関数、右辺は\(\phi\)のみの関数なので、両辺は定数でなければなりません。その定数（分離定数）を\(\lambda\)と置くと、

\[ \begin{aligned}\frac{d}{d r}(r^2 \frac{d G}{d r} ) =\lambda G\end{aligned} \]

\[ \begin{aligned}\frac{1}{\sin \phi}\frac{d}{d \phi} (\sin \phi \frac{d H}{d \phi})+\lambda H=0\end{aligned} \]

という2つの常微分方程式が得られました。

まず、前者は

\[ \begin{aligned}r^2 G^{\prime \prime}+2rG^{\prime}-\lambda G=0\end{aligned} \]

と表せます。これはオイラー・コーシーの微分方程式です。この方程式が簡単な形で解けて、後の都合も良くなるように、\(\lambda = n(n+1)\)のときを考えましょう。すると、解として

\[ \begin{aligned}G_{1n}(r)=r^n\end{aligned} \]

\[ \begin{aligned}G_{2n}(r)=\frac{1}{r^{n+1}}\end{aligned} \]

が得られます。

もう一方の方程式

\[ \begin{aligned}\frac{1}{\sin \phi}\frac{d}{d \phi} (\sin \phi \frac{d H}{d \phi})+\lambda H=0\end{aligned} \]

を解くために、\(w= \cos \phi\)と変数変換します。すると、合成関数の微分から、

\[ \begin{aligned} & \frac{1}{\sin \phi}\frac{d}{d w} (\sin \phi \frac{dH}{dw}\frac{dw}{d\phi}) \frac{dw}{d\phi}+\lambda H \\&= \frac{-\sin \phi}{\sin \phi} \frac{d}{d w} (-(\sin \phi)^2 \frac{dH}{dw})+\lambda H\\&=\frac{d}{d w} ((1-(\cos \phi)^2) \frac{dH}{dw})+\lambda H \\ &= \frac{d}{d w} ((1-w^2 )\frac{dH}{dw})+\lambda H \\&=0 \end{aligned} \]

です。これはルジャンドルの微分方程式として知られ、その解はルジャンドル多項式\(P_n\)となります。

\[ \begin{aligned}H_n =P_n (w)= P_n(\cos \phi)\end{aligned} \]

よって、ラプラス方程式の解としては

\[ \begin{aligned}u_{1n}=A_n r^n P_n(\cos \phi)\end{aligned} \]

\[ \begin{aligned}u_{2n}=B_n \frac{1}{r^{n+1}} P_n(\cos \phi)\end{aligned} \]

が得られました。

これらの解を重ね合わせることで、境界条件を満たす解が構成できます。ですが、長くなるので別の記事にしようと思います。

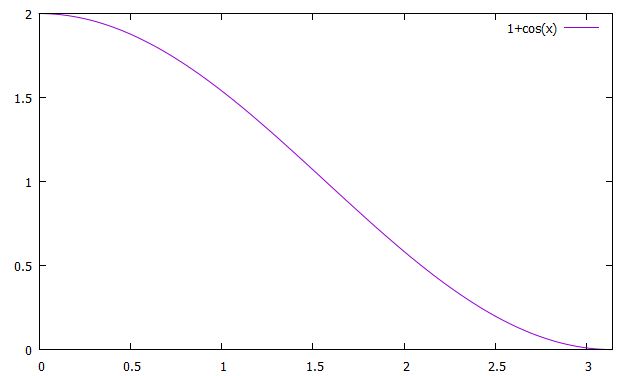
例えば、\(A_n =1\)、\(r=1\)のとき、\(u_{1,0}+u_{1,1}=1+\cos \phi\)のグラフは次のようになります。