どうも、木村(@kimu3_slime)です。
今回は、1次元のポアソン方程式の解き方を紹介します。
考える方程式は、
\[ \begin{aligned}-\frac{d^2 u}{d x^2} =f(x)\end{aligned} \]
です。多次元だと左辺は2回偏微分の和となりますが、1次元なので単なる2回微分となっています。形としては、非同次(非斉次)の2階線形常微分方程式です。
非同次の方程式の解き方としては、未定係数法、定数変化法、ラプラス変換などが知られています。
今回は、定数変化法によって一般的な解を得てみましょう。
同次形の方程式
\[ \begin{aligned}-\frac{d^2 u}{d x^2} =0\end{aligned} \]
の解は、\(u(x)=C_1 x+ C_2\)です。
そこで、\(u_0(x)=C_1(x) x+C_2(x)\)と係数を関数に置き換えたものと仮定します。その微分は、
\[ \begin{aligned}u_0^{\prime} = C_1^{\prime} x +C_1 +C_2^{\prime}\end{aligned} \]
です。特殊解を得るために、\(C_1^{\prime} x +C_2^{\prime} =0\)という仮定を足しましょう。すると、\(u_0^{\prime \prime}= C_1 ^{\prime}\)です。これをポアソン方程式に代入しましょう。すると、
\[ \begin{aligned}-C_1^{\prime}=f(x)\end{aligned} \]
です。一方、仮定から
\[ \begin{aligned} C_2^{\prime}&= -C_1^{\prime}x \\ &= xf(x)\ \end{aligned} \]
となります。それぞれを積分することで、係数を決定でき、
\[ \begin{aligned}u(x)= -x(\int_{x_0}^x f(s)ds+C_3) + \int_{x_0}^x sf(s)ds +C_4 \end{aligned} \]
がポアソン方程式の解であるとわかりました。
具体的にひとつ解を得てみましょう。
考える区間を\([0,\pi]\)、非同次項を\(f(x)=\sin x\)とします。境界条件を\(u(0)=0,u(\pi) =1\)としましょう。積分を計算すれば、
\[ \begin{aligned}\int_0 ^x \sin s ds=1-\cos x\end{aligned} \]
\[ \begin{aligned}\int _0 ^x s \sin s ds =\sin x -x \cos x\end{aligned} \]
なので、
\[ \begin{aligned}u(x)=-x(1-\cos x+C_3)\\ +\sin x -x \cos x +C_4\\ = -x(1+C_3)+\sin x +C_4\end{aligned} \]
となります。境界条件より、\(C_4 =0\)、\(C_3 = -1-\frac{1}{\pi}\)です。よって、解は
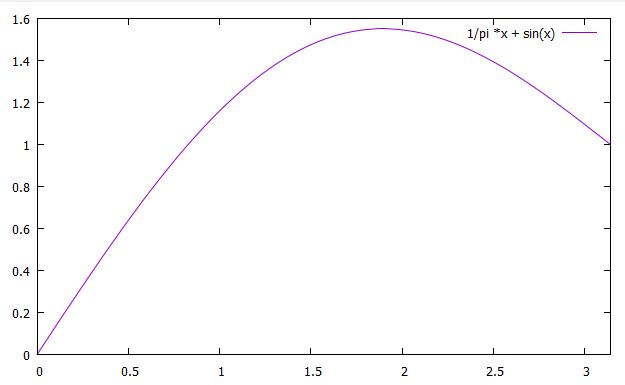
\[ \begin{aligned}u(x)=\frac{1}{\pi}x +\sin x\end{aligned} \]
とわかりました。
以上、1次元のポアソン方程式を、定数変化法を使って解く方法を紹介してきました。
2次元以上のポアソン方程式の境界値問題や全空間における問題は、グリーン関数や基本解という考えを用います。
まずは簡単なケースとして、1次元のポアソン方程式を解いてみると、イメージがつかみやすいのではないでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
Partial Differential Equations (Graduate Studies in Mathematics)
Amer Mathematical Society (2010-04-02T00:00:01Z)
¥9,531 (中古品)