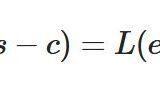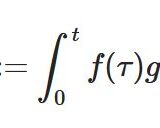どうも、木村(@kimu3_slime)です。
今回は、デルタ関数とは何か、そのラプラス変換、微分方程式への応用を紹介します。
デルタ関数、超関数とは
デルタ関数は、瞬間的な外力、衝撃力(impulsive force)を表すために使われる「関数」です。
それは次のように説明されます。
\[ \begin{aligned}\delta (t)= \begin{cases}\infty & (t=0 )\\ 0& (t \neq 0)\end{cases}\end{aligned} \]
\[ \begin{aligned}\int_0 ^\infty \delta (t)dt =1\end{aligned} \]
つまり、\(t=0\)という一瞬だけ値を持ち、積分(力積)が一定のものです。これはディラックのデルタ関数(Dirac delta function)と呼ばれます。
例えば、
\[ \begin{aligned}f_d(t)= \begin{cases}\frac{1}{d} & (0 \leq t \leq d)\\0 & (それ以外)\end{cases}\end{aligned} \]
という関数を考えましょう。その積分は\(d\)によらず、常に一定です\( \int_0 ^\infty f_d(t)dt=1\)。そして、\(d\to 0\)とすると、その値は限りなく大きくなっていき、デルタ関数に近づいていきますね。デルタ関数は、短い瞬間に大きな変化をもたらす関数を理想化したものと言えます。
(他にも、さまざまな形の関数でのデルタ関数の近似が知られています。例えば正規分布の密度関数の分散を0に近づける極限。)
デルタ関数は関数という名前がついていますが、無限大を値を持つため、通常の関数ではありません(数から数への対応を関数と呼ぶ)。
しかし、シュワルツの超関数(distribution, generalized function)という枠組みでそれを定義することができます。
他のなめらかな関数\(g(t)\)との積の積分を考えましょう。\(G(t)\)をその原始関数として、平均値の定理より
\[ \begin{aligned} \int_0 ^\infty g(t)f_d(t)dt &= \int_0 ^d g(t) \frac{1}{d}dt \\ &=[G(t) \frac{1}{d}]_0^d \\ &= \frac{1}{d}(G(d)-G(0) )\\&= g(c)\end{aligned} \]
となる\(c\)が存在します。\(0 <c<d\)を満たすので、
\[ \begin{aligned} \lim_{d \to 0} \int_0 ^\infty g(t)f_d(t)dt = g(0)\end{aligned} \]
です。この結果に合わせて、デルタ関数は
\[ \begin{aligned}\int_0 ^\infty g(t)\delta(t)dt =g(0)\end{aligned} \]
を満たすものとしましょう。
つまり、デルタ関数とは、インプットとなるなめらかな関数\(g \in D\)(テスト関数)に対し、\(g(0) \in \mathbb{R}\)を返す線形な関数(線形汎関数)の一種で、次のように定義されます。
\[ \begin{aligned}\langle \delta ,g\rangle := g(0)\end{aligned} \]
つまり、\(\delta\)は関数\(g\)を変数とする関数です。\(\delta (g)\)と書かずに、\(\langle \delta ,g\rangle\)と書くのは、積分の内積の記号と合わたもので、
\[ \begin{aligned} \langle \delta ,g\rangle &= \int_0 ^\infty g(t)\delta(t)dt \\ &=g(0) \end{aligned} \]
と解釈することができます。
(最初に述べたラフな定義\(\delta (0)=\infty\)だと、通常の関数として考えたら、1点\(t=0\)以外での値が0なので、積分値は0となってしまいます。超関数の枠組みなら、そもそも他の関数との積分によって定義されるので、期待した式が正当化されるわけです。)
(単位ステップ関数・ヘビサイド関数の「微分」は、デルタ関数であることが知られています。)
デルタ関数のラプラス変換
超関数に対しても、通常の関数と同じように、ラプラス変換を定義することができます。
デルタ関数のラプラス変換ならば、
\[ \begin{aligned}L(\delta)(s):= \langle \delta, e^{-st}\rangle\end{aligned} \]
といったように。
これを計算して求めてみましょう。さきほどの定義(性質)に従えば、
\[ \begin{aligned} \langle \delta, e^{-st}\rangle &= \int_0 ^\infty e^{-st}\delta(t)dt \\ &= e^{0}\\&= 1\end{aligned} \]
です。
平行移動(シフト)\(\delta (t-a)\)に対応して、中心\(a\)でのデルタ関数\(\delta_a\)を\(\langle \delta _a , g\rangle:=g(a)\)と定義します。すると、そのラプラス変換は
\[ \begin{aligned}L(\delta _a) (s)= e^{-as}\end{aligned} \]
となりますね。
微分方程式への応用
デルタ関数、そのラプラス変換を微分方程式へ応用しましょう。おもりバネダンパ系の運動方程式として、
\[ \begin{aligned}\frac{d^2 x}{dt^2} +2\frac{dx}{dt} +x =\delta(t)\end{aligned} \]
を考えましょう。右辺に外力、特に衝撃力として\(\delta (t)\)が加わっています。
これをラプラス変換によって解いていきます。
\[ \begin{aligned}L(\frac{dx}{dt})= sL(f)-x(0)\end{aligned} \]
\[ \begin{aligned}L(\frac{d^2x}{dt^2})= s^2L(x)-sx(0)-\frac{dx}{dt}(0)\end{aligned} \]
で、特におもりを原点から静かに離すケース、\(x(0)=\frac{dx}{dt}=0\)を考えましょう。すると、
\[ \begin{aligned}(s^2+2s +1)L(x)= 1\end{aligned} \]
です(デルタ関数のラプラス変換は1)。したがって、
\[ \begin{aligned} L(x)&= \frac{1}{(s+1)^2} \end{aligned} \]
となります。一般に、
\[ \begin{aligned}L(te^{bt}) = \frac{1}{(s-b)^2}\end{aligned} \]
となるので(部分積分と第一シフト定理)、\(b=-1\)として方程式を逆ラプラス変換すれば
\[ \begin{aligned}x(t) = te^{-t}\end{aligned} \]
と解が得られました。
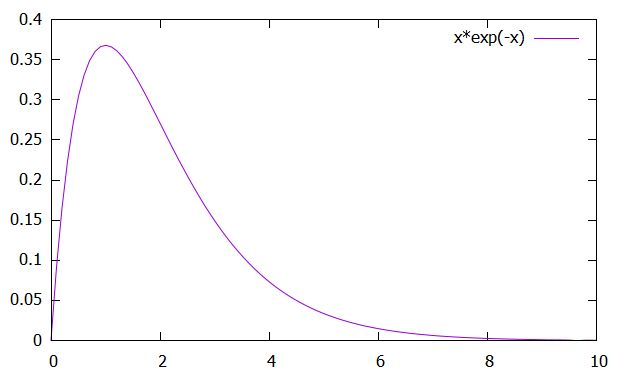
減衰係数、バネ定数のバランスから、方程式は臨界減衰のケースに対応しています。外力がなければ、初期位置・速度が0のときは、おもりは原点に留まり続けます。
しかし今回は、初期位置・速度が0であったにもかかわらず、\(t=0\)での瞬間的な外力によっておもりの位置は変化しているのがわかりますね。
以上、デルタ関数とは何か、ラプラス変換、微分方程式への応用を紹介してきました。
超関数の話は少しわかりにくかったかもしれませんが、衝撃力の表現としてデルタ関数が使えるのを感じてもらえたと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
De Gruyter (2013-03-15T00:00:01Z)
¥3,319
こちらもおすすめ
無限集合の濃度とは? 写像の全単射、可算無限、カントールの対角線論法
ラプラス変換の第一シフト定理(s推移法則)とは、証明、応用例
おもりバネダンパ系:減衰振動の運動方程式、微分方程式の解き方