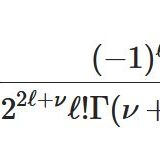どうも、木村(@kimu3_slime)です。
今回は、微分方程式を解法であるフロベニウスの方法とは何か、ベッセル方程式、第一種ベッセル関数を例に紹介します。
フロベニウスの方法とは
ベッセル方程式(Bessel’s equation)とは、
\[ \begin{aligned}x^2 y^{\prime \prime}+xy^{\prime} +(x^2-\nu ^2)y =0\end{aligned} \]
と表される微分方程式です。\(\nu \geq 0\)は実数のパラメータです。この方程式は、例えば円筒座標系におけるラプラス方程式の解を得る中で表れます。
この方程式は、そのままのべき級数解法によって解くことができません。
\[ \begin{aligned} y^{\prime \prime}+b(x)y^{\prime} +c(x)y =0\end{aligned} \]
と表すとき、\(b,c\)が\(x=0\)で解析的(べき級数展開可能)ならば、べき級数展開によって解を得ることができます。解ける例としてはルジャンドルの方程式がああります。
しかし、ベッセル方程式の場合は、
\[ \begin{aligned} y^{\prime \prime}+\frac{1}{x}y^{\prime} +(1- \frac{\nu^2}{x^2})y =0\end{aligned} \]
のように、係数が\(x=0\)で解析的ではありません。このとき、\(x=0\)を特異点(singular point)と呼びます。
係数が特異点を持つ微分方程式について、べき級数解法を拡張した方法が、フロベニウスの方法(Frobenius Method)です。
\(b(x),c(x)\)を\(x=0\)において解析的とする。
\[ \begin{aligned} y^{\prime \prime}+\frac{b(x)}{x}y^{\prime} +(1- \frac{c(x)}{x^2})y =0\end{aligned} \]
と表される方程式は、
\[ \begin{aligned}y(x)=x^r \sum_{k=0}^\infty a_k x^k\end{aligned} \]
と表される解を少なくともひとつ持つ。
(もうひとつの解は、これと似た形で見つかる。)
ベッセルの方程式は、\(b(x)=1\)、\(c(x)=x^2-\nu^2 \)で、これらは\(x=0\)において解析的なので、フロベニウスの方法が適用できます。
ベッセル方程式の解き方、第一種ベッセル関数とは
今回は、簡単のため\(\nu =n\)、\(n\)は自然数(非負整数)のケースを考えます。
フロベニウスの方法によると、
\[ \begin{aligned}y(x)= \sum_{k=0}^\infty a_k x^{k+r}\end{aligned} \]
の形の解が見つかります。これとその微分を方程式に代入し、次数\(r\)と係数を求めましょう。
すると、
\[ \begin{aligned}\sum_{k=0}^\infty (k+r)(k+r-1)a_k x^{k+r}+\sum_{k=0}^\infty (k+r)a_k x^{k+r}\\ +\sum_{k=0}^\infty a_k x^{k+r+2}-\nu^2 \sum_{k=0}^\infty a_k x^{k+r}=0\end{aligned} \]
が得られます。\(x^r \)の項の係数を比較すると、
\[ \begin{aligned}r(r-1)a_0 +ra_0 -\nu ^2 a_0 =0\end{aligned} \]
です。これが\(a_0\)によらずに成り立つためには、
\[ \begin{aligned}(r+\nu) (r-\nu)=0\end{aligned} \]
である必要があります。指数\(r\)を決定するこの方程式は、決定方程式(indicial equation)と呼ばれるものです。
その解は、\(r_1 =\nu ,r_2 =-\nu\)です。決定方程式の解の様子によって、解の形は変わります。
\(r= \nu \)のときの解を求めましょう。\(x^{r+1}\)次の項、\(x^{r+2}\)次以降の係数を比較すると、
\[ \begin{aligned}(r+1)ra_1+(r+1)a_1 – \nu^2 a_1 =0\end{aligned} \]
\[ \begin{aligned}(k+r)(k+r-1)a_k +(k+r)a_k\\ +a_{k-2}-\nu^2 a_k=0\end{aligned} \]
が得られます。1番目の式に\(r=\nu\)を代入すれば、
\[ \begin{aligned}(2\nu +1) a_1 =0\end{aligned} \]
で、\(\nu \geq 0\)なので\(a_1=0\)です。2番目の式からは、
\[ \begin{aligned} a_k =-\frac{1}{k(2\nu +k)}a_{k-2}\end{aligned} \]
が得られます。\(a_1=0\)なので、奇数次の係数はすべて\(0\)となります。したがって、偶数次\(k=2\ell\)のケースを計算しましょう。
\[ \begin{aligned}a_{2\ell}=-\frac{1}{2^2 \ell (\nu+\ell)}a_{2\ell-2}\end{aligned} \]
となります。試しに計算すると、
\[ \begin{aligned}a_2 = -\frac{1}{2^2 (\nu+1)}a_{0} \end{aligned} \]
\[ \begin{aligned}a_4 =-\frac{1}{2^2 \cdot2 (\nu+2)}a_{2}\\
= -\frac{1}{2^4 \cdot 2! (\nu+1)(\nu+2)}a_{0}\end{aligned} \]
で、一般には
\[ \begin{aligned}a_{2\ell}=\frac{(-1)^\ell }{2^{2\ell} \ell! (\nu+1)\cdots(\nu+\ell)}a_{0}\end{aligned} \]
です。
\(\nu =n\)のとき、係数がシンプルになる\(a_0\)の選び方をします。すなわち、\(a_0 =\frac{1}{2^n n!}\)とします。すると、さきほどの式から
\[ \begin{aligned}a_{2\ell}=\frac{(-1)^\ell }{2^{2\ell} \ell! (n+1)\cdots(n+\ell)}\frac{1}{2^n n!}\\ =\frac{(-1)^\ell }{2^{2\ell+n} \ell! (n+\ell)!}\end{aligned} \]
です。よって、解は
\[ \begin{aligned}J_n(x)= \sum_{\ell=0}^\infty \frac{(-1)^\ell }{2^{2\ell+n} \ell! (n+\ell)!} x^{2\ell +n }\end{aligned} \]
と求められました。この級数はすべての\(x\)について収束します(レシオテスト)。
\(J_n\)は次数\(n\)の第一種ベッセル関数(Bessel function of the first kind)と呼ばれます。
(もう一種の線形独立な解は、第二種ベッセル関数と呼ばれます。\(J_{-n}\)は線形独立でなく、別の形の級数展開をする必要がある。別記事で紹介予定。)

画像引用:bessel function j0 – Wolfram
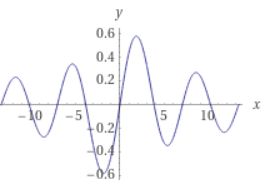
画像引用:bessel function 1 – Wolfram
第一種ベッセル関数は、\(x\)が大きくなると三角関数に漸近していくことが知られています。
また今回は整数\(\nu =n\)のケースを考えましたが、非整数のケースについてはガンマ関数を使って表示することができます。
以上、フロベニウスの方法とは何か、ベッセル方程式を例に紹介し、解として第一種ベッセル関数を得ました。
係数に特異性がある場合でも、級数展開の形を少し変えることで、無事に解くことができましたね。級数解法は便利なのがわかります。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)