高階常微分方程式の連立形への書き換えについて

どうも、木村（@kimu3_slime）です。

今回は、高階常微分方程式の連立形への書き換えについて紹介します。\[ \begin{aligned} \frac{dx_1}{dt}&= x_2 \\ \frac{dx_2}{dt}&= -\frac{k}{m}x_1\end{aligned} \]

微分方程式の解の定性的な理論、力学系理論では、しばしば連立形の常微分方程式（system of ODEs）を考えます。多くの単独の高階常微分方程式は、連立形に書き換えることができます。

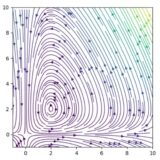
例えば、おもりバネの運動の微分方程式は

\[ \begin{aligned}m\frac{d^2x}{dt^2}= -kx\end{aligned} \]

と表されます。これを連立形に書き換えるために、\(x_1=x,x_2 = \frac{dx}{dt}\)と新たな変数を導入しましょう。すると、それぞれの式を微分すれば

\[ \begin{aligned} \frac{dx_1}{dt}&= x_2 \\ \frac{dx_2}{dt}&= -\frac{k}{m}x_1\end{aligned} \]

と表されます。これは連立線形常微分方程式ですね。

\[ \begin{aligned} \begin{pmatrix} \frac{dx_1}{dt}\\ \frac{dx_2}{dt} \end{pmatrix} =\begin{pmatrix} 0 &1\\ -\frac{k}{m}&0 \end{pmatrix} \begin{pmatrix}x_1\\x_2 \end{pmatrix}\end{aligned} \]

と行列を使って表せます。

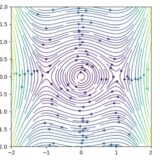
別の例として、減衰振り子の微分方程式は

\[ \begin{aligned}m\frac{d^2 x}{dt^2} = -k \sin x -c\frac{dx}{dt}\end{aligned} \]

と表されます。これも同様に書き換えられます。\(x_1=x,x_2 = \frac{dx}{dt}\)と置くと、その微分をまとめれば

\[ \begin{aligned} \frac{dx_1}{dt}&= x_2 \\ \frac{dx_2}{dt}&= -\frac{k}{m} \sin x_1-\frac{c}{m}x_2\end{aligned} \]

となりますね。この方程式は非線形で、行列を使っては表せません。

一般的な高階微分方程式、\(N\)階の常微分方程式を考えましょう。

\[ \begin{aligned}\frac{d^N x}{dt ^N} =F(x,\frac{dx}{dt},\dots,\frac{dx^{N-1}}{dt^{N-1}},t)\end{aligned} \]

と表される形を考えます。最高階の微分が取り出された方程式は、陽に表された（explicit）常微分方程式、正規形の微分方程式と呼ばれるものです。

この方程式は、\(x_1=x,x_2=\frac{dx}{dt},\dots,x_N =\frac{dx^{N-1}}{dt^{N-1}}\)と置くことで、

\[ \begin{aligned} \frac{dx_1}{dt} &= x_2 \\ \frac{dx_2}{dt} &= x_3 \\ \vdots \\ \frac{dx_{N-1}}{dt} &= x_N\\ \frac{dx_N}{dt} &= F(x_1,x_2,\dots,x_{N},t) \end{aligned} \]

と連立常微分方程式として表すことができます。特に、\(F\)が\(t\)に陽に依存しない場合は、自励系（autonomous system）と呼ばれます。

この議論を逆にたどれば、この形の連立常微分方程式は、陽に表された高階常微分方程式として表すこともできます。

特に、\(F\)が\(x\)とその微分について線形であるとき、\(F=a_{N-1}(t) \frac{dx^{N-1}}{dt^{N-1}}+\cdots +a_1(t)\frac{dx}{dt}+a_0 (t) x\)を考えてみましょう。このとき、連立形の方程式は

\[ \begin{aligned} \begin{pmatrix} \frac{dx_1}{dt}\\ \frac{dx_2}{dt} \\ \vdots\\ \frac{dx_{N-1}}{dt}\\ \frac{dx_N}{dt} \end{pmatrix} =\begin{pmatrix} 0 &1&0 &\cdots &0\\ 0&0 &1& \cdots&0\\ \vdots &&\vdots \\ 0&0&0&\cdots &1 \\ a_0(t)&a_1(t) &a_2(t) &\cdots& a_{N-1}(t)\end{pmatrix} \begin{pmatrix}x_1\\x_2 \\ \vdots \\ x_{N-1} \\ x_N\end{pmatrix}\end{aligned} \]

となり、\(x=(x_1,\dots,x_N)\)とベクトルでまとめれば

\[ \begin{aligned}\frac{dx}{dt}= A(t)x\end{aligned} \]

と表せます。つまり、連立形の線形常微分方程式ですね。

以上、高階常微分方程式の連立形への書き換えについて紹介してきました。

特に頻出するのは、2階常微分方程式を2次元の連立微分方程式、平面の力学系として捉えるケースです。1次元的な運動の話でも、相図は平面となるわけです。

高階の常微分方程式の話と、力学系の話は今回のような形では読み替えられるので、驚かずに今回の話を思い出してみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。