どうも、木村(@kimu3_slime)です。
今回は、1次元の線形力学系とは何か、相図の書き方、安定性について紹介します。
1次元の線形力学系とは
一般に、\(A\)を\(N\)次の正方行列として、
\[ \begin{aligned}\frac{dx}{dt}(x) = Ax(t)\end{aligned} \]
\[ \begin{aligned}x(0)=x_0\end{aligned} \]
と表される未知関数\(x(t)\)に関する微分方程式を、線形力学系(linear dynamical sytem)と呼びます。
今回考えるのはその最も単純なケース、\(N=1\)のときです。行列\(A\)は単なる実数\(a\)となり、
\[ \begin{aligned}\frac{dx}{dt}(t) = ax(t)\end{aligned} \]
\[ \begin{aligned}x(0)=x_0\end{aligned} \]
と表される微分方程式が、1次元の線形力学系です。同次形の1階線形微分方程式と言っても良いでしょう。
例えば、マルサスの法則や、ニュートンの冷却法則の微分方程式(\(T_s=0\)のケース)は、1次元の線形力学系です。
参考:人類は必ず食糧問題に直面する? マルサスの法則と微分方程式、ニュートンの冷却法則とは:意味と解き方
相図の書き方
さまざまな初期値\(x_0 \)に対し、そこから出発した解はどのように変化するのでしょうか。それを表すのが相図(phase portrait)、ベクトル場(vector field)という考え方です。
幾何学的に解の挙動を調べる方法は、質的な方法(qualitative method)、力学系(dynamical system)とも呼ばれます。
参考:方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門
1次元の問題の場合、初期値の可能性は実数全体\(\mathbb{R}\)なので、舞台として数直線を考えます。相図は、その数直線上の点\(x_0\)に、変化の方向\(ax_0\)を表す矢印(ベクトル)を書き加えたものです。
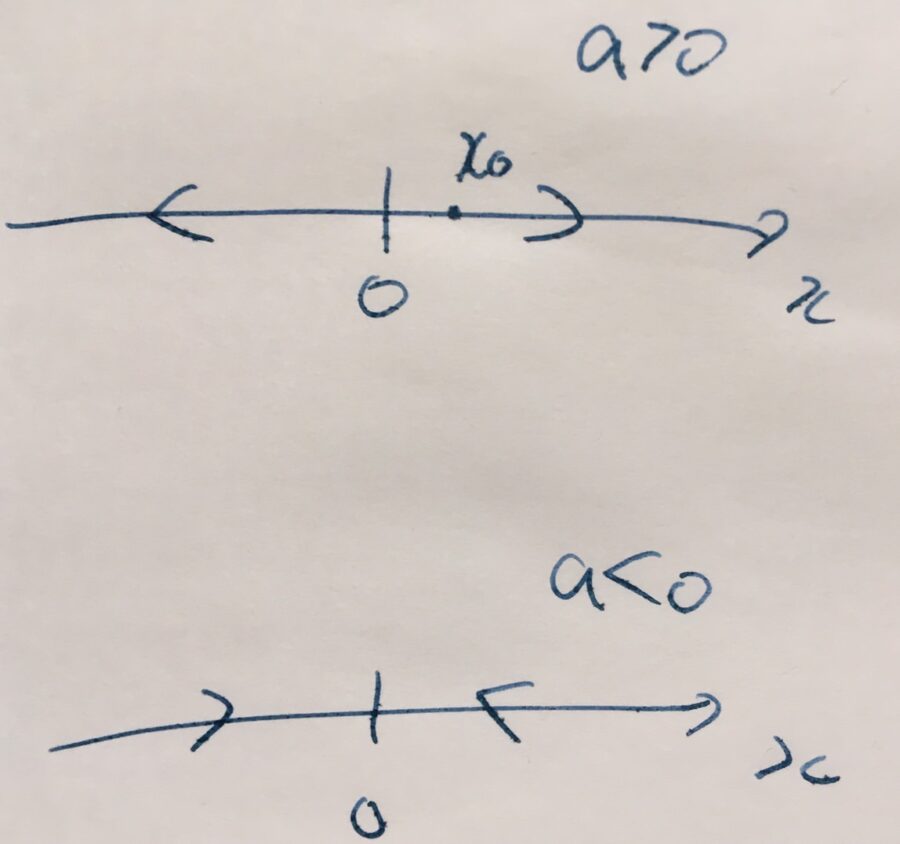
\(a\)が正か負かによって、様子が変わってきます。
\(a\)が正で、初期値\(x_0\)も正のとき、\(ax_0\)も正なのでその点では右向きの矢印となります。原点から離れるほどベクトルは大きくなるわけですが、簡略化としてひとつの矢印で代表させました。各点でどの方向に向かうかが大事です。初期値\(x_0\)が負のとき、\(ax_0\)は負なので、原点から左側では負の方向の矢印を書くことになります。
\(a\)が負のときは、正負の矢印が逆向きになりますね。確かめてみてください。
2次元の力学系では、相図は相平面とも呼ばれます。1次元の例では、相直線(phase line)とも呼べるでしょう。
1階の線形微分方程式は、簡単に解くことができて、
\[ \begin{aligned}x(t) = x_0 e^{at}\end{aligned} \]
となることが知られています。
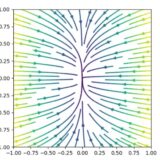
さまざまな初期値\(x_0\)に対し、解\(x(t)\)のグラフを\(t,x\)平面に描くと、次のようになりますね。
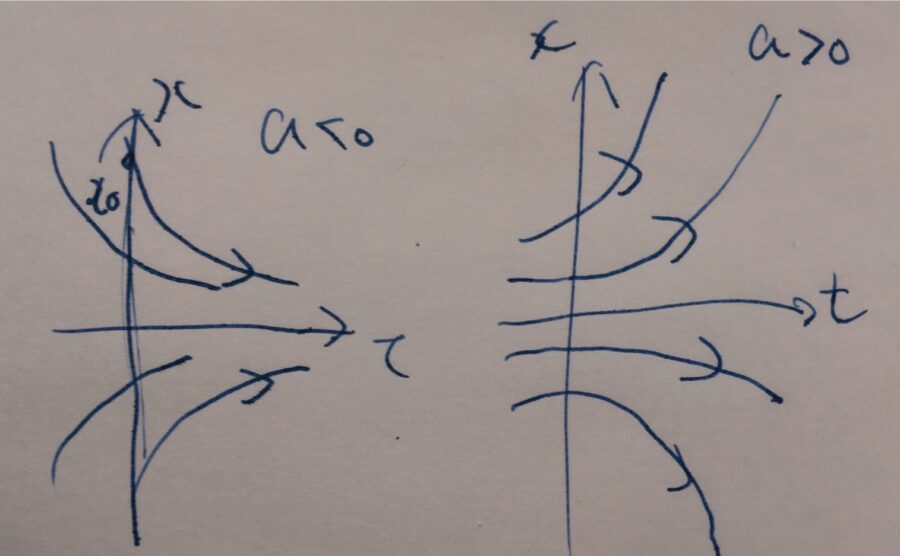
通常の解のグラフと異なり、相図では時間\(t\)を軸とすることはなく、相図上に矢印で時間変化の方向を表すことにしています。だから、グラフのように平面ではなく、ひとつの直線(1次元)として表せているわけですね。これが相図と解のグラフの違いです。
解の安定性
さて、線形力学系(同次の線形微分方程式)には、時間変化しない特殊な解が存在します。\(x(t):=0\)がそうですね。
時間変化しない解は、平衡解(equilibrium solution)、臨界点(critical point)と呼ばれます。
相図の特徴をつかむには、平衡解の安定性(stability)と呼ばれる性質を調べると良いでしょう。
他の初期値から出発した解がすべて平衡解に近づいていくとき、平衡解は(漸近)安定であると呼ばれます。一方、平衡解の近くに平衡解に近づいていかない解が存在するとき、平衡解は安定でない(不安定)と呼ばれます。

参考:方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門、線形微分方程式の解の安定性は「固有値」を調べればわかる
相図を使うと、平衡解の安定性が直観的に判別できます。

\(a>0\)のとき、\(x_0 \neq 0\)である解は、すべて原点から離れていく方向へ変化していきます。したがって、平衡解は安定ではありません。
\(a<0\)のとき、\(x_0 \neq 0\)である解は、すべて原点に近づいていきます。したがって、平衡解は(漸近)安定です。
このような推論は、実際正しいです。今回は簡単に解の表示式
\[ \begin{aligned}x(t) = x_0 e^{at}\end{aligned} \]
が得られています。\(a>0\)のときは\(\lim _{t \to \infty}x(t)\)は発散し、\(a<0\)のときは\(0\)に収束しますね。
ここまで\(a=0\)のケースを考えませんでしたが、そのときはすべての解が時間変化せず、すべての解が平衡解です。\(x(t)=0\)付近の解を考えると、近づきもせず離れもしないもので、このときはリアプノフ安定と呼ばれるものです。
線形力学系の平衡解の安定性は、それを定義する行列の固有値によって判別できることが知られています。
定理
固有値の実部がすべて非正ならば、リアプノフ安定
固有値の実部がすべて負ならば、漸近安定
ある固有値の実部が正ならば、不安定
参考:線形微分方程式の解の安定性は「固有値」を調べればわかる
1次元の力学系では、\(1,1\)行列\(A=(a)\)の固有値は\(a\)そのものです。\(a>0\)のときは不安定、\(a<0\)のときは不安定という結果は、正しく対応していますね。
以上、1次元の線形力学系とは何か、相図の書き方、安定性について紹介してきました。
相図を書くだけで解の全体的な挙動、安定性が判定できるのは便利ですね。2次元の力学系が理解しにくければ、まずは1次元のケースを理解してみると良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
こちらもおすすめ
惑星の運動は数学的に「解けない」? 多体問題から力学系理論へ
方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門