水の流出現象、トリチェリの法則とは：微分方程式を解く

どうも、木村（@kimu3_slime）です。

今回は、水の流出現象を説明するトリチェリの法則について紹介し、その微分方程式を解いていきます。

水の入った水槽やタンクの小さな穴から、重力によって水が流れ出ていく状況を考えましょう。いわば水漏れです。

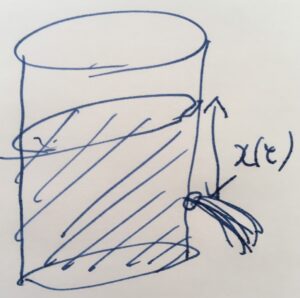
時間\(t\)における水面の高さを\(x(t)\)としましょう。このとき、その時間変化は次のような関係で定式化できることが知られています。

\[ \begin{aligned}\frac{dx}{dt}=- k\sqrt{x(t)}\end{aligned} \]この関係は、トリチェリの法則（Torricelli’s law）、またはトリチェリの定理と呼ばれています。定数\(k>0\)は、重力加速度\(g\)を含み、タンクの断面積、穴の断面積に依存するものです。

水面の高さが高いほど水は速く流れ出していくわけですが、それが速さが高さの平方根に比例するような形ですね。

トリチェリの法則は、流体力学（ベルヌーイの原理）から導出できることが知られています。単純化された式（非圧縮性流体で、粘性を無視している）なので、実験との誤差は少しあるようですが。

さて、トリチェリの法則の微分方程式

\[ \begin{aligned}\frac{dx}{dt}= -k\sqrt{x(t)}\end{aligned} \]

を解いてみましょう。これは変数分離形です。

両辺を\(\sqrt{x(t)}\)で割ると

\[ \begin{aligned} \frac{1}{\sqrt{x}} \frac{dx}{dt}=-k \end{aligned} \]

で、両辺を\(t\)について積分すれば、

\[ \begin{aligned} \int \frac{1}{\sqrt{x}} dx= \int -kdt\end{aligned} \]

です。原始関数を使って積分を計算すると、

\[ \begin{aligned} 2 \sqrt{x} =- kt+C\end{aligned} \]

\[ \begin{aligned}x(t) = \frac{1}{4} (C- kt)^2\end{aligned} \]

となりました。\(x(0)=x_0 >0\)を初期値とすると、

\[ \begin{aligned} x(t)&= \frac{1}{4}(2\sqrt{x_0}- kt)^2\end{aligned} \]

微分方程式の解が得られました。

この解の表示式

\[ \begin{aligned} x(t)&= \frac{1}{4}(2\sqrt{x_0}- kt)^2\end{aligned} \]

は、少し変に見えます。これは放物線であり、\(t\)が大きくなると増加してしまう、水が増えてしまうことになってしまいます。

実際は、ある時刻で\(x(T)=0\)となれば、そのまま\(x(t)=0\)となるはずです。\(2\sqrt{x_0}-kT=0\)を解くと、\(T= \frac{2\sqrt{x_0}}{k}\)となります。したがって、

\[ \begin{aligned}x(t)= \begin{cases}\frac{1}{4}(2\sqrt{x_0}- kt)^2 & (0 \leq t \leq \frac{2\sqrt{x_0}}{k} )\\0 & (t >\frac{2\sqrt{x_0}}{k})\end{cases}\end{aligned} \]

と解を選ぶと良いでしょう。

多くの問題では初期値問題の解は一意ですが、今回の方程式は初期条件\(x(0)=0\)を満たす解は一意ではありません。

参考：微分方程式の解の存在と一意性が成り立たない例

以上、水の流出現象を説明するトリチェリの法則について、微分方程式の解き方を交えて紹介してきました。

時間の2乗に比例して水面が下がっていくような現象を見たら、トリチェリの法則・微分方程式を思い出すと良いでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。