関数列の各点収束、一様収束とは、例と違い、求め方

どうも、木村（@kimu3_slime）です。

今回は、上限の考え方の応用として、関数列の各点収束、一様収束とは何か、例と違い、求め方を紹介します。

関数列、各点収束とは
一様収束とは
こちらもおすすめ

関数列、各点収束とは

扱う対象は、関数の列、関数列\((f_n)_{n \in \mathbb{N}}\)です。

といっても、最初のうちはイメージしにくいかもしれません。極端な話、\(n,x\)を含むような関数を考えれば、関数列となります。

例えば、\(f_n (x):= \frac{1}{n}x\)としましょう。各自然数\(n \in \mathbb{N}\)に対し、\(f\)は実数値関数です。\(n=1,2,3\)とすると、\(f_1(x)=x\)、\(f_2 (x)= \frac{1}{2}x\)、\(f_3(x)= \frac{1}{3}x\)と傾きが下がっていく関数列があるのがわかりますね。

2つの変数を持つ関数ならば、2変数関数とどこが違うのか、と思うかも知れません。関数列と呼ぶときは、一方の変数\(x\)についての1変数関数であり、\(n\)をその関数を変化させるパラメータとして見ています。特に、\(n\to \infty\)と大きくしたときに、その関数列はどんな極限に近づくか、といった問題を考えたいです。

\(f_n (x):= \frac{1}{n}x\)を\(n \to \infty\)としたときの極限は、どう考えれば良いでしょうか。

最も単純な考え方は、各点\(x\)における値\(f_n (x)\)において、そのまま\(n\to \infty\)とする極限を考えることです。

今回の例ならば、まず\(x\)を任意の実数として「固定」します。その上で、\(n \to \infty\)の極限を考えれば、\(\lim_{n\to \infty}\frac{1}{n}x = 0\)です。したがって、\(f(x)=0\)という常に0の値を取る関数に収束すると考えられます。

このように、関数列\((f_n)\)に対して、各点\(x\)で\(\lim_{n\to \infty}f_n (x) =f(x)\)を満たすような関数\(f\)が存在するとき、\(f_n\)は\(f\)に各点収束する（pointwise convergence）と呼びます。

一様収束とは

各点収束は素朴で扱いやすいものですが、「連続関数列の収束」という意味では、より強い収束を考える必要が出てきます。

定義域を\([0,1]=\{x \in \mathbb{R} \mid 0 \leq x \leq1\}\)として、\(f_n(x)=x^n\)という連続関数の関数列を考えてみましょう。

\(f_1(x)=x\)、\(f_2(x)=x^2\)、\(f_3 (x)= x^3\)と、どんどんべきが強くなっていく関数列です。\(0\leq x <1\)の部分では、べきの回数が増えるほどその値は小さくなり、グラフも下側に来るようになります。

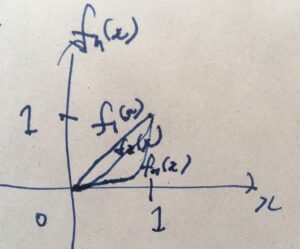
各点収束の極限を求めると、

\[ \begin{aligned}f(x)= \begin{cases}0 & (0 \leq x <1 )\\1 & (x=1)\end{cases}\end{aligned} \]

となります。実際、\(0 \leq x <1\)のときは\(\lim _{n \to \infty} x^n = 0\)であり、\(x=1\)のときは\(\lim_{n \to \infty} 1 = 1\)なので。関数\(f\)は連続関数ではありません。

各点収束という条件では、連続関数列の極限が連続関数とは限らなくなってしまいます（非連続な関数に収束することがある）。

定義

そこで、「連続関数列の極限が連続となる」ような収束の仕方を考えることができます。それが一様収束です。

区間\(I\)上で定義された関数列\((f_n)\)が関数\(f\)に一様収束する（uniform convergence）とは、差の上限が0に収束すること \(\lim_{n\to \infty}\sup _{x \in I} |f_n(x) -f(x)| =0\) です。

各点収束するが、一様収束しない例

さきほどの例で、一様収束がどういう意味なのか考えてみましょう。

一様収束について考えるときは、関数列と極限関数の差の上限を求めます。

難しければ、まずは\(n=1\)のときを考えてみましょう。\(\sup _{x \in [0,1 ] }| f_1(x)-f|=1\)となることが示せます。

なぜか。\(x=1\)では\(f_n(x)=f(x)=1\)なので、その差は0なので考えなくて良いでしょう。その他の点での差の大きさは、\(|f_1(x)-f|=x\)となります。つまり、\(\sup _{x \in [0,1)}x \)を求める問題です。\(x\)を動かしてみると、どうやら1に限りなく近い値を取りそうです。\(x \in [0,1)\)のとき、\(x \leq 1\)なので、\(1\)は上界です。そして、\(L<1\)を満たす任意の実数\(L\)に対し、\(x= \frac{L+1}{2}\)を考えれば、\(L<x\)となります。よって、\(\sup _{x \in [0,1)} x =1\)がわかりました。

同様にして、すべての\(n\)に対して、\(\sup _{x \in [0,1 ] }| f_n(x)-f|=1\)です。よって、\(\lim _{n \to \infty} \sup _{x \in [0,1]}|f_n(x)-f(x)|=1\)で、\(f\)に一様収束しないことがわかりました。

この関数列は、各点収束するが、一様収束しない例と言えます。

「連続関数列の一様収束による極限関数は連続である」という事実が成り立ちますが、逆は一般には成り立たないわけですね。

一様収束では、「関数列と極限の差が一番大きいところが0になるか？」という全体的な見方をしています。一番大きくなっている部分を見るために、上限という道具を使いました。

それに対し、各点収束では全体としての収束状況を気にしません。ひとくちに収束といっても、関数列によっては収束の速い場所と遅い場所があります。たとえばさきほどの例ならば、\(0.9<x<1\)の範囲では、各点で0に収束するものの\(x=1\)での値に引きずられ収束が遅いです。上限として見ればいつまでも差が1になるので、全体としては一様に\(f\)に収束しているとは言えない、というわけですね。

一様収束は定義域が大事

関数列\(f_n (x)= \frac{1}{n}x\)は、区間\([0,1]\)において、\(f(x)=0\)に各点収束していて、かつ一様収束もしています。上限は\(\sup_{x \in [0,1]}| f_n(x)-f(x)|= \frac{1}{n}\)なので、\(\lim_{n\to \infty}\sup_{x \in [0,1]}| f_n(x)-f(x)| =0\)ですね。

一様収束について考えるときは、「～～において」という考える範囲・定義域が大事です。

この例は、\(\mathbb{R}\)全体においては一様収束していません。なぜなら、無限に広い範囲を考えているので、上限が存在しない\(\sup _{x \in \mathbb{R}} |f_n (x)-f(x)| =\infty\)ので。

ただし、任意の有界閉集合上では一様収束しています。一般に、区間\(I\)の任意の有界閉集合（コンパクト集合）上で一様収束することを、コンパクト収束（compact convergence）、広義一様収束（uniform convergence on compact sets）と呼びます。

イプシロンデルタによる言い換え

各点収束と一様収束の違いを、極限の定義（イプシロンデルタ）にまでさかのぼって確認してみましょう。論理記号を使います。

区間\(I\)上の各点収束\(\lim _{n \to \infty}f_n (x)=f(x)\)は、

\[ \begin{aligned}(\forall x \in I)(\forall \varepsilon > 0 )(\exists N \in \mathbb{N}) \\ (\forall n \in \mathbb{N})( n \geq N \Rightarrow |f_n(x)-f(x)|< \varepsilon)\end{aligned} \]

で、一様収束\(\lim_{n\to \infty}\sup _{x \in I} |f_n(x) -f(x)| =0\) は

\[ \begin{aligned}(\forall \varepsilon > 0 )(\exists N \in \mathbb{N}) (\forall n \in \mathbb{N})\\( n \geq N \Rightarrow \sup_{x \in I}|f_n(x)-f(x)|< \varepsilon)\end{aligned} \]

\[ \begin{aligned}(\forall \varepsilon > 0 )(\exists N \in \mathbb{N}) (\forall n \in \mathbb{N})\\(\forall x \in I)( n \geq N \Rightarrow |f_n(x)-f(x)|< \varepsilon)\end{aligned} \]

です。

番号\(N\)の選び方に対する厳しさが両者では違っています。各点収束では、\(N\)は各点\(x\)ごとに選ぶことができます。一様収束ではそれはできず、すべての\(x\)に対して一様に効くような\(N\)の選び方、\(x\)を使わない・依存しない\(N\)の取り方が求められていますね。

これらの条件を見比べることで、一様収束しているならば各点収束していることがわかります。

一様収束のメリット

一様収束という言葉は、関数の上限ノルム

\[ \begin{aligned}\|f\| := \sup _{x \in I} |f(x)|\end{aligned} \]

に関する収束と言えます。つまり、連続関数列\((f_n)\)が\(f\)に一様収束するとは、

\[ \begin{aligned}\lim_{n\to \infty} \|f_n -f\|=0\end{aligned} \]

が成り立つことです。

連続関数列の収束を考えるときは、その極限が連続関数となるような収束、すなわち一様収束、一様ノルムによる収束を考えると扱いやすいです。

例えば、有界な閉区間上の連続関数は、必ず多項式関数によって一様に近似できることが知られています。この「一様に」という言葉の意味を知るには、一様収束を知っておく必要があるでしょう。

参考：稠密性とは：有理数、ワイエルシュトラスの近似定理を例に

また、一様収束しているならば、項別積分や項別微分（極限の順序交換）ができるというメリットがあります。

例えば偏微分方程式の解の候補を、三角関数の級数として表せた\(u(x,t)= \sum _{n=1} ^\infty c_n e^{-n^2 \pi^2 t} \sin n\pi x\)としましょう。この級数が実際に解であることを確かめるには、級数という極限と微分という極限の順序交換ができるか確かめなければなりません。その十分条件として、一様収束は役立ちます。

参考：熱方程式の解き方：変数分離法、フーリエ級数展開（1次元、有界領域）

一般に、関数を項とする級数\(\sum _{k=1}^n f_k(x)\)を関数項級数と呼び、それは関数列の一種です。その一様収束を調べる十分条件としては、ワイエルシュトラスのMテストと呼ばれる方法が有名です。

以上、関数列の各点収束、一様収束とは何か、例と違い、求め方、意義などを紹介してきました。

「違いが一番大きい部分を考える」のが一様収束のイメージです。イメージから先に進むのは難しいですが、簡単な例で良いので、上限や収束の議論に納得できるような説明ができると良いでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。