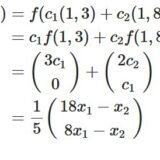どうも、木村(@kimu3_slime)です。
今回は、線形写像の表現行列の求め方を解説します。
前提知識:線形代数における座標・成分・基底とは何か、線形写像、表現行列をなぜ学ぶか:同型写像の考え方
線形写像の表現行列の求め方
表現行列とは
\(V,W\)を有限次元の線形空間とし、\(f:V \to W\)を線形写像とします。\(V\)の基底を\(S=\{v_1,\dots, v_n\}\)、\(W\)の基底を\(T=\{w_1,\dots,w_m\}\)とします。
基底\(S,T\)に関する\(f\)の表現行列\(A_f\)とは、
\[ \begin{aligned}[f(x)]_T =A_f [x]_S\end{aligned} \]
を満たす行列のことです。ただし、左辺は行き先の基底で座標を表し、右辺は行く前の基底で座標を表しています。
具体的に言えば、次のような手順で求められます。基底を使って、\(x= x_1 v_1+\cdots+x_n v_n\)、\(f(x) =y_1w_1+\cdots +y_m w_m\)と表しましょう。その係数\(x,y\)について、
\[ \begin{aligned} \begin{pmatrix} y_1\\y_2 \\ \vdots \\ y_m \end{pmatrix} = A_f \begin{pmatrix} x_1\\x_2 \\ \vdots \\ x_n \end{pmatrix}\end{aligned} \]
を満たす行列が表現行列です。
\(f\)が線形写像であることから、\(y_1,\dots,y_m\)を\(x_1,\dots,x_n\)によって表すことができます。すると、\(f(x)=Ax\)という形の式が得られ、\(A\)が定まるわけです。
例1
\(V=W = \mathbb{R}^2\)、両者に標準基底\(e_1,e_2\)を考えたとき、線形写像\(f(x) =(5x_1+2x_2,x_1)\)の表現行列を求めてみましょう。
まず、インプットを\(x= x_1 e_1 +x_2 e_2\)と\(V\)の基底で表します。また、アウトプットも\(f(x)=(5x_1+2x_2)e_1+x_1e_2\)と\(W\)の基底で表せます。
表現行列とは、\(f(x) =A_f x\)、つまり\((5x_1+2x_2)e_1+x_1e_2 = A_f(x_1 e_1 +x_2 e_2)\)を満たす行列のことです。左辺を成分を使って整理していけば、
\[ \begin{aligned} \begin{pmatrix} 5x_1+2x_2\\2x_2 \end{pmatrix} &= \begin{pmatrix} 5 &2\\0&2 \end{pmatrix} \begin{pmatrix} x_1\\x_2 \end{pmatrix} \end{aligned} \]
と表せます。よって、
\[ \begin{aligned}A_f =\begin{pmatrix} 5 &2\\0&2 \end{pmatrix} \end{aligned} \]
が\(f\)の表現行列として求められました。
「標準基底に関する」線形写像の表現行列は、\(f(x)=Ax\)の形にするだけで求められます。
例2
\(V= \mathbb{R}^2\)、\(W= \mathbb{R}^3\)、\(f:V \to W\)を\(f(e_1)=(1,5,2)\)、\(f(e_2)= (6,2,9)\)により定まる線形写像とします。\(V,W\)の標準基底に関する\(f\)の表現行列を求めてみましょう。
(一般に、基底の行き先が決まるだけで、線形写像はただひとつに定まります。)
標準基底に関する表現行列なので、\(f(x) =Ax\)を満たす\(A\)を求めれば良いです。\(f\)の定義より、
\[ \begin{aligned}f(e_1) =Ae_1 = \begin{pmatrix}1 \\5\\ 2 \end{pmatrix}\end{aligned} \]
\[ \begin{aligned}f(e_2) =Ae_2 = \begin{pmatrix}6 \\2\\ 9 \end{pmatrix}\end{aligned} \]
\(Ae_1,Ae_2\)は、\(A\)の1番目の列ベクトル、2番目の列ベクトルに等しいです。すなわち、
\[ \begin{aligned}A= \begin{pmatrix} 1&6 \\5&2\\ 2&9 \end{pmatrix}\end{aligned} \]
とすれば、\(f(x)=Ax\)を満たします。実際、\(f(x)=f(x_1e_1+x_2e_2)=x_1 f(e_1)+x_2 f(e_2)\)、\(=x_1 Ae_1 +x_2 Ae_2=A(x_1e_1+x_2e_2)=Ax\)なので。よって、\(A\)は\(f\)の表現行列です。
例3
さて、ここからは\(V,W\)の基底が異なるケースを考えます。
\(V=W= \mathbb{R}^2\)、\(v_1 ,v_2 =e_1,e_2\)(標準基底)、\(w_1 =(1,1),w_2=(-1,1)\)、\(f(x) =x\)の表現行列を求めましょう。
\(x\)を\(V\)の基底で表せば、\(x= x_1 v_1+x_2v_2\)です。
一方、\(f(x)\)を\(W\)の基底で表すと、\(f(x)=Ix =x =y_1w_1+y_2w_2\)です。係数\(y_1,y_2\)を求めれば、
\[ \begin{aligned} \begin{pmatrix} x_1\\x_2 \end{pmatrix}&=y_1 \begin{pmatrix} 1\\ 1\end{pmatrix}+y_2\begin{pmatrix} -1\\ 1\end{pmatrix} \end{aligned} \]
より、\(y_1 = \frac{1}{2}(x_1+x_2)\)、\(y_2 = \frac{1}{2}(-x_1+x_2)\)です。
ここで、\(y= A_f x\)を満たす行列\(A_f\)を求めましょう。
\[ \begin{aligned} \begin{pmatrix} y_1\\y_2 \end{pmatrix}&= \begin{pmatrix} \frac{1}{2}(x_1+x_2)\\ \frac{1}{2}(-x_1+x_2)\end{pmatrix} \\ &= \begin{pmatrix} \frac{1}{2}& \frac{1}{2}\\ -\frac{1}{2}& \frac{1}{2}\end{pmatrix} \begin{pmatrix} x_1\\x_2 \end{pmatrix} \\&=\frac{1}{\sqrt{2}}\begin{pmatrix} \cos (-\frac{\pi}{4})& -\sin(-\frac{\pi}{4})\\ \sin( -\frac{\pi}{4})& \cos( -\frac{\pi}{4})\end{pmatrix} \begin{pmatrix} x_1\\x_2 \end{pmatrix} \end{aligned} \]
なので、求める表現行列は
\[ \begin{aligned}A_f =\frac{1}{\sqrt{2}}\begin{pmatrix} \cos (-\frac{\pi}{4})& -\sin(-\frac{\pi}{4})\\ \sin( -\frac{\pi}{4})& \cos( -\frac{\pi}{4})\end{pmatrix}\end{aligned} \]
です。これは\(\frac{1}{\sqrt{2}}\)倍に縮小し、\(-\frac{\pi}{4}\)だけ回転させる(時計回りに45度)回転行列です。
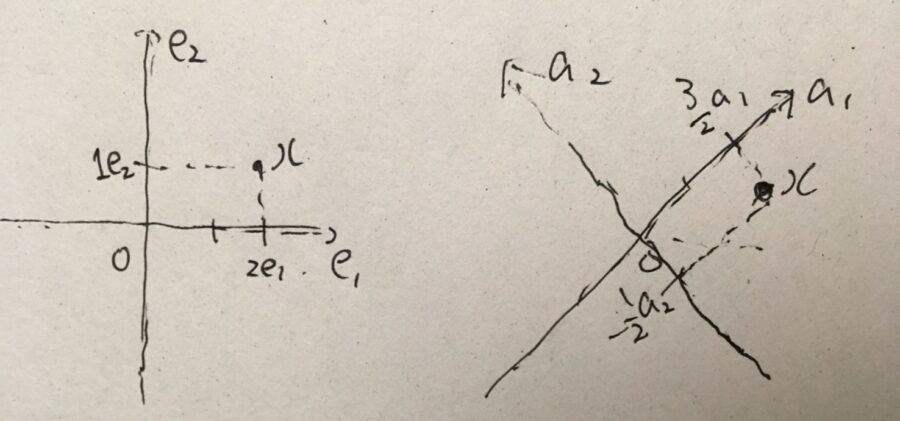
\(f(x)=x\)は、何も動かさない線形写像(恒等変換)です。しかし、行き先の基底を\(w_1 =(1,1),w_2=(-1,1)\)に変えたので、この変換は動いているように見えます。軸が回転して大きな目盛りになったことで、同じベクトルが時計回りに回転し縮んだように見えるわけです。
今回は\(V,W\)で別々の基底を考えましたが、同じ基底を考えれば\(f(x)=x\)の表現行列は単位行列\(I\)となります。(試してみてください)
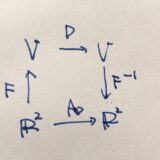
一般に、恒等変換\(f:V\to V,f(x)=x\)の基底\(S=\{v_1,\dots, v_n\}\)から基底\(T=\{w_1,\dots,w_n\}\)への表現行列を、\(S\)から\(T\)への変換行列(transition matrix)、基底の変換(change of basis)と呼びます。
上の例で言えば、\(v_1 ,v_2 =e_1,e_2\)から\(w_1 =(1,1),w_2=(-1,1)\)への基底の変換行列は、\(\frac{1}{\sqrt{2}}\)倍に縮小し、\(-\frac{\pi}{4}\)だけ回転させる行列\(A_f\)です。基底に関して言えば、
\[ \begin{aligned}(w_1,w_2) A_f x =(v_1,v_2) x\end{aligned} \]
なので、
\[ \begin{aligned}A_f = (w_1,w_2)^{-1}(v_1,v_2)\end{aligned} \]
という関係が成り立っています。標準基底を考えていることから\((v_1,v_2)\)は単位行列なので、行き先の基底を行列として\((w_1,w_2)\)考えて、その逆行列を求めることで表現行列\(A_f\)を求められる、とも言えますね。
一般には、\(S=\{v_1,\dots, v_n\}\)から基底\(T=\{w_1,\dots,w_n\}\)への表現行列\(A_f\)は、
\[ \begin{aligned}A_f = (w_1,\dots,w_n)^{-1}(v_1,\dots,v_n)\end{aligned} \]
です。\(S\)が標準基底のとき、\(W=(w_1,\dots,w_n)\)、\(y:=A_f x \)と置くと、\(y= W^{-1}x\)です。
\(A_f x=y=Wx\)ではないことに注意しましょう。軸が反時計回りに回転し拡大すれば、同じ点は時計回りに回転し縮小しているように見えるのです。
例4
少し議論の順序を変えた問題を考えます。
\(f: \mathbb{R}^3 \to \mathbb{R}^2\)、\(f(x_1,x_2,x_3)=(6x_1+2x_2+4x_3,2x_1+2x_3)\)により決まる線形写像を考えます。このとき、表現行列が
\[ \begin{aligned}A_f = \begin{pmatrix} 1&0&0\\0&1 &0 \end{pmatrix}\end{aligned} \]
となるような\(\mathbb{R}^3\)の基底\(a_1,a_2,a_3\)、\(\mathbb{R}^2\)の基底\(b_1,b_2\)を求めましょう。
\(x= x_1a_1+x_2a_2+x_3 a_3\)、\(f(x) =y_1b_1+y_2 b_2\)と表します。表現行列の定義より、
\[ \begin{aligned}y_1b_1+y_2 b_2= \begin{pmatrix} 1&0&0\\0&1 &0 \end{pmatrix}( x_1a_1+x_2a_2+x_3 a_3)\end{aligned} \]
\[ \begin{aligned}(b_1,b_2) \begin{pmatrix} y_1\\y_2 \end{pmatrix}= \begin{pmatrix} 1&0&0\\0&1 &0 \end{pmatrix}( a_1,a_2,a_3) \begin{pmatrix} x_1\\x_2\\ x_3 \end{pmatrix}\end{aligned} \]
なので、
\[ \begin{aligned}\begin{pmatrix} y_1\\y_2 \end{pmatrix}=(b_1,b_2) ^{-1} \begin{pmatrix} 1&0&0\\0&1 &0 \end{pmatrix}( a_1,a_2,a_3) \begin{pmatrix} x_1\\x_2\\ x_3 \end{pmatrix}\end{aligned} \]
です。一方、\(f\)の定義より
\[ \begin{aligned}\begin{pmatrix} y_1\\y_2 \end{pmatrix}=\begin{pmatrix} 6&2&4\\2&0&2 \end{pmatrix} \begin{pmatrix} x_1\\x_2\\ x_3 \end{pmatrix}\end{aligned} \]
です。これらの式を比較すれば、
\[ \begin{aligned}(b_1,b_2)\begin{pmatrix} 6&2&4\\2&0&2 \end{pmatrix}(a_1,a_2,a_3)^{-1}= \begin{pmatrix} 1&0&0\\0&1 &0 \end{pmatrix}\end{aligned} \]
を満たすように\(a_1,a_2,a_3,b_1,b_2\)を求めれば良いです。すなわち、行列の基本変形をすることになります。
\[ \begin{aligned}\begin{pmatrix} \frac{1}{6}&0\\0&\frac{1}{2} \end{pmatrix}\begin{pmatrix} 6&2&4\\2&0&2 \end{pmatrix}=\begin{pmatrix} 1&\frac{1}{3}&\frac{2}{3}\\1&0&1 \end{pmatrix}\end{aligned} \]
\[ \begin{aligned}\begin{pmatrix} 1&0\\-1&1 \end{pmatrix}\begin{pmatrix} 1&\frac{1}{3}&\frac{2}{3}\\1&0&1 \end{pmatrix}=\begin{pmatrix} 1&\frac{1}{3}&\frac{2}{3}\\0&-\frac{1}{3}&\frac{1}{3} \end{pmatrix}\end{aligned} \]
\[ \begin{aligned}\begin{pmatrix} 1&0\\0&-3 \end{pmatrix}\begin{pmatrix} 1&\frac{1}{3}&\frac{2}{3}\\0&-\frac{1}{3}&\frac{1}{3} \end{pmatrix}=\begin{pmatrix} 1&\frac{1}{3}&\frac{2}{3}\\0&1&-1 \end{pmatrix}\end{aligned} \]
\[ \begin{aligned}\begin{pmatrix} 1&-\frac{1}{3}\\0&1 \end{pmatrix}\begin{pmatrix} 1&\frac{1}{3}&\frac{2}{3}\\0&1&-1 \end{pmatrix}=\begin{pmatrix} 1&0&1\\0&1&-1 \end{pmatrix}\end{aligned} \]
\[ \begin{aligned}\begin{pmatrix} 1&0&1\\0&1&-1 \end{pmatrix}\begin{pmatrix} 1&0&-1\\0&1&1\\0&0&1 \end{pmatrix}=\begin{pmatrix} 1&0&0\\0&1&0 \end{pmatrix}\end{aligned} \]
よって、
\[ \begin{aligned} & (b_1,b_2) \\&=\begin{pmatrix} 1&-\frac{1}{3}\\0&1 \end{pmatrix}\begin{pmatrix} 1&0\\0&-3 \end{pmatrix}\begin{pmatrix} 1&0\\-1&1 \end{pmatrix} \begin{pmatrix} \frac{1}{6}&0\\0&\frac{1}{2} \end{pmatrix}\\&=\begin{pmatrix} \frac{1}{6}&\frac{1}{2}\\2&-\frac{3}{2} \end{pmatrix}\end{aligned} \]
\[ \begin{aligned} & (a_1,a_2,a_3) \\&= \begin{pmatrix} 1&0&-1\\0&1&1\\0&0&1 \end{pmatrix}^{-1} \\&= \begin{pmatrix} 1&0&1\\0&1&-1\\0&0&1 \end{pmatrix}\end{aligned} \]
と定めれば、\(f\)の表現行列は
\[ \begin{aligned}A_f = \begin{pmatrix} 1&0&0\\0&1 &0 \end{pmatrix}\end{aligned} \]
となることがわかりました。行列の基本変形とは、線形写像が単純に(標準形に)見えるようにするための基底を探す過程と言えます。
例5
最後に、数ベクトル空間(ユークリッド空間)以外の例を考えます。
\(V=W= P_3(\mathbb{R})\)を3次以下の実係数の多項式のなす線形空間とします。\(D: V\to V\)を\(Df (x)= f^{\prime}(x)\)により定めると、\(D\)は線形写像です(微分作用素)。\(V\)の基底を\(1,x,x^2,x^3\)として、\(D\)の表現行列を求めてみましょう。
まず、インプット\(f\)を基底の線形結合で表せば、\(f(x) =a_0 \cdot1 +a_1x+a_2 x^2+a_3x^3\)です。アウトプットを計算すると、\(Df(x)=f^{\prime}(x)=a_1+2a_2x+3a_3 x^2\)です。
表現行列の定義から、
\[ \begin{aligned}\begin{pmatrix} a_1 \\2a_2 \\3a_3 \\0 \end{pmatrix}=A_D\begin{pmatrix}a_0 \\a_1 \\a_2 \\a_3 \end{pmatrix} \end{aligned} \]
です。これを満たすのは、
\[ \begin{aligned}A_D= \begin{pmatrix} 0&1&0&0\\ 0&0&2&0\\ 0&0&0&3\\ 0&0&0&0 \end{pmatrix}\end{aligned} \]
と求められました。
多項式のなす線形空間であっても、表現行列が実数を成分とする行列として求まるのは、次の理屈によります。
\(P_3(\mathbb{R})\)は4次元であり、\(\mathbb{R}^4\)と同型です。\(e_1,e_2,e_3,e_4\)を\(\mathbb{R}^4\)の標準基底として、\(F: \mathbb{R}^4\to P_3(\mathbb{R})\)を\(F(e_1)=1,F(e_2)=x\)、\(F(e_3)=x^2\)、\(F(e_4)=x^3\)により定まる線形写像とすると、それは同型写像となります。
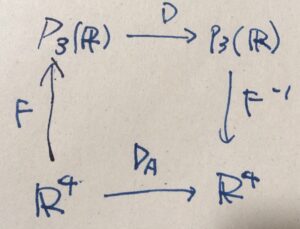
線形変換\(D:P_3(\mathbb{R})\to P_3(\mathbb{R})\)の表現行列とは、\(A_D =F^{-1}\circ D\circ F\)により定まる\(A_D :\mathbb{R}^4 \to \mathbb{R}^4\)のことです。
具体的に求めるには、基底の行き先を計算すれば良いです。
\[ \begin{aligned} A_D e_4 &=(F^{-1}\circ D\circ F)(e_4)\\&= (F^{-1}\circ D) (x^3)\\&= F^{-1}(3x^2)\\&= 3e_3\end{aligned} \]
こうして、\(A_D\)の4列目のベクトルが求められます。他の列も同様です。
以上、線形写像の表現行列、基底の変換の求め方を紹介してきました。
表現行列は、考える基底に依存して定まることが重要です。インプットとアウトプットを基底の線形結合で表すことで、\(y=Ax\)の形から\(A\)を求めるのが基本的な方法となります。
単に\(f(x)=Ax\)と覚えるのではなく(標準基底ならそれで良いのですが)、\(x\)、\(f(x)\)を与えられた基底で表すときの関係式から、表現行列を考えてみましょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
共立出版 (1982-07-09T00:00:01Z)
¥788 (中古品)
世界標準MIT教科書 ストラング:線形代数イントロダクション
近代科学社 (2015-12-22T00:00:01Z)
¥14,721 (コレクター商品)
東京大学出版会 (2019-03-08T00:00:00.000Z)
¥1,870
こちらもおすすめ
線形方程式の解き方:ガウスの消去法と基本変形・ランク、LU分解