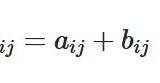対角行列の性質：積、逆行列、固有値について

どうも、木村（@kimu3_slime）です。

線形代数学において、対角行列はシンプルで扱いやすい行列であり、特に行列の対角化において応用されています。

今回は、対角行列とは何か、その性質として、積、逆行列、固有値などについて紹介します。

対角行列の性質
こちらもおすすめ

対角行列の性質

対角行列とは

対角行列（diagonal matrix）とは、正方行列の左上から右下への対角線以外の成分がすべて\(0\)であるような行列です。例えば、行列

\[ \begin{aligned} \begin{pmatrix} 1 &0&0\\0 & -1 & 0 \\ 0& 0 & 3 \end{pmatrix}\end{aligned} \]

は対角行列です。

\(N\)次の正方行列を\(A=(a_{ij})\)と行列の成分を表すとき、\(A\)が対角行列であるとは、\(1\leq i, j \leq N\)として、\(i \neq j\)ならば\(a_{ij} =0\)ということです。

対角行列では、その対角線上のみに数が並びますが、

\[ \begin{aligned}D=\begin{pmatrix} d_1 &0& &O \\ 0& d_2 & & \\ &&\ddots & \\ O & & &d_N \end{pmatrix}\end{aligned} \]

対角線上の成分\(d_1,\dots ,d_N\)を対角成分と呼びます。そこで対角成分を使って、\(D=\mathrm{diag}(d_1,\dots ,d_N)\)と簡単に表記することもあります。

対角行列でない一般の行列に対しても、対角線上の成分\(a_{ii}\)は対角成分と呼ばれます。また、対角線上以外の成分は、非対角成分と呼ばれます。

対角行列というクラスは、次のようなごく簡単な行列を含むものです。

ゼロ行列\(O=\mathrm{diag}(0,\dots, 0)\)は対角行列です。

単位行列\(I=\mathrm{diag}(1,\dots, 1)\)は対角行列です。

単位行列の定数倍\(aI = \mathrm{diag}(a,\dots, a)\)も対角行列です。これはスカラー行列と呼ばれています。

ちなみに、対角線として右上から左下を考えるときは、反対角行列（anti-diagonal matrix）と呼ばれるようです。

和、スカラー倍、積、部分空間

対角行列は多くの演算について「閉じて」いて性質が良いです。

対角行列の和、スカラー倍もまた、対角行列です。

\(A= \mathrm{diag}(a_1,\dots,a_N)\)、\(B= \mathrm{diag}(b_1,\dots,b_N)\)としましょう。

その和は、成分を計算すれば、\(A+B = \mathrm{diag}(a_1+ b_1,\dots,a_N+ b_N)\)と対角行列になります。

そのスカラー倍は、成分を計算して、\( \lambda A = \mathrm{diag}(\lambda a_1,\dots,\lambda a_N)\)と対角行列になります。

和とスカラー倍について閉じていることは、「対角行列のなす集合\(\mathrm{Diag}\)が、行列全体のなす線形空間\(M(N,N)\)において部分空間になっている」とも言いかえられます。

参考：行列全体のなす集合が線形空間（ベクトル空間）となることの証明

さらに、対角行列同士の積もまた、対角行列となります。

行列の積の定義を使って計算すれば、\(AB= \mathrm{diag}(a_1 b_1,\dots,a_N b_N)\)です。行列の積の対角成分は、対角成分の積になっています。

一般に行列の積は順序を変えると結果が変わってしまいますが、対角行列については可換\(AB =BA\)です。\(a_i b_i = b_i a_i\)となるのは、成分＝数（実数、複素数、一般に可換体）が可換であることによります。

また一般に、行列の積というのは計算しにくいものですが、対角行列同士の積は非常に簡単です。特に、同じ行列を何度も掛けること、べき乗が計算しやすい。

\[ \begin{aligned}D=\begin{pmatrix} d_1 &0& &O \\ 0& d_2 & & \\ &&\ddots & \\ O & & &d_N \end{pmatrix}, \quad D^k=\begin{pmatrix} d_1^k &0& &O \\ 0& d_2^k & & \\ &&\ddots & \\ O & & &d_N^k \end{pmatrix}\end{aligned} \]

この計算のしやすさを利用するために、対角行列でない行列を対角行列に変形させる方法（対角化）が生み出されています。

詳しくは：行列の対角化可能性の定義とメリット、例、同値条件について解説

可逆性、逆行列、行列式

対角行列は、どんなときに逆行列を持つ、すなわち可逆（正則）になるでしょうか？

対角行列の積の計算を思い出せば、簡単に逆行列を求めることができます。すなわち、対角行列\(D= \mathrm{diag}(d_1,\dots,d_N)\)は、すべての対角成分が0でない \(d_i \neq 0\) ならば、可逆行列（正則行列）です。

逆行列は\(B= \mathrm{diag}(\frac{1}{d_1}, \dots, \frac{1}{d_N}) \)と、各対角成分をその逆数に置き換えたものになります。実際、\(DB\)を計算すれば、積の計算法則から、対角成分はすべて1となって\(D B = \mathrm{diag}(1,\dots,1)=I\)となるので、\(B=D^{-1}\)です。

行列式は、\(\det D = d_1 d_2 \cdots d_N\)と対角成分の積となります。

これは行列式の定義によればすぐにわかるでしょう。

置換を使った定義\(\det A =\sum _{\sigma \in S_N} \prod _{1\leq i \leq N} \text{sgn}(\sigma) a_{i \sigma(i)}\)なら、1回でも\(0\)がかかるような和の部分は無視できるので、考えるのは恒等置換\(e\)のみになります。結果として\(d_1,\dots ,d_N\)の積しか残りません、\(\det D = \prod _{1\leq i \leq N} \text{sgn}(e) d_{i e(i)} = \prod _{1\leq i \leq N} d_{i}\)。

\(f(a_1,\dots, a_N)=\det A \)と多重線形写像で行列式を定義する流儀で確認します。\(e_i\)を標準的な単位ベクトルとして、単位行列の行列式は1 \(f(e_1,\dots ,e_N)=1\)です。両辺に\(d_1\)をかけて\(f\)の多重線形性を用いれば、\(f(d_1 e_1,e_2,\dots,e_N)= d_1\)。繰り返せば、\(f(d_1 e_1,\dots,d_N e_N)= d_1 d_2 \cdots d_N\)となり、\((d_1 e_1,\dots,d_N e_N)\)に対応するのが対角行列\(D\)です。

対角行列を左上から順に余因子展開していくと、順に対角成分が掛かっていく、と捉えても良いでしょう。

参考：行列式の導出と定義、性質、計算方法（余因子展開）

可逆性には、ほかにいくつかの言い換えがあります。対角行列は単位行列の各行（列）を定数倍したものなので、\(\mathrm{rank} D =N\)とフルランクです。また、各行（列）ベクトルが線形独立なのは、直交しているので見て取れますね。

可逆行列について詳しくは：可逆な行列（正則行列）とは？例と同値な条件

以上の議論は、ブロック対角行列（大きな行列をブロック分けしたときに、その対角部分にしか小行列が並ばない行列）でも同様に行えます。

固有値・トレース

対角行列の固有値は非常にシンプルです。

\(D = \mathrm{diag}(d_1,\dots,d_N)\)ならば、固有値は\(\lambda =d_1,\dots,d_N\)となります。

固有値の定義する式は\(D x = \lambda x , x \neq 0\)ですが、左辺の計算は簡単で\(Dx=(d_1 x_1, \dots ,d_N x_N)\)となります。例えば\(x=e_1=(1,0,\dots,0)\)のときを考えれば、\(De_1 =(d_1,0,\dots, 0)= d_1 e_1\)となり、\(\lambda= d_1\)が固有値、対応する固有ベクトルは\(e_1\)とわかります。同様にして、\(\lambda =d_1,\dots,d_N\)は固有値で、対応する固有ベクトルは例えば\(e_1,\dots, e_N\)です。

対角行列をベクトルの変換として見るとき、対角成分\(d_i\)は\(x_i\)方向への拡大率と言えます。固有値は拡大率のような考え方を反映・一般化させたものになっているわけです。対角行列は、拡大縮小するのみで、回転やせん断をしないような単純な変換と言えます。

参考：線形代数学の応用：CG・画像処理（拡大縮小・反転、回転、せん断）について

「行列の固有値の積は、行列式に常に等しい\(\det A = \lambda _1 \cdots \lambda_N\)」という一般的な性質がありますが、対角行列の場合を考えるとそれが見て取りやすいですね。

参考：なぜ行列式を学ぶのか？固有値・固有ベクトルの求め方：固有多項式の定義

行列のトレース\(\mathrm{tr}A\)とは、対角成分の和のことです。

対角行列の場合は、\(\mathrm{tr}D = d_1 +\cdots +d_N\)と単に対角成分の和を取ったものになりますね。

一般に「トレースは固有値の和に等しい」という性質がありますが、対角行列の場合はそれも明らかになっています。

より広い分類

対角行列を含むような行列の一般的な分類を述べましょう。

対角行列は、対称行列の一種です。行列がその転置行列に等しい、すなわち\(a_{ij} =a_{ji}\)となるとき、対称行列と呼びます。「対称行列は対角化可能」という一般論を学ぶかと思いますが、対称行列は対角行列をより一般化した分類とも見れるわけです。

積の計算しやすさという点では、三角行列があります。対角成分より下側、または上側に成分がない行列は、それぞれ上三角行列・下三角行列と呼ばれるものです。対角行列は、上三角行列でもあり、下三角行列でもあります。

また、対角行列ではその各ベクトルが直交しています。すなわち、対角行列は直交行列の一種です。

参考：直交ベクトルの線形独立性、直交行列について解説

以上、対角行列とは何か、その性質：和や積、逆行列、固有値、他の行列の分類との関連について紹介してきました。

対角行列は一般的な行列と比較すると、単なる数・スカラーに似た都合の良い性質を持っていて、計算がしやすいです。一般的な\(N\)次の行列の例を考えるときにも、単純で扱いやすいでしょう。行列の一般論で迷ったら、まず「対角行列だったらどうなるか？」と考えると、指針が立てやすくなると思います。ぜひ活用してみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。