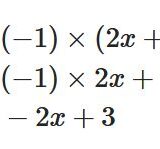どうも、木村(@kimu3_slime)です。
中学校の数学では、平方根やルートについて学びます。しかしその違いについては、よく意識しないと間違いやすいポイントです。
今回は、平方根とルートの違い、ルート外しの注意点を紹介します。
平方根とルートの違い
平方根とルートは、似た状況で使われるため、全く同じ意味だと勘違いされやすいです。
まず、平方根の考え方を紹介しましょう。2乗すると\(9\)になる数はなんでしょうか? その数を\(x\)とすれば、
\[ \begin{aligned}x^2 =9\end{aligned} \]
という方程式を解く問題となります。その解はなんでしょうか? \(x= 3\)はそうですが、\(x=-3\)のことを忘れてはいけません。マイナスかけるマイナスはプラスになるので。この\(x = \pm 3\)の両方を、\(9\)の平方根と呼びます。
このように、平方根はプラスのものとマイナスのもの、2つが必ず存在します。例えば、\(16\)の平方根は、\(4\)と\(-4\)です。
それでも、平方根を簡単な記号で表したい。そこでルート記号が登場します。平方根にはプラスとマイナスの2つがありますが、そのプラスの方をルート記号\(\sqrt{} \)を使って表すのです。例えば、\(\sqrt {9} =3\)、\(\sqrt{16}=4\)となりますね。
じゃあマイナスの平方根はどこへ行ってしまったのかというと、それはマイナスをつけたルート\(-\sqrt{9}= -3\)で表せているのです。平方根は常に2つあり、その正の方をルート記号で表すと、負の方がマイナスルートで表せる。そういう習慣を学ぶのが、平方根とルートの違いを意識する基本です。
ちなみに、平方とは2掛けること、2乗のことです。平方根は、2乗根とも呼ばれます。平方は英語でいうsquare(正方形)の訳語であり、\(x^2\)は\(x\)スクエアと言ったように読まれます。平方根の根(root)とは、方程式の解と同じ意味です。平方により定まる方程式\(x ^2 =9\)の解なので、平方根と呼ばれています。
平方根やルートをなぜ学ぶか。例えばそれは、直角三角形の性質を考えると登場します。
直角三角形の底辺と高さを\(a,b\)、斜辺を\(c\)とすると、\(a^2 +b^2 =c^2\)という関係が常に成り立ちます。これは三平方の定理、ピタゴラスの定理と呼ばれるものです。
具体的に、底辺と高さがそれぞれ\(1,1\)の長さのとき、斜辺\(c\)の長さはどれくらいでしょうか。それは、\(1^2 +1^2 =c^2\)、\(c^2 =2\)を解くことで得られます。
\(c^2 =2\)を解くと、数学的には\(c= \sqrt{2} , -\sqrt{2}\)が得られます。ただし、ここでは長さを考えているので、\(c>0\)という条件が加わり、\(c= \sqrt{2}\)となりました。図形の長さの問題を考えるときには、よく正の平方根を使います。しかし、だからといって平方根=プラスというイメージを持つのは正しくないわけです。
一般に、\(a\)の平方根(square root)とは、\(x ^2 =a\)を満たす数\(x\)のことです。平方根を定める式は、2次方程式なので、解が常に2つあります。
そこで、正の平方根の方を、ルート記号を使って\(\sqrt{a}\)と書きます。するともう一方の平方根は、\(- \sqrt{a}\)と表されるわけです。\((\sqrt{a})^2 =a\)ですし、\((-\sqrt{a})^2 =a\)でもあります。
直角三角形と三平方の定理のように、2次方程式は長さを定める方程式として現れます。他の問題でもいくらでも登場する重要な方程式です。2次方程式は、いつでも解けるようになっていてほしい。\(\sqrt{2}\)という長さは、数として存在していてほしい。
そこで、\(x ^2 =a\)の解を表す数字を、\(x= \sqrt{a},- \sqrt{a}\)と表して、そういう「数」も数の仲間に入れることにする。すると、\(a\)が\(4,9,16\)のような数(整数の二乗で表される数=平方数)でなくても、いつでも2次方程式が解けるようになるわけです。
整数や分数で表されるようキリの良い数だけでなく、そうあらわせない可能性がある\(\sqrt{}\)を含む数の体系は、実数と呼ばれます。\(\sqrt{2}\)は、分数として表せない:無理数であることが知られています。
ルートの外し方と注意点
ルートを含む式を、より簡単に表せるときにはそうしたい、ルートを外す問題を中学校や高校の数学では扱うでしょう。
ルートの単純化のコツは、中身を何かの2乗の形にすることです。例えば、
\[ \begin{aligned} \sqrt{8} &= \sqrt{2^2 \cdot 2 } \\&= \sqrt{2^2} \sqrt{2} \\ &= 2 \sqrt{2} \ \end{aligned} \]
といったように、\(2^2\)をくくりだすことで、\(\sqrt{8} =2 \sqrt{2}\)と表せます。
だからといって、中身が2乗の形になればすぐにルートを外せる、とは思ってはいけません。文字を含むルート、ルートを使った関数の問題では間違いやすいポイントです。例えば、\(x\)を実数とするとき、
\[ \begin{aligned}\sqrt{(x-2)^2}= x-2\end{aligned} \]
は間違いです。2乗のルートだからそこを外せば良いじゃん、と思うでしょうか?
ここで、ルート\(\sqrt{}\)は正の平方根を表している、という定義を思い出しましょう。右辺の\(x-2\)は、例えば\(x= 1\)のとき\(-1\)となります。一方で、左辺は\(\sqrt{(-1)^2}= \sqrt{1}=1\)となります。したがって、\(1= -1\)が導かれて矛盾してしまいました。左辺がルート\(\sqrt{}\)で表されている、つまり正の数である限りは、右辺に負になりうる式が出てきてしまってはおかしいのです。(プラスの)ルートは常に正となるという感覚を養いましょう。
では、文字式を含むルートはどう考えれば良いか。正負によって状況が変わる問題の基本は、場合分けです。この問題では、\(x \geq 2\)か、\(x<2\)かによって状況が変わってきます。
\(x\geq 2\)のときは、\(x -2 \geq 0\)(正)です。このとき、\(x-2\)は2乗すると\((x-2)^2\)になる正の数なので、\(\sqrt{(x-2)^2} =x-2\)です。一方、\(x <2\)のときは、\(2-x =-(x-2)>0\)です。\(-(x-2)\)が正であり、\((- (x-2) )^2 = (x-2)^2\)なので、\(\sqrt{(x-2)^2}=-(x-2) \)となりました。以上をまとめれば、
\[ \begin{aligned}\sqrt{(x-2)^2}= \begin{cases}x-2 & (x \geq 2 )\\-(x-2) & (x<2)\end{cases}\end{aligned} \]
となりました。これは絶対値の記号\(|\cdot |\)を使って、
\[ \begin{aligned}\sqrt{(x-2)^2}= |x-2|\end{aligned} \]
と簡単に表すこともできます。
\(\sqrt{a^2} =a\)が成り立つのは、中身が正のとき\(a \geq 0\)という限定がつくのです。なぜなら、正の平方根がルート記号の定義だからですね。\(a<0\)ならば、\(\sqrt{a^2} =-a\)です。一般的な記号を使えば、\(\sqrt{a^2} =|a|\)となります。
絶対値記号で表せるとまあ知っておくのも役立つのですが、それに先立つ理解がルート記号単体では正の数を表しているという約束を知ることです。
(高校では、ルートの中身が負になるような数、複素数を考えることになるでしょう。\(\sqrt{-1}= i\)は正の数でも負の数でもありません。今回は、ルートの中身が正であるケース、実数を定めるようなルートを考えました。)
以上、平方根とルートの違い、ルート外しの注意点を紹介してきました。
正の数も負の数も二乗すると常に正になるという性質、\(\sqrt{}\)はプラスの平方根を表すことは、意識していないと見逃されやすいです。文字式や関数の分野では、この数はプラスなのかマイナスなのか?という感覚を持つようにすると、間違いを減らせるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
PHP研究所 (2015-03-12T00:00:00.000Z)
¥855