どうも、木村(@kimu3_slime)です。
僕は数学の授業をあまり聞いていませんでしたが、それでも定期テストや受験数学ではある程度良い成績を残すことができました。なぜかといえば、自分ひとりで教科書を読めたからだと思っています。
今回は、中学や高校の数学、受験数学の勉強法として、教科書・参考書の読み方を紹介します。
教科書を読む重要性
僕の勉強に対する考え方として、「授業を聞いているだけで数学ができるようになったら苦労しない」というものがあります。
もちろん、真面目に授業を聞いた結果成績の良い人もいましたが、そうでない人もたくさん見てきました。もちろん、先生の話を聞くことが勉強のマイナスになるとは言いません。しかし、授業を通して「自分の理解が深まるか」が大事なのです。自分にわかることが増えないなら、どんなに真面目な態度であっても、徒労に終わってしまうのではないでしょうか。
僕自身は、授業中はあまり話を聞かず、自分のペースで教科書や参考書を読んでいました。数学という科目は、以前に学んだ分野の知識を常に必要とする積み重ね型の学問です。学校の授業は教科書の順番通りに進んでいきますが、自分がわかっていない知識を前提とした話なら、どんどんわからないことが積み重なっていってしまいます。
定期テストや大学受験においては、当たり前ですが、自分ひとりで問題を解かなくてはなりません。助けになるのは自分の頭脳だけで、先生も教科書もそこにはありません。自分で考えて、できる範囲で問題を回答する、アウトプットする力が求められます。
そのアウトプットの力を培うためには、授業を受動的に受けるだけでなく、自分の理解度に応じて教科書・参考書を自分から読んでいくことが近道ではないでしょうか。
教科書の読み方
「数学の勉強は、教科書を読めばいいって? そんな正論、それこそできたら苦労しない。教科書が難しくて読めないから、必死に授業を聞いているんだ」という意見もあるでしょう。
その気持ちはわかります。ひとりで教科書を読むことは、誰にでもできることではないと、同級生を見ていて思いました。しかしそもそも、読もうとしなければ、読み方を知らなければ読めないものです。今回は、僕なりの教科書・参考書の読み方を紹介します。
ネットで参照できる教科書(テキスト)として、FTEXTの「数学I>三角比>鋭角の三角比」を例として扱いましょう。
簡単な問題を解いて、わからない単元を見つける
(試験)勉強の基本は、「わからないことをわかるようにすること」です。
そのためには、「自分がわかっていないことを、教科書の中から見つけること」が必要になります。
おそらく、自分がわかっていないことに気づくというプロセスが、多くの人にとって難しいのでしょう。全部わからないような気もするし、気持ちではわかってるような気もするし。
「自分がわかっていると思うかどうか」というのは、主観的で、判断基準としては当てになりません。そこで僕がわかっているかのどうかの判定基準にしていたのは、簡単な問題を何も見ずに解けることです。試験におけるアウトプット能力は、問題を解こうとする試みの中で培われます。
数学の教科書や参考書の構成としては、まず定義や概要の説明があって、その後に簡単な問題が必ず提示されています。例えば次の問題が解けるかどうか、ノートに書いてみましょう。
僕がノートに書くならば、心の中でこんなことを考えます。ある角度のタンジェントというのは、その角を左下側に、直角な部分を右下に置いた三角形における、高さを底辺で割った値のことだ(定義の確認)。だから、\(\tan A =\frac{4}{3}\)。\(\tan B\)の方は、三角形がよく見る位置関係とは違ったように描かれているので、注意したい。たぶん、\(4/2 ,2/4\)のどっちか迷わせようとしている問題だ(出題意図の考察)。標準的な形に回転させて書き直すと(回答の導き方)、\(\tan B =\frac{2}{4}\)がわかる。
ここまで書けなくても、何も見ずに自分で回答を書いてみて、それで答え合わせをしてあっていれば、とりあえずは理解していると見て良いでしょう。それなら先に進めば良いです。
問題は、間違っている、または回答がほぼ書けないときの対処法です。回答が全く書けないときは、たぶんタンジェントとは何か、そもそも定義が理解・記憶できていないのだと思います。概要や例を見直しましょう。回答が間違っているときは、タンジェントとは何かなんとなくわかっているものの、正確に理解できていないのでしょう。
これが一番ありがちで、「なんとなくわかっているが、回答を間違えてしまう」段階のものをわかっているとは考えず、「わかっていない」と判断することが大事です。不確実で「できない」ことを受け止めて、それを「できる」段階に持っていくために考えましょう。
わからない単元の克服方法
わからない問題、単元を見つけました。それをわかるようにするには、どうしたら良いのでしょうか。
回答を読むのが、第一の方法です。しかし、日本の数学の教科書にありがちですが、回答がシンプルすぎて、読んでもよくわからないことがあります(笑)。答えの数字は書いてあるけど、どうやってその回答に至ったのかわからないから、自分で問題が解けるようにならない。だから数学は嫌いだ、と。
教科書がわからなければ、参考書と合わせて考えてみましょう。同じような内容でも、書き方が違えば理解できるかもしれません。僕は学校で指定されていた参考書として、黄色チャート(チャート式解法と演習数学I+A)を使っていました。回答に至るための考え方やヒントが書かれていて、教科書よりは親切だったと思います。先生に質問するのも良いでしょう。
良くないが実践されている方法として、「とりあえず回答を写す」というものがあります。だいたい効果がなく、時間の無駄です。なぜなら、理屈がわかっていなければ、ちょっと数字を変えたり、ちょっと応用した問題が解けないので。
回答を自分が納得いくレベルで理解しようとすることが大事です。どうしてそれが答えになるのか、自問自答し、言葉の定義や公式を確認しながら、考えましょう。ひとつの例ではわかりにくいので、教科書や参考書から、類題を探すのが大事です。仲の良い友達と、おしゃべりしている感覚で、今学んでいる内容を説明しようとしてみましょう。どこに自分が納得できていないか、そのプロセスを通じてわかってきます。そうして納得した回答を、(できればお手本を見ずに)書くトレーニングをするのには効果があるでしょう。
縦にさかのぼって読む
「回答を読んで自分で考えても、どうしても納得できないし、全然わからないんだよ」ということもあるかと思います。
わからないことは、全く悪いことではありません。むしろ、勉強においてはプラスです。わからないと自覚することから、学びはスタートするので。
わかるように試行錯誤してもなおわからないと、ちょっとゲンナリしてくるかもしれません。そういうときは、その問題・単元は、一旦保留にします。「今はわからない」とラベルをつけておくわけです。
その後、気分転換に次の単元に進むのも良いですが、基本的には、自分にわかるところまで戻ることをおすすめします。
例えばタンジェントがわからなければ、直角三角形や図形の相似・合同、三平方の定理がわかっていないかもしれません。教科書の前のページ、時には学年をまたいで、自分がどこから苦手意識を感じているのか、振り返ってみましょう。
中学・高校の数学は、おおざっぱに、代数・幾何・解析・統計という4分野にわかれています。1年間の間に、各分野の内容を横に少しずつ学んでいくわけです。しかし前提知識としては、幾何ならば幾何で、1学年前、縦に並んでいたりします。
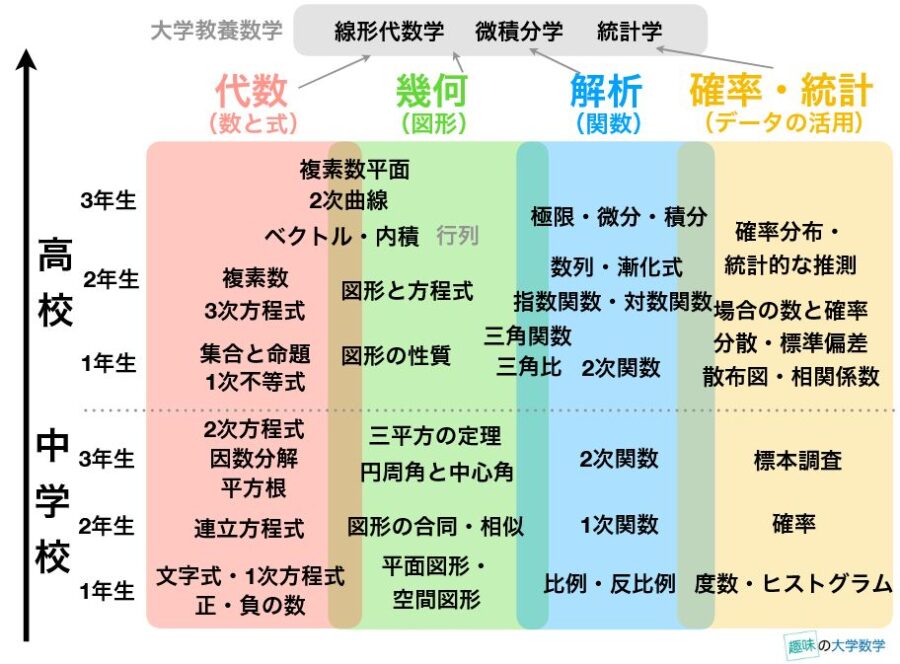
繰り返しますが、中学校や小学校レベルの算数・数学がわからないのは、恥ずかしいことではありません。僕も最近、ひし形と平行四辺形の違いがわかっていないことに気づいて驚きました(笑)。
自分がわかるところまで戻っていって、自信を取り戻しましょう。コツコツと戻っていけば、簡単な問題なら必ず解けるようになります。いきなり難しい内容をショートカットして理解できたら楽だしかっこいいですが、それができたら数学で苦戦はしないでしょう。
そもそも、自分が教科書を読もうとしていなかった、ある時期は勉強をまともにしていなかった、ということもあります(僕は中学生のときそうでした笑)。時間が経ってから教科書を読んでみると、当時はわからなかったことが、わかるようになっている場合もあります。
今の学年より前の内容を理解しても、すぐさまテストの点数に結びつくわけではないでしょう。しかし長期的には、足元を確かにしていったほうが、確実に回答できる問題が増えていきます。何より、確実にわかる部分からちょっとずつ手を付けていくほうが、やっていて楽しいと思います(笑)。
以上、受験数学、中学・高校数学の勉強法として、教科書・参考書を読むことの大切さ、読むときの考え方を紹介してきました。
「テキストを自分ひとりで(正確に効率よく)読解する」ことは、学習において非常に価値が高いです。それができればどんなことも独学できるようになります。その読解力は、大学での学び、人生全体を通して役立つものです。
ポイントは
- 簡単な問題を解いてみて、わからないことを探す
- わからないのはなぜか、本を見ながら自問自答する
- 手を付けられないレベルなら、もっと簡単な内容まで戻っていく
ことです。自分で教科書を読むことにチャレンジして、たとえ高度な問題が解けなくても、自信をもてる問題や分野を見つけてみてはいかがでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
数学Ⅰ 改訂版 [104数研/数Ⅰ327] 文部科学省検定済教科書
数研出版 (2003T)
¥1,272
数研出版 (2019-01-24T00:00:01Z)
¥1,991
こちらもおすすめ
大学数学の教科書(数学書)が難しいのはなぜ? 読み方を考える
大学数学の教科書の読み方、最初に「定義・命題・証明」を知ろう


![数学Ⅰ 改訂版 [104数研/数Ⅰ327] 文部科学省検定済教科書](https://m.media-amazon.com/images/I/41oc5HEPBtL._SL200_.jpg)