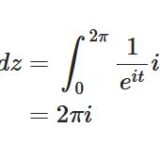コーシーの積分定理とは：積分路の変形、証明

どうも、木村（@kimu3_slime）です。

複素解析におけるシンプルで強力な結果として、コーシーの積分定理があります。

今回は、コーシーの積分定理とは何か、積分路の変形による計算、グリーンの定理による証明を紹介します。

コーシーの積分定理とは
グリーンの定理による導出
こちらもおすすめ

コーシーの積分定理とは

前回、いくつかの複素積分の計算を紹介しました。閉曲線\(c(t)= e^{it}, 0 \leq t \leq 2\pi \)における積分をすると、べき乗\(z^k\)（\(k \neq -1\)）、指数関数、三角関数の積分は0になっていました。

これは偶然ではなく、次のように一般化されます。

コーシーの積分定理（Cauchy’s integral theorem）、コーシー・グルサの定理（Cauchy–Goursat theorem）

\(D\subset \mathbb{C}\)を開集合で、その境界が\(C^1\)級の曲線をつなぎあわせた単純な閉曲線\(c\)によって表されるとする。\(f: D \to \mathbb{C}\)を正則な関数とする。このとき、

\[ \begin{aligned}\int_c f(z) dz =0\end{aligned} \]

が成り立つ。

条件を満たす開集合\(D\)の例としては、三角形や四角形、円などがあります。一般には、「単連結な領域」と呼ばれる条件で成り立つ定理です。

定理の仮定で気をつけたいのは、\(c\)によって囲まれる領域の内部\(D\)で関数が正則であることです。

\(D=\{z \in \mathbb{C} \mid |z| <1\}\)としましょう。\(f(z)=z^k\)は、\(k \geq 0\)のとき、すべての\(z \in \mathbb{C}\)において正則です。したがって、コーシーの積分定理により

\[ \begin{aligned}\int_c z^ k dz=0\end{aligned} \]

と言えます。が、\(k<0\)のときは、\(z=0 \in D\)において正則ではありません。したがって、コーシーの積分定理からは何も言えません。実際、

\[ \begin{aligned}\int_c z^ {-1} dz=2\pi i\end{aligned} \]

です。\(k\leq -2\)のときは

\[ \begin{aligned}\int_c z^ {k} dz=0 \end{aligned} \]

とはなっていますが、これは積分定理による結論ではありません。

積分定理を使えば、いくつかの点（特異点）を除いて正則な関数の複素積分が計算しやすくなります。

\(f(z) =\frac{1}{z} +\frac{1}{z-1}\)を、\(c_2(t) = 2e^{it}\)において積分しましょう。素直に計算しようとすると、\(\frac{1}{z-1}\)の項が面倒です。

積分経路の内部は\(D =\{z \mid |z|<2\}\)で、\(z=0,1\)において\(f(z)\)は正則でなく、それ以外の部分では正則です。

半径\(2\)の円に、\(z=0,1\)で鍵穴を開けたたような経路\(c\)を考えましょう。

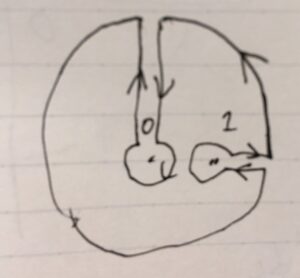
この経路の内部においては、\(f\)は正則なので、コーシーの積分定理より

\[ \begin{aligned}\int_c f(z) dz =0\end{aligned} \]

が成り立ちます。ここで鍵穴に至る経路の幅を小さくした極限を考えましょう。

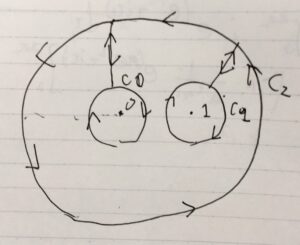
すると、外周から\(z=0,1\)に至る積分は往復するので打ち消し合い、\(c_2\)での積分と、上の図に示した\(c_0,c_1\)での積分が残ります。したがって、さきほどの等式から、

\[ \begin{aligned}\int_{c_2} f(z)dz +\int_{c_0} f(z) dz +\int_{c_1}f(z)dz=0\end{aligned} \]

が成り立ちます。図で示した経路は、具体的には\(c_0(t)= \frac{1}{2} e^{-it}\)、\(c_1(t) =1+\frac{1}{2}e^{-it}\)であったとしましょう。通常の向きとは逆、時計回りにパラメータ付けされていることに注意。

それぞれの経路の内部で、コーシーの積分定理により一方の項の積分が消えることに注意すると、

\[ \begin{aligned}\int_{c_0} f(z) dz = \int_{c_0} \frac{1}{z} dz = – 2\pi i\end{aligned} \]

\[ \begin{aligned}\int_{c_1} f(z) dz = \int_{c_1} \frac{1}{z-1} dz = – 2\pi i\end{aligned} \]

となるので、

\[ \begin{aligned}\int_{c_2} f(z)dz =4 \pi i\end{aligned} \]

であることがわかりました。結局、広い範囲での線積分の結果が、正則でない点を含む円周での積分を足し合わせたものになっています。

コーシーの積分定理によれば、\(f\)が正則である範囲においては積分経路を変えても、結果は同じになるのです。これは積分路変形の原理と呼ばれています。

グリーンの定理による導出

コーシーの積分定理を証明しましょう。

それは、実関数の線積分に関する定理、グリーンの定理によって示すことができます。

\(D\subset \mathbb{R}^2\)を有界な領域で、その境界が\(C^1\)級の曲線をつなぎあわせた閉曲線\(c\)によって表されるとする。\(F:D\to \mathbb{R}^2\)、\(F=(F_1,F_2)\)を\(C^1\)級とする。このとき、次の式が成り立つ。

\[ \begin{aligned}\int _c F = \int _D (-\frac{\partial F_1}{\partial y}+\frac{\partial F_2}{\partial x})dxdy\end{aligned} \]

\(D\),\(c\)は\(\mathbb{C}\),\(\mathbb{R}^2\)で同じ記号を使って、適切に読み替えます。\(f: D \to \mathbb{C}\)を正則関数、\(c:[a,b]\to \mathbb{C}\)とし、\(f(z)=u(x,y)+i v(x,y)\),\(c(t)=x(t)+iy(t)\)と実部と虚部に分けて表しましょう。このとき、複素積分と実線積分の関係は、

\[ \begin{aligned} \int _c f(z)dz &= \int_a^b f(c(t)) c^{\prime}(t)dt \\&= \int_a ^b (u+iv) (x^{\prime }+iy^{\prime})dt \\ &= \int_a ^b (ux^{\prime }-vy^{\prime})dt \\ & + i\int_a ^b (v x^{\prime }+uy^{\prime})dt\\&=\int_c (u,-v) + i\int_c (v,u) \end{aligned} \]

と表されます。ここで\(F=(u,-v)\)と\(G=(v,u)\)にグリーンの定理を用いれば、

\[ \begin{aligned} \int _c f(z)dz &= \int _D (-\frac{\partial u}{\partial y} – \frac{\partial v}{\partial x} dxdy ) \\ &+ i \int _D (-\frac{\partial v}{\partial y} + \frac{\partial u}{\partial x} dxdy )\end{aligned} \]

となります。正則関数は、コーシー・リーマンの方程式

\[ \begin{aligned}\frac{\partial u}{\partial x } =\frac{\partial v}{\partial y}\end{aligned} \]

\[ \begin{aligned}\frac{\partial u}{\partial y }= -\frac{\partial v}{\partial x}\end{aligned} \]

を満たすので、結果としては最後の2項は消え、

\[ \begin{aligned}\int _c f(z)dz =0\end{aligned} \]

とコーシーの積分定理が示されました。

（詳しいことを言うと、グリーンの定理を用いるに当たり、\(f\)の実部、虚部が\(C^1\)級であるという仮定を置いています。その仮定なしにコーシーの積分定理は示せます。例えば、スタイン・シャカルチ「複素解析」や杉浦「解析入門 Ⅱ」を参照。）

以上、コーシーの積分定理とは何か、積分計算への例や、グリーンの定理を用いた導出を紹介してきました。

関数が正則になる領域では、閉曲線上の積分が0になること。したがって、関数が正則である限り、自由に経路を変えても良いこと。正則でない部分を含むような積分なら、個別にそこでの積分を計算すれば良いこと。

コーシーの積分定理が導くこれらの性質はとても便利ですし、コーシーの積分公式や留数定理、他にも多くの結果を導く重要な結果です。関数が「どこで」正則になっているのかに気をつけて、積分定理を使った議論が自由にできるようになってみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。