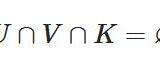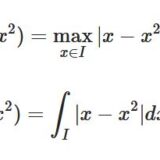どうも、木村(@kimu3_slime)です。
今回は、コンパクト性とはどういうものか、有界閉集合における最大値・最小値の定理を例に紹介します。
最大値・最小値の定理
位相空間論ではコンパクト性という概念がありますが、それは抽象的な考え方です。そこで、今回は最大値・最小値の定理から話を始めます。
高校の数学でも、与えられた関数の最大値・最小値を求めよ、という問題がよくあります。そもそも最大値・最小値が存在していなければその話はできません。
最大値・最小値の定理(extreme value theorem)
\(I\)を有界な閉区間とする\(I=[a,b]\)。\(f: I \to \mathbb{R}\)を連続関数とする。このとき、\(f\)は\(I\)上で最大値、最小値を持つ。
この定理は、中間値の定理と並び微積分において基本的な定理です。平均値の定理やテイラー展開の基礎ともなっている重要な定理と言えます。
この定理のポイントは、定義域\(I\)が有界な閉区間ということです。
\([a,b]=\{x \in \mathbb{R} \mid a \leq x \leq b\}\)です。この集合は有界であり、境界、ここでは端点を含んだ閉集合です。
\([0,\infty)=\{x \in \mathbb{R} \mid 0 \leq x\}\)は無限半閉区間と呼ばれますが、そこで\(f(x)=x\)は最大値を持ちません。どんなに大きな数\(M\)よりも、\(x=M+1\)とすれば\(f(x)>M\)なので。ただし、最小値は存在して、\(0\)ですね。定義域が無限の大きさを持つ(有界でない)と、最大値最小値を持たないケースが起こり得ます。
\((0,1]\)という半開区間で、\(f(x)=\frac{1}{x}\)を考えます。\(f\)は最小値\(1\)を持ちますが、最大値を持ちません。原点に近づくにつれ限りなく大きな値を取りますね。\(f(0)=0\)と適当に値を定義した関数\(f\)を考えることはできますが、そうすると\([0,1]\)有界な閉区間での関数になりますが、\(f\)は連続にはなりません。定義域が端っこまで閉じたケースでないと、その開いた部分で最大値・最小値を取れないケースもありえますね。
最大値・最小値の定理は、それらが存在するための十分条件を与えるに過ぎないことに注意しましょう。有界でない区間においても、最大値や最小値が存在するケースはあります。例えば、定数関数や三角関数など。
コンパクト性とは
今回は実数\(\mathbb{R}\)の区間における最大値の定理を考えましたが、ユークリッド空間\(\mathbb{R}^N\)の有界な閉集合においても同様の主張が成り立ちます。
有界な閉集合とはどういうものか、おさらいしておきましょう。
例えば、\(D:=[0,1]\times [0,1] \subset \mathbb{R}^2\)は有界な閉集合です。そこで連続な関数\(f(x,y)=x^2+y^2\)は最大値\(2\)、最小値\(0\)を持っています。
部分集合\(D \subset \mathbb{R}^N\)が有界である(bounded)とは、\(D\)がある(大きな)開球\(B_N(0,r):=\{x \in \mathbb{R}^N \mid \|x\| \leq r\}\)に含まれること\(D \subset B_N(r)\)です。
部分集合\(D\)が閉集合であるとは、補集合\(\mathbb{R}^N \backslash D\)が開集合であることです。\(U\)が開集合であるとは、そのすべての点\(x\in U\)に対し、(小さな)開球\(B(x,r)\)で、\(B(x,r) \subset U\)となるものが存在することでした。
閉集合は、境界点をすべて含む集合である、とも言えます。
詳しくは:ユークリッド空間の開集合、閉集合、開球、近傍とは何か?
さらには、有界な閉集合という性質は、コンパクトな集合として一般化されます。
そのために、ある集合を複数の集合で覆うこと、開被覆という考え方が必要になります。
例えば、\(I=[0,1]\)という集合を考えましょう。\(U_1 =(-\frac{1}{2},\frac{3}{4})\)、\(U_2 =(\frac{1}{4},\frac{3}{2})\)とすると、\(U_1,U_2\)は開集合で、\(I \subset U_1 \cup U_2\)と覆います。
\(\mathbb{R}^N\)の集合の集まり(集合族)\(\{U_\lambda\}_{\lambda \in \Lambda}\)が\(D\subset \mathbb{R}^N\)の開被覆(open covering)であるとは、すべての\(U_\lambda\)が開集合であり、\(D \subset \bigcup _{\lambda \in \Lambda} U_\lambda\)であることです。
開被覆を考えているときは、一般にその個数は有限個でなく、可算無限、非可算無限のものも想定に入れています。
\(V_k = (k,k+1.1)\)、\(k\)は整数とすると、\(\{V_k\}_{k \in \mathbb{Z}}\)は\(I\)の開被覆です。これは可算無限個でカバーしています。しかし、実際にはそのうち有限個を取り出しても\(I\)をカバーできているのです。\(V_{-1}=(-1,0.1)\)、\(V_0=(0,1.1)\)で、\(I \subset V_{-1} \cup V_{1}\)となっているので。この\(V_{-1},V_0\)を、\(\{V_k\}_{k \in \mathbb{Z}}\)の有限部分被覆(finite subcover)と呼びます。
有界な閉集合の開被覆からは、有限部分被覆が取り出せました。この有限個でカバーできるという性質を取り出したものが、コンパクトです。
部分集合\(D \subset \mathbb{R}^N\)がコンパクト(compact)であるとは、\(D\)の任意の開被覆\(\{U_\lambda\}_{\lambda \in \Lambda}\)に対し、その有限部分被覆\(U_{\lambda_1},\dots,U_{\lambda_n}\)が存在することです。
どんな開被覆を選んだとしても、その有限個でカバーできる。そういう性質を持つ、ある意味で有限的で小さくまとまった集合がコンパクトです。逆に、ある開被覆を考えると、そのどんな部分を選んでも有限個ではカバーできないとき、コンパクトではありません。
例えば、\(V_k = (k,k+1.1)\)として、\(\{V_k\}_{k \in \mathbb{Z}}\)は\(\mathbb{R}\)の開被覆でもあります。\(\bigcup _{k \in \mathbb{Z}} V_k = \mathbb{R}\)なので。しかし、どんな有限個を選んでも\(\mathbb{R}\)をカバーしきることはできません。したがって、\(\mathbb{R}\)はコンパクトではありません。
一般に、ユークリッド空間に限らず、距離を持った空間において有界な閉集合を考えることができます。距離空間においては、部分集合がコンパクトであるならば、それは有界閉集合であるという性質が成り立ちます。逆は一般には成り立ちません。
しかし、ユークリッド空間\(\mathbb{R}^N\)においては、逆も成り立つことが知られています。
ハイネ・ボレルの被覆定理(Heine–Borel theorem)
\(D \subset \mathbb{R}^N\)とする。\(D\)がコンパクトであることと、\(D\)が有界な閉集合であることは同値。
コンパクト性による証明
コンパクト性の考え方を導入すると、最大値の定理がシンプルに証明できます。ここではいくつかの一般論を事実として認め、簡単に紹介します。
\(f: I \to \mathbb{R}\)を有界な閉区間で定義された連続関数としましょう。
ハイネ・ボレルの被覆定理より、\(I\)はコンパクトです。また、一般にコンパクト集合の連続写像による像はコンパクトになることが知られています。
つまり、\(f(I)\)はコンパクトです。再びハイネ・ボレルの定理より、\(f(I)\)は有界な閉集合です。\(\mathbb{R}\)の有界な部分集合には、上限\(M\)と下限\(m\)が存在します(実数の公理)。ここで\(f(I)\)は閉集合なので、\(M \in f(I)\)です(\(M \not in f(I)\)とすると、\(M\)中心の開球を考えれば、\(f(I)\)が閉集合であることに矛盾する)。同様に、\(m\in f(I)\)です。像の定義\(f(I)=\{y \mid \exists x \in I , f(x)=y\}\)より、\(f(x_1)=m\)、\(f(x_2) =M\)となる\(x_1,x_2\)が存在します。これで最大値・最小値が存在することがわかりました。
以上、コンパクト性とは何か、有界閉集合、最大値の定理を例に紹介してきました。
コンパクト性は重要な性質ですが、その定義の抽象性、「任意の」「ある」を含んだ定義文、無限個の集合族を想定する考え方から、初めて学ぶときに苦戦する人は少なくないでしょう。まずは最大値の定理の主張、有界な閉集合について知っておくことが大事だと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (2018-11-06T00:00:00.000Z)
¥2,640
日本評論社 (2000-12-01T00:00:01Z)
¥2,420
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080
こちらもおすすめ
無限集合の濃度とは? 写像の全単射、可算無限、カントールの対角線論法