グラフ理論入門：グラフとは、グラフの同型

どうも、木村（@kimu3_slime）です。

今回は、グラフ理論の入門として、グラフとは何か、グラフの同型について紹介します。

グラフとは
グラフの同型
こちらもおすすめ

グラフとは

グラフ理論におけるグラフは、鉄道の路線図や、電気の回路、コンピュータのネットワークを表し、分析するために使われます。いわゆる「関数のグラフ」とは別物です。

例として、東京の路線図の一部、円状の山手線と、それを横断する中央線を考えましょう。

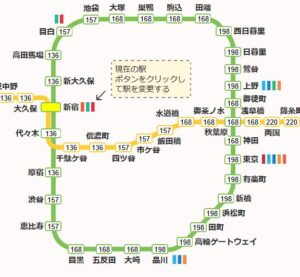
画像引用：山手線路線図 – pili.app

この駅と路線の関係性を、グラフとして抽象化すると、次のようになります。

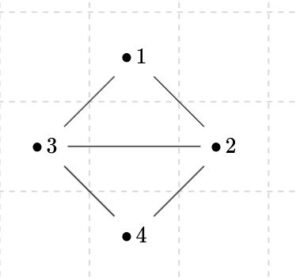
各駅は、点として抽象化されました。本来はいくつもの駅があるわけですが、駅と駅のつながり、経路の関係性を表すには、上の図の\(4\)点で足りていますね。\(3\)が新宿駅、\(2\)が秋葉原駅を表すと考えて良いでしょう。

駅と駅をつなぐ線路は、図では線として抽象化されています。ここでは直線で描いていますが、もっと曲がりくねったように書いても、現実を模したように書いても同じです。そもそも、路線図自体、地図的に正確に表したものではなく、どの駅とどの駅がつながっているかを表しているものです。グラフにおいては、点と点が「どのような曲線で」つながっているかは考えず、「どの点とどの点がつながっているか」という情報だけがあります。

では、グラフとはどういうものか、一般的に考えていきましょう。

おおざっぱに言えば、グラフ（graph）とは、頂点（vertex）と辺（edge）の集まりです。

より厳密には、集合論の言葉を使って定義されます。

頂点の集まりとは、有限集合\(V =\{1,2,\dots, N\}\)のこととします。さきほどのグラフならば、\(V=\{1,2,3,4\}\)が頂点です。グラフには、頂点と呼ばれる有限個の点の集まりがある。ここでは頂点を表す記号として数字を用いていますが、アルファベットでもなんでも良いです。

辺の集まり\(E\)も集合として考えたいわけで、ひとつひとつの辺を\(e_k\)と表すことにすれば、これも\(E=\{e_1,e_2,\dots,e_M\}\)と有限集合で表されます。辺は「\(2\)つの頂点がつながっている」ことを表すものですから、\(\{1,3\}\)といったように、\(V\)の2点からなる部分集合として定義されます。したがって、辺全体\(E\)は「\(V\)の2点からなる部分集合」のなす集合です。（集合と「集合の集合」は別物であることに注意）

そして、頂点と辺の組\((V,E)\)をグラフ\(G\)と呼ぶことにします。

この図で表されたグラフを、集合論の言葉で定式化してみます。頂点は\(V=\{1,2,3,4\}\)です。\(1\)と\(3\)をつなぐ辺は、\(\{1,3\}\)と表されます。このように考えれば、\(E=\{\{1,3\},\{1,2\},\{2,3\},\{3,4\},\{4,2\}\}\)です。例えば\(1,4\)の間に辺はありませんが、そのことは\(\{1,4\} \not \in E\)と表せます。

集合をその要素を列挙して表すとき（外延的記法）は、集合はその所属する要素のみによって決まり、要素を表す順番によって区別されていません。例えば、\(\{4,2\}=\{2,4\}\)であり、どちらで書いても同じことです。

辺に向き・矢印まで考えたグラフ、有向グラフ（directed graph）を考えるときは、辺を単なる2点の集合でなく、順序対を考えます。今回はひとまず辺の向きを考えない、無向グラフを考えましょう。

グラフ理論の主な問題は、「経路」に関する問題です。

例えば、さきほどの路線図ならば、辺に「移動時間」や「移動料金」といった重みを考えて、その上でコストが最小・最短になる経路を探せ、という問題が考えられます。これは地図アプリや乗換案内アプリで使えそうです。

歴史的には、グラフ理論は、一筆書きの可能性に関する数学者オイラーの問いによって始まったとされています。

ヨーロッパのケーニヒスベルクという土地に、次の図ような橋がかかっていました。同じ橋を二度通らずに、すべての橋を渡り切ることはできるでしょうか？　これはケーニヒスベルクの橋の問題と呼ばれています。

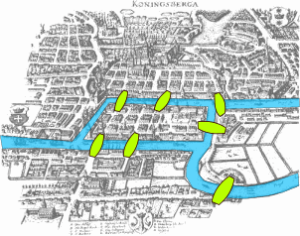
画像引用：The problem of the Seven Bridges of Königsberg. – Bogdan Giuşcă

この状況をグラフ化してみましょう。

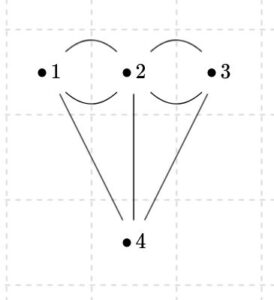
これは状況を表してはいますが、2頂点の間に2つの辺があるような状況になっています。重複する辺やループ（点それ自身への辺）を許すグラフ（非単純グラフ nonsimple graph）を考えることもできますが、今回はそれを許容しない、単純なグラフ（simple graph）を考えましょう。

ひとつの辺を\(\{1,2\}\)と表す限り、それは\(\{2,1\}\)や\(\{1,2\}\)自身とは\(E\)において区別されません。同じ\(2\)本の辺があります、とは表せないのです。それでも、頂点を増やせばきちんとつながり具合を表すことができます。

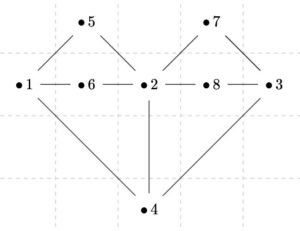
重複してしまった辺に対し、中間となる頂点を増やしてあげれば、それぞれの辺に名前（頂点）がついて区別されるわけです。

結論から言うと、このグラフは一筆書きできない（オイラーグラフでない）ことが知られています。確かに試してみると「できなさそう」ですが、なぜなのでしょうか。この話はまた別の記事にて。

グラフの同型

中学校の図形の時間では、2つの図形が平行移動、回転、反転して重なるとき、それらを合同であると呼び、区別ないものとして扱いました。

グラフでも、一見異なるように見える2つのグラフに対して、「本質的に同じグラフである」条件を考え、同一視をします。

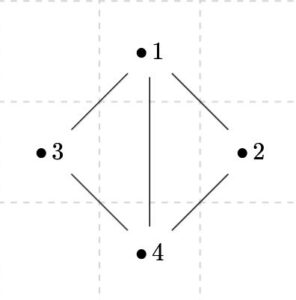
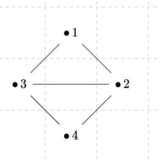
この2つのグラフは、回転させて番号をつけかえただけで、つながり具合としては同じものに見えます。

上側のグラフ\(G_1\)は、\(V(G_1)=\{1,2,3,4\}\)、\(E(G_1)=\{\{1,3\},\{1,2\},\{2,3\},\{3,4\},\{4,2\}\}\)です。下側のグラフ\(G_2\)は、\(V(G_2)=\{1,2,3,4\}\)、\(E(G_2)=\{\{1,3\},\{1,2\},\{1,4\},\{3,4\},\{4,2\}\}\)です。

「同じ」である状況を表すために、頂点同士の対応を写像\(F:V_1 \to V_2\)で表してみましょう。

\(G_1\)では\(3,2\)に辺がありますが、\(G_2\)でその役割をするのは\(1,4\)の辺です。そこで、\(F(3)=1,F(2)=4\)とします。残りは\(F(1)=2,F(4)=3\)としましょう。

すると、\(F\)は異なる頂点を異なる頂点へ（単射）、もれなく写しています（全射）。さらに、「辺である」という関係を保存しています。例えば、\(\{3,2\} \in E(G_1)\)ですが、\(\{F(3),F(2)\}=\{1,4\}\in E(G_2)\)です。他も調べると、\(\{F(1),F(3)\}=\{2,1\}\in E(G_2)\)、\(\{F(1),F(2)\}=\{2,4\}\in E(G_2)\)、\(\{F(3),F(4)\}=\{1,3\}\in E(G_2)\)、\(\{F(4),F(2)\}=\{3,4\}\in E(G_2)\)が成り立つことがわかります。

グラフが本質的に同じであることを表すのが、次の定義です。

グラフ\(G_1,G_2\)が同型である（isomorphic）とは、\(F:V(G_1)\to F(G_2)\)という全単射な写像で、辺の関係を保存するものが存在することです。すなわち、すべての\(x,y \in V(G_1)\)に対して、\(\{x,y\} \in E(G_1)\)と\(\{f(x),f(y)\}\in E(G_2)\)が同値になる。

グラフが同型であることは、\(G_1 \simeq G_2\)と記号で表すことがあります。

同型の考えを導入したことによって、グラフ理論において「点同士のつながり方だけを考える」ことの意味が明確になりましたね。

本質的でない違いを無視して同一視するという考え方は、グラフ理論だけでなく、数学に広く見られます。例えば、線形代数では線形空間（ベクトル空間）の同型を考え、それは次元が等しいかどうかで判定できます。集合論においては要素の個数（濃度）が等しいという同型を考え、群論では群の同型を考えるのです。

グラフを集合・写像の言葉を使って表すメリットは、本質的でない違いを無視して同一視することで、議論の一般性を保ったまま単純化できるから、と言えるのではないでしょうか。

以上、グラフ理論の入門として、グラフとはどういうものか、その集合論的な定義、同型について紹介してきました。

グラフ理論は集合論に馴染むための題材として良いものです。（有限集合なので比較的）簡単な例を絵を描きながら考えられますし、応用にもつながるので、ぜひ学んでみてはいかがでしょうか。

木村すらいむ（@kimu3_slime）でした。ではでは。