どうも、木村(@kimu3_slime)です。
大学受験に合格し、入学するまでの春休みに時間があるので、大学の数学を予習しておきたい。かつての高校3年生だった僕は、理学部の数学科へ進もうとして、そんなことを考えていました。
しかし、そのためにどんな大学数学の予習をしたら良いかわからず、苦戦しました。そこで、当時の自分におすすめしたい本、これから大学数学を学びたい人向けの情報を紹介します。
必要とされる大学数学の科目
まず、
- 数学専攻:数学科へ進み数学を専攻したいか
- 数学専攻以外:理学や工学、人文科学で数学を「使える」ようになりたいか
によって学ぶべき範囲や、学び方が変わってきます。
いずれにせよ大学1年次に学び、どんな分野を専攻するにせよ使う機会が多い科目が、線形代数学(せんけいだいすう)、微積分学(びせきぶん)、統計学(とうけい)です。「大学数学のロードマップ 」ではその科目を、教養数学と呼んでいます。
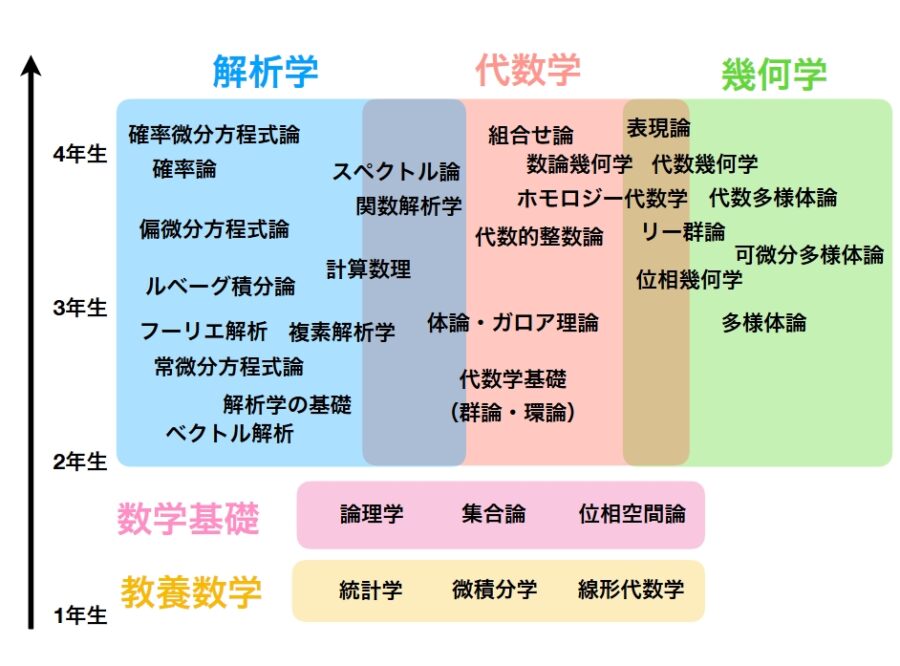
この図は数学専攻のカリキュラムを図示したもので、こんなに多くのことを学ばなくてはいけないのか、と怯えなくても良いです。どんな専門分野を後で学ぶことになったとしても、まず線形代数、微積分、統計をやっておけば、そのいずれかを使わないことはないでしょう。
やさしい本・演習書
僕はしっかりとした本を読もうとしましたが、読み解くのが難しく、しかも実践的な問題が解けるようになるわけでもなく、大学1年生の数学につまづきました。
大学数学では、高校数学で培った計算力は確かに役に立ちます。一方で、(高校ではそれほど重視されない)論理や証明が重視され、抽象的な概念が簡素に説明されがちなので、最初からきちんとした「理論」についていくのは大変です。
身の回りでも、大学1年生の授業でついていけなくて、半分あきらめてしまった、という話を聞きます。そうならないためには、「難しいことをできるようにならなくては」というプライドを捨てて、やさしく「できること」を増やすことです。
僕がたどり着いたのは、大学受験のような勉強法、まずは「(簡単な)計算問題を解けるようになること」を目指すことでした。そのために、きちんとした教科書よりむしろ、一問一答の演習書のような本を選んでいます。
より具体的には、次のマセマシリーズの本をおすすめします。本を眺めて頭をひねるだけでなく、できる問題を解く、解ける問題を増やすことです。
マセマ出版社 (2017-04-23T00:00:01Z)
¥1,980
マセマ出版社 (2020-02-05T00:00:01Z)
¥2,398
マセマ出版社 (2017-03-19T00:00:01Z)
¥2,016
マセマ出版社 (2020-02-05T00:00:01Z)
¥2,343
スバラシク実力がつくと評判の統計学キャンパス・ゼミ―大学の数学がこんなに分かる!単位なんて楽に取れる!
マセマ (2018-12-01T00:00:01Z)
¥2,500
マセマ (2017-08-01T00:00:01Z)
¥1,300
マセマシリーズは、表紙は正直胡散臭いです(笑)。「単位を取るために勉強してるんじゃない!」と当時はカッコつけて思っていました。しかし中身を読んでみると、やさしいところから書いていて、かつちゃんとした学びへの接続があるのが良いんですよね。 大学内の書店でも一番多く積まれていて、売れている本だと思います。
僕自身は、マセマシリーズは使わず、次の2冊を入門書として使っていました。
サイエンス社 (2012-07-01T00:00:01Z)
¥2,178
共立出版 (1984-12-21T00:00:01Z)
¥2,420
おそらくマセマよりは少しレベルが高い・難しいです。が、分野ごとにコンパクトな解説があり、ほかは一問一答で進む演習書という点は似たようなものです。書店で自分にあったものを選ぶのも良いでしょう。
論理のトレーニングをする本
数学を専攻しない人、理論系を専門としない人は、以上で述べた本に取り組んでいれば十分ではないかと思います。
しかし、理学部の数学科へ進む人や、1年次の講義で「イプシロンデルタ」を扱う大学では、上で紹介した演習書では足りないかもしれません。
僕の大学の1年次の数学科の授業・講義では、計算問題ではなく、むしろ理論や証明を扱うことが多かったです。僕は大学受験の数学では、まともに証明に取り組んだ記憶がなかったので、論理力を身につけるのに苦戦しました。
論理・証明・集合は、大学数学の基礎です。僕はこれらを早い段階で学ぶことが、線形代数や微積分学を深く学ぶための基礎となると思っていますが、その道・カリキュラムは整備されていないと感じています。
数学専攻の多くでは、2年次頃に「集合と位相」という科目を設けているのではないかと思います。これは論理的能力、証明のトレーニングとなる内容で、線形代数や微積分を支える科目であり、1年次から取り組む恩恵があるものです(実際、僕は集合論を先に学んでから線形代数・微積分に戻りました)。
なぜ集合(や位相)が大学数学の基礎となっているか、読み物としておすすめしたいのは次の2冊です。
ベレ出版 (2016-09-26T00:00:00.000Z)
¥1,760
「集合と位相」をなぜ学ぶのか ―数学の基礎として根づくまでの歴史
技術評論社 (2018-03-06T00:00:00.000Z)
¥2,132
現代の数学は、およそ集合論によって基礎づけられていて、(素朴には)「集合とはものの集まりである」と大学で知ったとき、「そうそう、大学数学に求めていたのはこういうのだ」と僕は思いました。
僕が大学生であった当時は、上で述べたような「なぜ学ぶのか」本は知らず、次のような解説がていねいな教科書を読んでいました。
日本評論社 (2008-12-01T00:00:01Z)
¥2,860
岩波書店 (1968-06-10T00:00:01Z)
¥1,661 (中古品)
はじめて手にとったのが、松坂「集合・位相入門」です。この本の最初の方の問題をていねいに取り組むことで、大学数学の「作法」が身につきました。「行間(書かれていない論理的なギャップ)が少ない」という意味で親切な本で、簡単かというと微妙なラインですが、僕にとってはバイブルです。
集合の基礎は論理にあるものの、数学科の講義ではあまり論理に明示的に言及してくれません。その話題がまとまっていて、かつ解説が詳しいのが嘉田「論理と集合から始める数学の基礎」でした。命題とは何か、論理と集合がパラレルに扱われることについて、きちんと書かれているのが良いと思います。
集合論は数学の基礎、論理を学ぶ題材として良いものの、少し抽象的な部分があります。まずは、数の性質(初等整数論)を通して、簡単な証明を実際にできるようになることの方が、抽象的な集合論に手を出す前の段階として良いと思っています。
学生時代はそういう本を知らなかったのですが、次の2冊が、初等整数論を証明を学ぶ題材として扱っていて、論理や集合論と結びつくものとして良いでしょう。
ゲアリー・チャートランド(著), アルバート・D・ポリメニ(著), ピン・チャン(著)
丸善出版 (2014-02-28T00:00:01Z)
¥3,850
Richard Hammack (2019-07-19T00:00:01Z)
¥3,376
特に「Book of Proof」は、ウェブ上でPDFが公式に無料で公開されています。内容も「証明の楽しみ」より若干やさしいです。なので、高校を卒業して大学数学に興味がある、という高校生(当時の僕)がいたら、Book of Proofを最初の一冊としておすすめしたいです。
残念なのが現状は英語版しかないということですが、数学の英語は他の分野に比べてやさしいので、大学受験に合格するくらいの英語力があれば余裕で読めます。数学を専攻する人はいずれ、洋書や英語の論文を読むことになりますし、洋書には世界的に評価が高い良い教科書が多いです。英語の数学の本を読む1冊目としても、ぜひトライしてみてください。
格調の高い本格的な本
大学の数学を学びたい人は、どうせ時間があるならば、基礎からしっかりとごまかしなく学びたい、という人も少なくないのではないでしょうか。
僕は高校の先生に「大学数学の予習で何を学ぶと良いか」と聞いて、確かイプシロンデルタの話をされ、それがのっている本として、
宮島「微分積分学」を買いました。そして挫折しました(笑)。
参考:大学数学の教科書の読み方、最初に「定義・命題・証明」を知ろう
最初は「実数とはどういうものか(実数論)」から始まるのですが、定義や証明が何をしているのかわからず、なぜこんな基礎を長々と話しているのかも、当時はよくわかりませんでした。(それは、上で述べた論理のトレーニングができる本を読んでからは、わかるようになりました。)
理学部数学科で数学を専攻する人の間では、次の東京大学出版会の本が有名ではないでしょうか。
東京大学出版会 (1966-03-31T00:00:01Z)
¥2,090
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740
これらは実際に僕が使った教科書で、大学院入試に向けた勉強でもお世話になりました。難しめの演習問題や話題も、だいたいこの本にはのってます。いわば辞書的に使えます。定義もしっかりしていますし、基礎的な定理の証明も全部のっています。
しかし濃度は高く、挫折する可能性は高いのではないでしょうか(笑)。1ページ読むのにも時間がかかるタイプの本です。1から全部読むのではなく、やさしい本で書かれていた内容を、詳しく知りたくなったときに参照する本として使えます。
いわばこれらは格調の高い、本格的な数学書です。もう少し前の世代だと、次の2冊が有名でしょう。
裳華房 (2015-06-05T00:00:01Z)
¥3,740
岩波書店 (2010-09-16T00:00:01Z)
¥3,520
佐竹「線型代数学」や高木「解析概論」は、扱う話題は難しいものの数学の深い理解を促す題材が多い味のある本で、名著と名高いです。しかし、難しくて読めなくては宝の持ち腐れなのではないか、とも思っています。
きちんと読めないなら、もっとやさしい本から読むのが現実的。東京大学出版会の本は、きちんとしている本であるものの、ちょっと難しすぎかな、と思っています。高校卒業レベルで読めて、かつ本格的な数学書への接続としておすすめしたいのが次の本です。
世界標準MIT教科書 ストラング:線形代数イントロダクション
近代科学社 (2015-12-22T00:00:01Z)
¥8,800
岩波書店 (1978-03-23T00:00:01Z)
¥5,170
岩波書店 (1981-11-15T00:00:01Z)
¥5,720
どれも洋書を翻訳したもので、英語圏の教科書として定番です。おそらく大学1年生で前提とする知識が日本に比べて少ないので、高校レベルの内容の復習から入っているのがとても良いと思います。大学1年生の頃は教科書が難しくて読めずに苦しんでいましたが、最初にこの本に出会いたかった……(笑)という本です。
以上、大学入学前に数学を予習したい人向けにおすすめの本として、簡単な演習書、論理トレーニングになる本、本格的な本を紹介してきました。
そもそも、高校を卒業した時点では、書店に行っても自分にどんな本が必要なのか、ってわからないんですよね(僕にはわかりませんでした)。
線形代数、微積分、統計学といった教養数学があり、それらを支える集合や論理といった分野があります。それをやさしいところから読める本は、紹介した通りです。
学問に王道なし、千里の道も一歩から、です。欲張りすぎずに、面白そうな本から、ノートを書きながら読んでみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
大学数学の教科書(数学書)が難しいのはなぜ? 読み方を考える