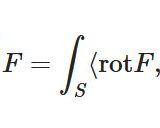どうも、木村(@kimu3_slime)です。
ベクトル解析における名のついた有名定理といえば、グリーンの定理、ストークスの定理、ガウスの発散定理です。
今回は、ガウスの発散定理とは何か、その計算例、電磁気学への応用を紹介します。
ガウスの発散定理とは
ガウスの発散定理は、3次元空間\(\mathbb{R}^3\)におけるベクトル場に関する定理で、あある領域での重積分とその境界での面積分を関係付けるものです。
まずは、一般的な主張を見てみましょう。
発散定理(divergence theorem)
\(D\subset \mathbb{R}^3\)を有界な領域、\(S\)をその境界とし、それはいくつかの\(C^1\)級の関数でパラメータ表示されるとする。\(F:\mathbb{R}^3 \to \mathbb{R}^3\)を\(C^1\)級のベクトル場、\(F=(F_1,F_2,F_3)\)とする。このとき、次の等式が成り立つ。
\[ \begin{aligned}\int_S \langle F,n\rangle = \int_D (\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z}) dxdydz\end{aligned} \]
右辺の重積分の被積分関数は、ベクトル場\(F\)の発散(divergence)と呼ばれるものです。
\[ \begin{aligned}\mathrm{div }F:=\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z}\end{aligned} \]
ベクトル場の発散は、流入と流出、湧き出しと沈み込みの量を捉えるものであり、その\(D\)における合計を求めるのが右辺の重積分です。発散に関する定理だから、発展定理と呼ばれるわけですね。
具体例で確かめる
ガウスの発散定理は、どういうことを言っているのでしょうか。具体例を通じて確かめてみます。
\(F(x,y,z)=(-x,-y,-z)\)というベクトル場について考えます。これは次のように図示されるものです。
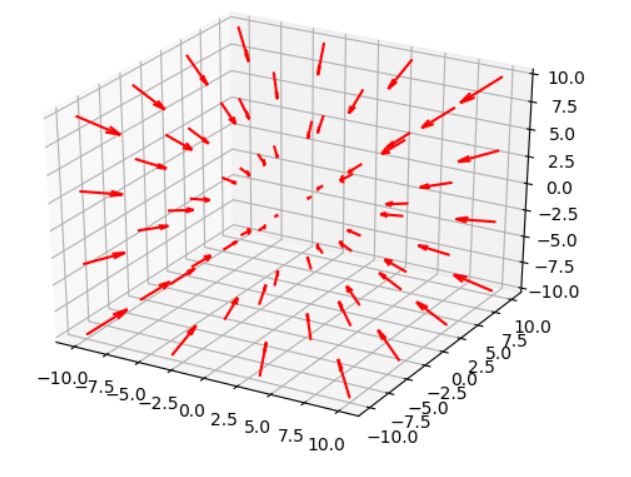
\(F\)の発散は\(\mathrm{div}F=-3\)とマイナスであり、常に原点側への流入が起こっていることがわかりますね。
考える領域としては、半径\(r\)の球体の内部\(D= \{(x,y,z)\mid x^2+y^2+z^2 \leq r^2\}\)としましょう。その境界となる曲面は、球面\(S=\{(x,y,z)\mid x^2+y^2+z^2 = r^2\}\)です。
まず、面積分\(\int_S \langle F,n\rangle\)を求めます。
球面のパラメータ表示\(p(\theta,\phi)\)について、その法線ベクトルは\(p_{\theta} \times p_{\phi} =r \sin \theta \,p(\theta,\phi)\)です。したがって、それとベクトル場の内積は\(\langle F,p_{\theta} \times p_{\phi} \rangle=r \sin \theta \langle -p(\theta,\phi),p(\theta,\phi)\rangle= -r^3 \sin \theta\)となります。よって、面積分は
\[ \begin{aligned} \int _S \langle F,n\rangle&= \int _0 ^{2\pi } \int_0 ^{\pi}\langle F(p(\theta,\phi)),p_\theta \times p_\phi \rangle d\theta d\phi \\ &= \int _0 ^{2\pi } \int_0 ^{\pi} -r^3 \sin\theta d\theta d\phi \\&=2\pi r^3 [\cos \theta]_0^\pi \\ &=- 4 \pi r^3 \end{aligned} \]
となります。
続いて、重積分\(\int_D \mathrm{div}F dxdydz\)を求めます。
\(\mathrm{div}F=\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z}=-3\)です。\(D\)の体積は\(\frac{4}{3}\pi r^3\)であり、
\[ \begin{aligned}\int_D \mathrm{div}F dxdydz\ = -3\int_D dxdydz= -4\pi r^3\end{aligned} \]
と結果が一致することがわかりました。このケースでは確かに発散定理が成り立っています。
今回は、後者の方が計算が簡単でした。前者の面積分を求めなさいという問題は、発散定理を用いれば、発散の重積分を求めなさい、という問題に変換できます。(逆もしかり)
特殊ケースでの証明
発散定理が成り立つ理由を、特殊なケースで調べてみましょう。\(F=(F_1,F_2,F_3)\)を一般のベクトル場とし、\(D=[0,1]\times[0,1]\times[0,1]\)という立方体を考えます。
\(S_1 =\{(0,y,z)\mid (y,z) \in [0,1]\times[0,1]\}\) 、\(S_2 =\{(1,y,z)\mid (y,z) \in [0,1]\times[0,1]\}\)という2つの面に注目しましょう。それぞれの外向きの単位法線ベクトルは、\(n_1 =(-1,0,0)\)、\(n_2 =(1,0,0)\)です。したがって、
\[ \begin{aligned}\int_{S_1} \langle F,n_1\rangle = \int \int -F_1(0,y,z)dydz\end{aligned} \]
\[ \begin{aligned}\int_{S_2} \langle F,n_2\rangle = \int \int F_1(1,y,z)dydz\end{aligned} \]
となります。一方で、微積分学の基本定理より、
\[ \begin{aligned} \int _D \frac{\partial F_1}{ \partial x} dxdydz &= \int \int [F_1]_{x=0}^{x=1}dydz \\ &= \int \int F_1(1,y,z)dydz -\int \int F_1(0,y,z)dydz \ \end{aligned} \]
となり、境界での面積分の和と一致しています。これは\(y,z\)方向にも同様に成り立つので、
\[ \begin{aligned}\int_S \langle F,n\rangle = \int_D (\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z}) dxdydz\end{aligned} \]
が成り立つことが言えました。
\(D\)が立方体でなく一般の領域であっても、基本的にはこの計算に帰着させることで証明できます。これはグリーンの定理の証明と同様ですね。証明について詳しくは、杉浦「解析入門 Ⅱ」の8章を参照してください。
電磁気学への応用
発散定理は、ガウスの名を冠するように、電磁気学におけるガウスの法則への応用を持ちます。
\(E:\mathbb{R}^3 \to \mathbb{R}^3\)を電場(ベクトル場)、\(\rho:\mathbb{R}^3 \to \mathbb{R}\)を電荷密度、\(\varepsilon_0>0\)を真空の誘電率として、
\[ \begin{aligned}\mathrm{div}E =\frac{1}{\varepsilon_0} \rho \end{aligned} \]
が成り立つというのがガウスの法則です(静電場、静磁場の仮定における式)。
有界な領域\(D\subset \mathbb{R}^3\)で、なめらかな境界\(S\)を持つものを考え、そこで両辺を重積分してみます。
\[ \begin{aligned}\int _D \mathrm{div}E =\frac{1}{\varepsilon_0} \int _D \rho \end{aligned} \]
左辺は、ガウスの発散定理より、\(n\)を\(S\)の外向き単位法線ベクトルとして、
\[ \begin{aligned}\int _D \mathrm{div}E =\int _S \langle E,n\rangle \end{aligned} \]
と表せます。電荷の総量を\(Q:= \int _D \rho\)と置けば、
\[ \begin{aligned}\int _S \langle E,n\rangle =\frac{1}{\varepsilon_0} Q\end{aligned} \]
となります。左辺は電場\(E\)が境界\(S\)を通り抜ける量(電気力線という)であり、右辺は内部の電荷の合計で、それらが等しいというのがガウスの法則の主張というわけです。
出発点とした式はガウスの法則の微分形、変形によって得た式はガウスの法則の積分形と呼ばれます。発散定理は、微分形と積分形、ミクロとマクロの見方を結びつけています。
似た形の法則として、磁束保存の法則があります。\(B\)を磁界として、
\[ \begin{aligned}\mathrm{div} B =0\end{aligned} \]
というものです。発散定理より、これは
\[ \begin{aligned}\int _S \langle B,n\rangle =0\end{aligned} \]
とも言いかえられます。これは磁石においては正負の力が常に両方バランス取るようにしか存在せず、N極やS極しか持たない磁気単極子(モノポール)が存在しないことを主張するものです。
ガウスの法則や磁束保存の法則、(ファラデーの法則、アンペールの法則)は、電磁気学においてマクスウェル方程式という4つの方程式にまとめられています。ガウスの発散定理(やストークスの定理)は、電磁気学を理解するために基本的なものです。
今回は、ガウスの発散定理とは何か、その計算例、簡単なケースでの証明、電磁気学への応用を紹介しました。
内部と境界を結びつけるという点では、微積分学の基本定理のようなもので便利なので、ぜひこの視点の行き来をマスターしてみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1981-11-15T00:00:01Z)
¥5,720
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740