なぜ中学・高校数学を学ぶのか数理モデルとしての微分方程式

どうも、木村（@kimu3_slime）です。

今回は、微分方程式（びぶんほうていしき）という数学の考え方が、中学・高校数学、理科を学ぶ理由のひとつとなるくらい大事なものである、という話をします。

数理モデルとしての微分方程式
微分方程式を目標とした学び方
こちらもおすすめ

数理モデルとしての微分方程式

まず、科学や数学の歴史を、数百年ほど振り返りましょう。科学技術は、（良くも悪くも）僕たち人間の生活を大きく変化させてきました。

最近で言えば、コンピュータ、インターネット、スマートフォンといった情報技術の普及は目覚ましいです。戦後の日本であれば、テレビ、冷蔵庫、洗濯機といった家電は三種の神器と呼ばれるほどですが、それは電気（と磁気）が制御できるようになったおかげで生まれたものです。さらに遡れば、鉄道や工場、車の誕生といった産業革命がありましたが、それは燃料を力に変換する技術、熱力学に支えられています。それ以前のヨーロッパでは、天体の運動と地上の運動に共通の法則があるといった科学革命がありましたが、それは力学・物理学の発展によるものです。

こうした近世や近代において社会を大きく変化させてきた科学技術には、数学が共通して関わっています。

「それでも地球は動いている」と地動説を主張したガリレオ・ガリレイは、「宇宙という書物は数学の言葉で書かれている」という言葉を残しています。宇宙や自然現象がどういうものなのか捉えるにあたって、数学は言語のような役割を果たしている、と言っているわけです。

で、その言語といっても色々あるわけですが、そのうち重要なものに微分方程式があります。

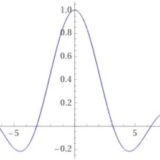
微分とは瞬間的でミクロな変化を捉えるものですが、一瞬一瞬の変化の法則を定めることで、多くの長期的な現象を説明できます。

2020年以降、コロナウイルス感染症が世界的に流行していますが、その増減を予想するような感染症モデルが知られています。

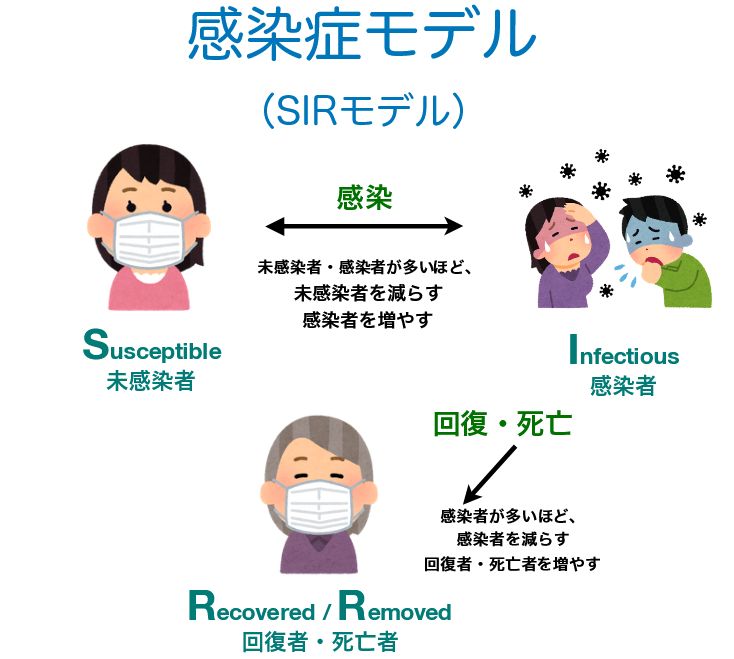
参考：数学とコロナ～感染症の数理モデルをやさしく解説 – Share Studies

（数理）モデルとは、複雑な現実を単純に表しつつも、現象の本質を再現しようとしている数式のことです。感染症モデル（SIRモデル）は、微分方程式によってモデルが表されています。

力学であれば運動方程式、音や光であれば波動方程式、電磁気であればマクスウェルの方程式といった微分方程式を使ったモデルが主流です。自然現象を説明する基本的なモデル全般は、基礎方程式とも呼ばれます。

熱が伝わって広がったり、花粉が飛ぶ現象には熱伝導方程式、拡散と呼ばれる微分方程式が登場します。

参考：なぜ偏微分を学ぶ？フーリエの熱伝導方程式を例に、花粉の広がりを数式で予測する、拡散方程式とは

シマウマやキリンなど動物の縞模様も、反応拡散方程式と呼ばれるモデルで説明できるといった例もあります。

参考：生き物の模様は数式で決まる？チューリング・パターンとは

これらの微分方程式は、最初から知られていたわけではなく、多くの実験や観測を繰り返す中で、人々が見出してきたものです。

現象を観測し、それを理科的な知識と合わせて微分方程式としてモデル化する。そのモデルを解いて、現実に観測されるデータとマッチした良いモデルになっているか確かめた上で、多くの現象に活用していく。こうした流れは、数理モデルを利用する多くの学問に共通したものです。

複雑な現象を、できるだけシンプルな数式（＝モデル）に落とし込み、分析する。その数式として広く利用されてきたのが微分方程式であり、だからこそ多くの人が簡単にでも読み書きできるようになっておくと良いな、と思っています。

微分方程式を目標とした学び方

（簡単な）微分方程式は、中学・高校数学、理科の目標のひとつとする価値のある重要な対象だと思っています。

なぜ中学や高校で数学を学ばなければならないのか、どんな意義があるのか、学校でまともな回答を聞いた覚えが僕にはありません。その理由のひとつは、多くの現象を記述するときに利用される数学的な言語、微分方程式を理解するためだよ、と言ってくれたらはっきりとします。（他にもいくらでも理由は挙げられますが、何にせよ具体的にひとつ提示してほしいものですね）

参考：中学・高校数学のロードマップ～分野一覧と学ぶ順序

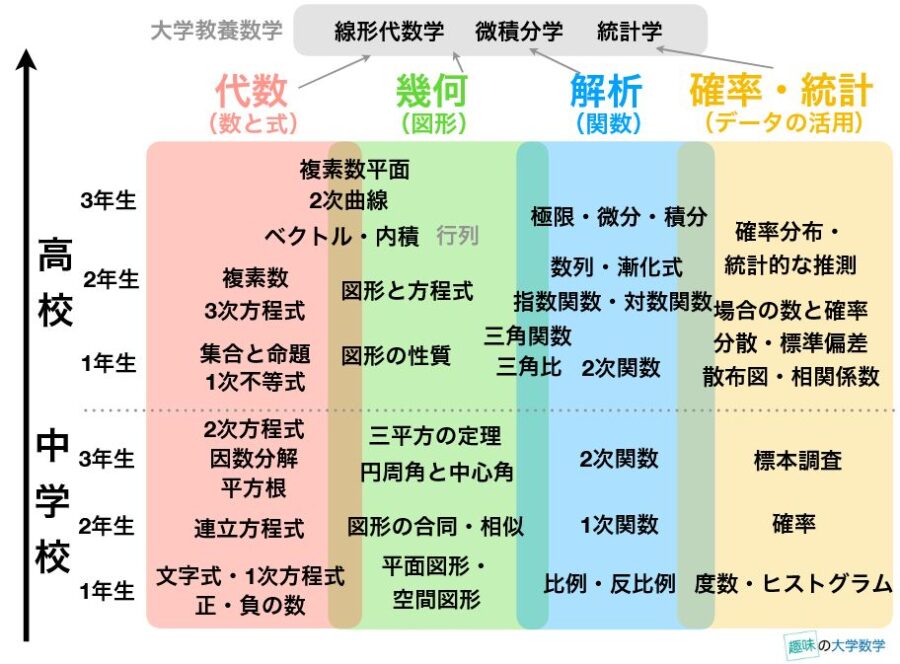
中学、高校の数学を、微分方程式の理解という目標から整理してみましょう。

「微分」という言葉が登場するように、高校数学の数学II、数学IIIで登場する微分と積分の理解が重要です。それがわかれば、微分方程式の一歩手前です。数列や漸化式は、微分方程式と似ている話題で、数理モデルの話とも言えます。

微分方程式の「解」は、何らかの関数となります。一定の速さを保った運動なら1次関数、加速していく運動なら2次関数、ばねのような周期的な運動なら三角関数、生物の爆発的な増加なら指数関数といったように、関数を知ることで理解できる現象の幅が広がるのです。また、三角関数の理解には、三角形の相似や三平方の定理といった、図形・幾何の知識が必要となります。

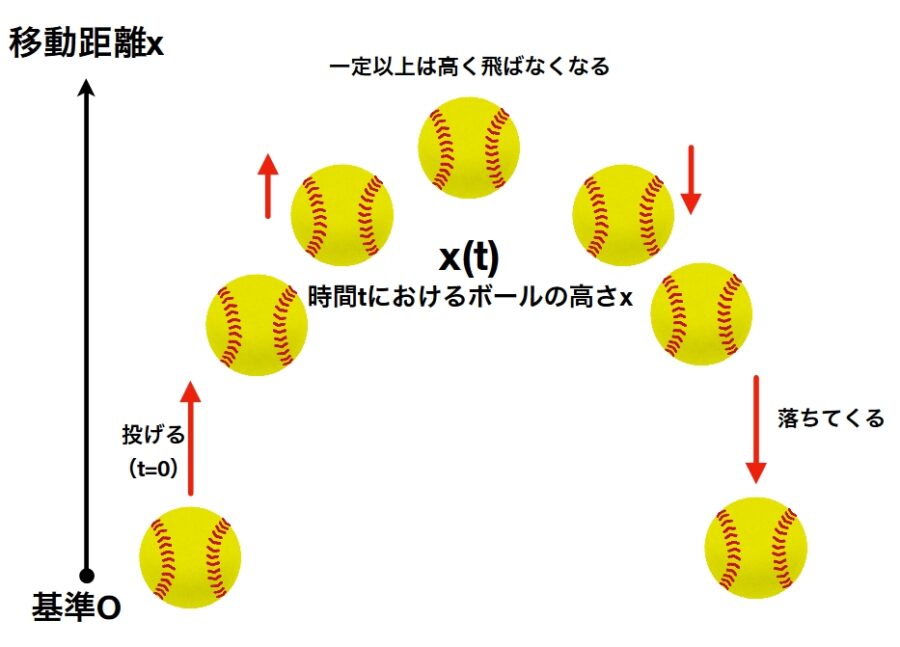
関数を考えるときは、\(x(t)=-(t-2)^2 +4\)といったように、位置など変化する量\(x\)を、時間といった変数\(t\)によって表します。変化する現象全体を記述するためには、数を記号・文字式で表す必要があるのです。2次方程式や因数分解は、関数のグラフの概形を理解するのに役立ちます。

高い場所からものを投げると、時間が経てば今自分のいる場所より低い場所へ落ちていくことがあります。そういう現象には、数直線や負の数といった考え方を利用した方が便利です。また、物体の運動を例にすれば、時間は1,2,3秒と途切れていると考えるのは不自然です。現実の運動は、細切れの漫画ではなく、連続的に見えます。したがって、小数や分数だけでなく、無理数を含む数（実数）を扱う必要がでてきます。

以上、数理モデルとしての微分方程式の重要性、中学・高校数学との関係を述べてきました。

その重要性にもかかわらず、現行の中学・高校・大学のカリキュラムにおいて、ごく簡単な数理モデルとしての微分方程式に触れる機会は少ないです。もし数学や理科を学ぶ意義を疑問に思ったら、現実と数式の関わり合い、微分方程式の話を思い出してみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。