平方完成の由来と応用：なぜ平方「完成」と呼ばれるか

どうも、木村（@kimu3_slime）です。

今回は、高校数学で学ぶ平方完成という用語の由来と応用について、図を交えつつ紹介したいと思います。

平方完成とは何か

平方完成とは、2次の多項式\(ax^2+bx+c\)を扱いやすい形\(a(x+d)^2+e\)に変形することです。

具体的に見てみましょう。\(x^2-2x+5\)を平方完成してみます。

\[ \begin{aligned} x^2-2x+5 &=( x^2 -2x +1 )-1+5 \\ &= (x-1)^2+4\end{aligned} \]

となります。1次の多項式の平方＝2乗\((x-1)^2\)をくくりだすのがポイントです。

\(y=x^2-2x+5\)で表される2次関数は、平方完成することによって、頂点が\((x,y)=(1,4)\)であることがわかりやすくなります。

また、\(x^2-2x+5=0\)により定まる2次方程式は、\((x-1)^2=-4\)なので、\(x\)が実数の範囲では解を持たないことがわかります。（複素数の範囲まで考えれば、\(x-1 = \pm 2i\)で、\(x=1+\pm 2i\)と求めやすいですね。）

では、平方完成の由来は何なのでしょうか。

英語では、”Completing the Square“と呼ばれます。squareは正方形、2乗を意味する英語で、completeは完成させること。略せば平方完成ですが、正方形の完成といった方が日本語的にはイメージしやすいでしょう。

2次の多項式\(x^2-2x+5\)を図形の面積と見て、たしかに正方形を作り出していることを見てみましょう。

\(x^2\)は一辺が\(x\)の正方形、\(-2x\)と\(5\)は長方形です。これらを足し合わせたものを変形することで、正方形を作り出します。

まず\(2x\)を\(x^2\)から引くと、長方形\(x(x-2)\)ができあがります。これは正方形ではありません。そこで、その長さ\(x,x-2\)の平均\(\frac{x+(x-2)}{2}=x-1\)を基準に正方形を作れないか考えます。

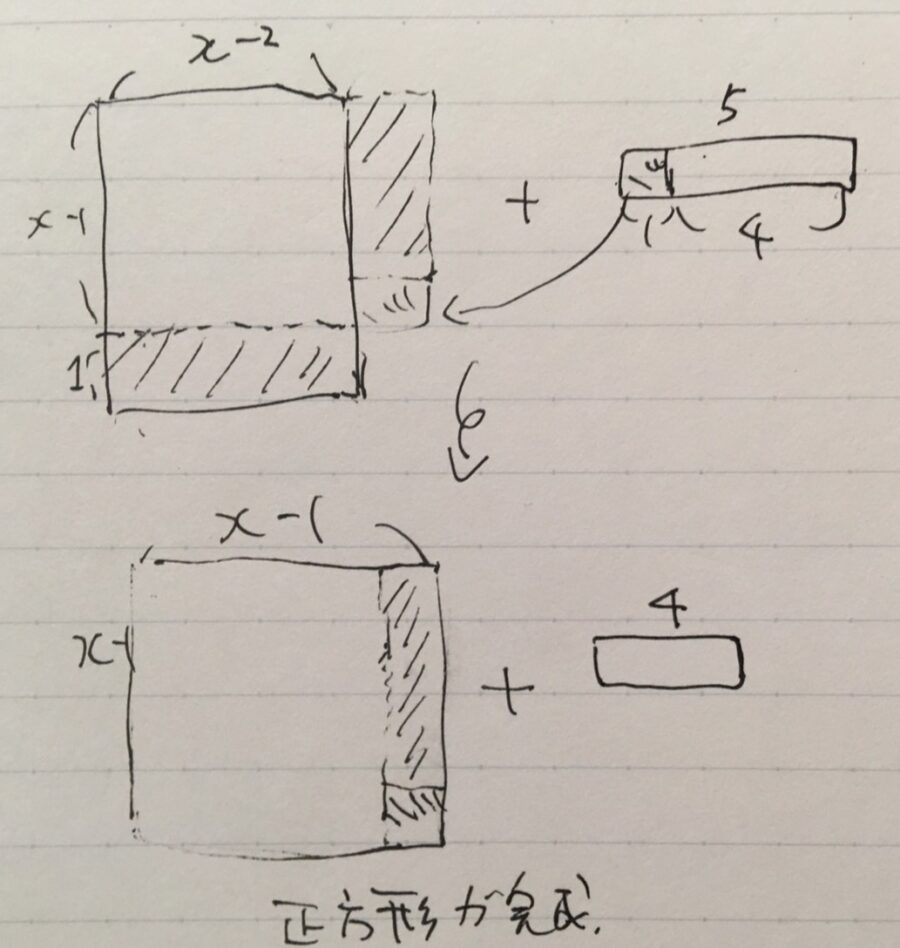
長方形\(x(x-2)\)の一辺\(x\)を1だけ削って、\(x-2\)を\(x-1\)に合わせようとしてみましょう。\(x(x-2)=(x-1)^2 -1 \)となり、正方形に\(1\)足りない状態となっています。

そこに残っていた\(5\)から\(1\)わけることで、\(x^2-2x+5=(x-1)^2+4\)と、\(x-1\)の正方形が完成します。これが平方完成というわけです。

一般の2次多項式\(ax^2 +bx+c\)の平方完成も、同じアイデアです。（\(a\neq 0\)とする）

\(ax^2\)という正方形と、\(bx,c\)という長方形があると考えます。前者2つをまとめて、新たに正方形を作れないか、という考え方をするわけです。

まず、\(ax^2\)を基準とするように、面積全体を\(\frac{1}{a}\)倍しましょう。すると、\(a(x^2+\frac{b}{a}x +\frac{c}{a} )\)です。

前半2つの項からできる長方形\(x^2+\frac{b}{a}x=x(x+\frac{b}{a})\)を正方形にしたいです。2つの辺の長さを平均すれば、\(\frac{x+(x+\frac{b}{a})}{2}=x+\frac{b}{2a}\)という長さが見つかります。

単純に正方形を考えると、\((x+\frac{b}{2a})^2=x^2 +\frac{b}{a} x+\frac{b^2}{4a^2}\)と「余り」が出てきてしまいます。これは\(\frac{c}{a} \)と調整すれば良いのです。よって、

\[ \begin{aligned} ax^2 +bx+c&= a(x^2+\frac{b}{a}x +\frac{c}{a} )\\ &=a((x+\frac{b}{2a})^2-\frac{b^2}{4a^2}+\frac{c}{a}) \\ &= a(x+\frac{b}{2a})^2 -\frac{b^2-4ac}{4a} \end{aligned} \]

と平方完成できました。一辺が\(x+\frac{b}{2a}\)の正方形を、\(x\)の関わらない部分と調整して作りだしているわけですね。

この一般的な平方完成は、解の公式を導くものです。

\( ax^2 +bx+c=0\)という方程式は、平方完成によって\(a(x+\frac{b}{2a})^2 -\frac{b^2-4ac}{4a} =0\)と同値です。

したがって、\((x+\frac{b}{2a})^2=\frac{b^2-4ac}{4a^2} \)で、両辺の平方根を取れば\(x+\frac{b}{2a} = \pm\frac{\sqrt{b^2-4ac}}{2a} \)となります。移行すれば、\(x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}\)と解の公式が得られました。

これは、一辺の長さが\(x+\frac{b}{2a}\)の正方形と、一辺が\(\sqrt{\frac{b^2-4ac}{4a^2}}\)である正方形の面積を比較して、両者が等しくなるような長さ\(x\)を探した、と捉えることができます。

辺の長さに\(x\)を含む長方形の面積であっても、正方形に直してしまえば（平方完成すれば）、面積と辺の長さの関係が明白になるのです。

以上、平方完成の由来と応用を紹介してきました。

2次多項式の計算にあたっては、今回紹介したような幾何学的なイメージは、必ずしも必要ありません。イメージにとらわれず、記号をルールに従って操作できることが大事です。

ただ、もし平方完成という用語に疑問を覚えたら、2乗＝平方＝正方形を作っているのだということを、思い出してみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。