積分とは何か？面積を長方形で近似計算してみよう

どうも、木村（@kimu3_slime）です。

今回は、積分とは何か、グラフの面積を長方形で近似計算しつつ、その定義や計算方法について紹介します。

積分＝微分の逆？
面積を長方形で近似する
区分求積法と積分の定義
こちらもおすすめ

積分＝微分の逆？

積分とは何でしょうか。高校レベルの数学の教科書では、\(f\)の（不定）積分とは、微分して\(f\)になるような関数\(F\)のことであると定義されるのが一般的です。

\[ \begin{aligned}\int f(x)dx =F(x) :\Leftrightarrow F'(x) =f(x)\end{aligned} \]

このような関数\(F\)は、\(f\)の原始関数と呼ばれました。つまり、積分＝微分の逆を計算すれば良い、といった定義です。

このような定義にもかかわらず、定積分によって\(f\)のグラフの面積が求められることになっています。グラフの高さ（線分）を足し合わせたものが積分とも説明されますが、先ほどの定義と整合性がありません。どうして微分の逆をすると面積が求まるのでしょうか。

本来的には、関数\(f\)の積分は、そのグラフの面積として定義されるのです。原始関数を求めることで面積計算ができることは、奇跡的な発見で、それは微積分学の基本定理と呼ばれています。高校における積分の定義は、結果を先取りしたショートカットをしているわけです。

今回は、積分＝面積と定義した上で、それを近似計算してみましょう。

面積を長方形で近似する

面積とは、そもそも何でしょうか。

根源的な定義は、長方形の面積です。それは縦かける横、底辺かける高さによって求められる量と約束します。

ただし、一般的な図形やグラフの面積は、長方形ではありません。しかしながら、曲がった図形を細かい長方形で近似していくことはできるのです。それこそが積分の発想。

やってみましょう。\(f(x)=\sin x\)の\(0\leq x \leq \pi\)における面積を\(S\)として、それを近似する長方形をいくつか考えてみます。

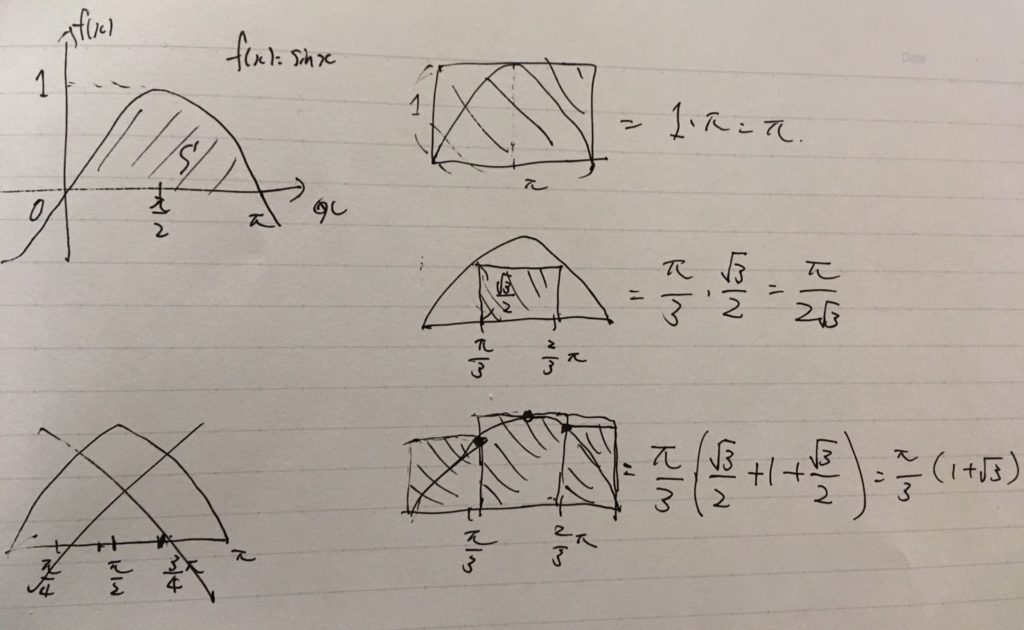
素朴に、グラフすべてを一様におおうような長方形を考えれば、その面積は\(\pi\)です。つまり、この長方形よりグラフの面積は小さいわけですから、\(S\leq \pi\)がわかります。

グラフの内側に長方形を作ってみます。区間\(0\leq x \leq \pi\)を均等に3分割すれば、内接する長方形の面積は\(\frac{\sqrt{3}\pi}{6}\)です。したがって、\(\frac{\sqrt{3}\pi}{6}\leq S\)がわかります。

結果を合わせると、\(\frac{\sqrt{3}\pi}{6}\leq S \leq \pi\)です。小数で近似すれば、グラフの面積は\(0.5\)以上\(3.2\)以下であることがわかります。

もっと細かな長方形を考えてみましょう。

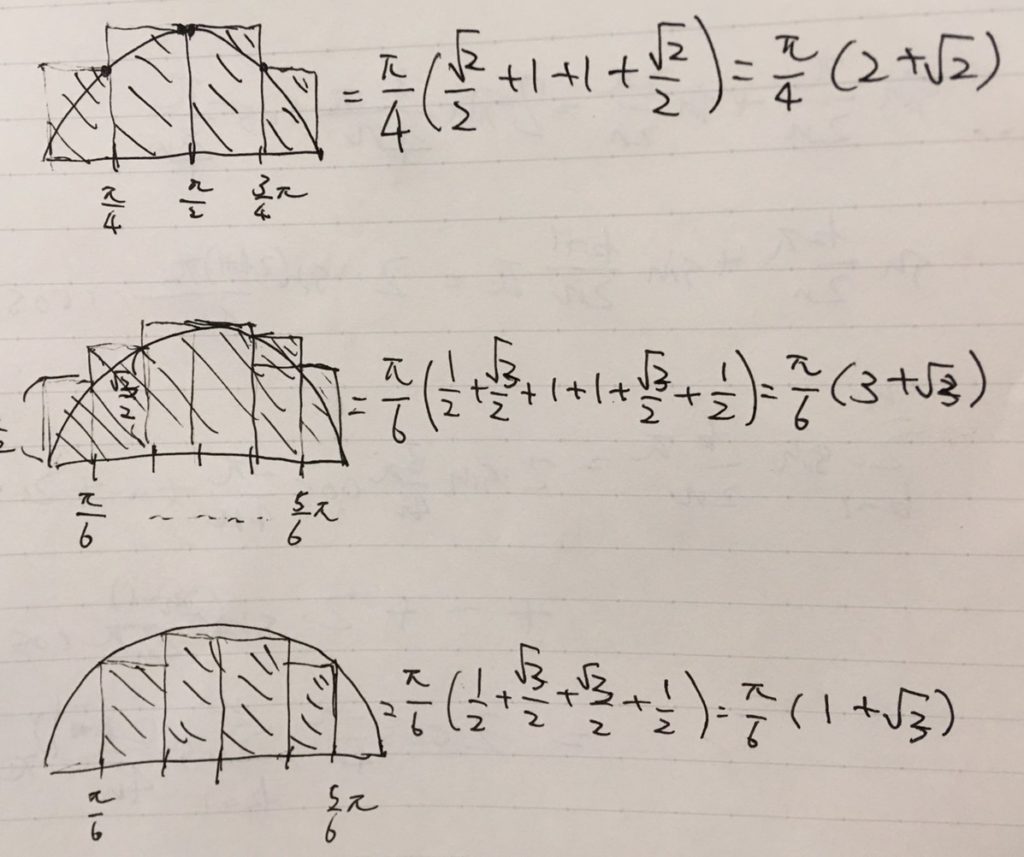
\(6\)分割までは、簡単にその値が求められます。上の画像で示した計算により、\(\frac{\pi}{6}(1+\sqrt{3})\leq S \leq \frac{\pi}{6} (3+\sqrt{3})\)です。少なくとも、\(1.5\leq S \leq 2.9\)がわかります。分割を細かくすることで、精度が良くなってきました。

この計算では、グラフを大きく外側から長方形で囲んだ面積と、小さく内側から長方形で囲んだ面積を求めています。これらは\(f\)の上限和（upper sum）、下限和（lower sum）と呼ばれる量です。

区間\(0\leq x \leq \pi\)を等分割して小さな区間に分けているわけですが、上限和ならば小区間における\(f\)の最大値、下限和ならば最小値によって計算しています。

\(2,3,4,6\)と分割を細かくしていくにつれ、上限和と下限和はそれぞれある一定の同じ値に近づいていきそうです。その極限値を、\(f\)の積分と定義するわけです。

実際に上限和や下限和の極限を求めるのは、できなくはありませんが、やや大変です。近似する長方形の作り方を、少し工夫してみましょう。

区間\(0\leq x \leq \pi\)を\(n\)等分します。そして、小区間\(\frac{k-1}{n}\pi\leq x\leq \frac{k}{n}\pi\)における\(f\)の値を、\(f(c_k)=\sin c_k\)と代表させることにします。すると、長方形を足し合わせた有限和（リーマン和と呼ばれる）は

\[ \begin{aligned}\frac{1}{n} \sum _{k=1}^{n}\sin c_k \end{aligned} \]

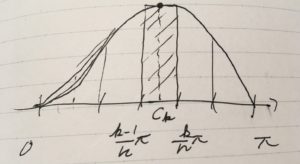
です。この和を求めるために、代表点\(c_k\)の選び方を工夫します。

平均値の定理

区間\(a\leq b\)において\(g\)が微分可能ならば、\(g(b)-g(a)= g^{\prime} (c) (b-a)\)を満たす\(c\quad (a\leq c\leq b)\)が存在する

平均的な変化率は導関数によって表されるという定理ですが、右辺を基準に逆に捉えましょう。つまり\(g'(x)= \sin x\)とする、すなわち\(g=-\cos x\)とすることで、右辺を左辺によって言い換えることができる。つまり、\(\sin c_k\)を端点における\(\cos\)の差として表せます。

平均値の定理を、\(g=-\cos x\)として、区間\(\frac{k-1}{n}\pi\leq x\leq \frac{k}{n}\pi\)に適用すると、\(-\cos(\frac{k}{n}\pi)+\cos(\frac{k-1}{n}\pi)= \frac{1}{n}\sin (c_k) \)を満たす\(c_k\)が存在します。したがって、

\[ \begin{aligned} \frac{1}{n} \sum _{k=1}^{n}\sin c_k &= \sum _{k=1}^{n} (-\cos(\frac{k}{n}\pi)+\cos(\frac{k-1}{n}\pi)) \\ &= \cos 0 -\cos \pi \\ &= 2\end{aligned} \]

となります。途中の和は、端点の値が同じなのでキャンセルして消えて、結局\(x=0,\pi\)の値だけが残ります。右辺は\(n\)によらないので、区間を細かくしたときの長方形の面積の極限値は

\[ \begin{aligned} \int \sin x dx &:= \lim_{n\to\infty} \frac{1}{n} \sum _{k=1}^{n}\sin c_k\\ &= 2\end{aligned} \]

と求められました。

これは高校流の積分計算

\[ \begin{aligned}\int _0^\pi \sin x dx =[-\cos x ]_0^\pi =2 \end{aligned} \]

と全く同じです。長方形による面積近似の極限が、原始関数によって計算できることが、少しは納得できたでしょうか。

区分求積法と積分の定義

グラフを短冊のように細かな長方形に分割して、その極限を求める……その計算は、区分求積法と呼ばれています。

\(f\)を連続な関数とすると、次の等式が成り立つ。

\[ \begin{aligned}\int _0 ^1 f(x) dx = \lim_{n\to \infty} \frac{1}{n} \sum _{k=1}^n f(\frac{k}{n})\end{aligned} \]

区間の幅が\(\frac{1}{n}\)であり、\(k\)個目の小区間における長方形の高さが\( f(\frac{n}{k})\)です。したがって近似する長方形の面積を合計は\(\frac{1}{n} \sum _{k=1}^n f(\frac{n}{k})\)で、その極限が面積としての積分の定義となります。

高校数学では、数列の極限を求めるために区分求積法を用いる問題が出題されます。極限値の問題を積分に置き換えて、積分を原始関数によって計算することで極限値を求めるという流れです。

これはやや奇妙な問題です。本来は、区分求積法（によって表される和の極限）が、グラフの面積、積分の定義です。積分法の応用問題として、よくわからない数列の極限値を求めさせようとするのは論理の順番が逆転しています。そこで問題にされている数列は、特定の関数の上限和ないし下限和で、その極限を求めるということは、原理によって積分を計算せよという問題です。

例えば、\(f(x)=x^2\)の上限和の極限値は、数列の和の公式を使うことで求められます。\(f(x)=e^{x}\)も、等比数列の和の公式によって極限値が計算できます。こうした極限値を求めることによる原理的な積分計算のことを、区分求積法と呼ぶのが適切ではないでしょうか。（なので、高校流の区分求積法の説明がよくわからなくても気にしないで良いでしょう）

参考：杉浦「解析入門 Ⅰ」 p.219

区分求積法では、区間の分割の幅は一定であり、小区間において\(f\)を代表する値を右側端点\(f(\frac{k}{n})\)としています。

より一般には、分割の幅が一定でなくても、小区間を代表する点が右側端点でなくても、積分と呼ばれる量が定まっていてほしいです。これはきちんと定義できて、リーマン積分（Riemann integral）と呼ばれています。高校で学ぶ積分は、リーマン積分だったわけです。

参考：杉浦「解析入門 Ⅰ」 p.206

（有界な閉区間で）連続な関数は、リーマン積分ができること、分割の仕方や代表点の選び方によらず極限値が定まることが知られています。さらに、

微積分学の基本定理（ fundamental theorem of calculus）

\(f\)を\(a\leq x \leq b\)において微分可能な関数で、導関数が連続であるならば、次の等式が成り立つ。

\[ \begin{aligned}\int _a ^b f^{\prime}(x) dx =f(b)-f(a)\end{aligned} \]

がリーマン積分の定義から証明できます。それは、上で行った平均値の定理を利用した計算とほぼ同じです。

今回は、\(\sin x\)のグラフの「面積」を長方形によって近似計算しました。その近似を細かくしていくと、確かにある一定の値に収束しましたが、それが面積による積分の定義です。

区分求積法は積分計算のひとつの方法であり、一般にはリーマン積分と呼ばれる方法で積分の理論は展開されていきます。そこからは確かに、積分の値が原始関数によって計算できるという微分積分学の基本定理が導けるのです。だから、高校では「積分は微分の逆」として定義して計算して良かったのですね。

微分方程式の解をコンピュータを使って近似的に解くときには、積分計算が必要になりますが、そこでは積分を長方形や台形で近似します（オイラー法）。