ストゥルム・リウビル型微分方程式の発見：熱方程式から

どうも、木村（@kimu3_slime）です。

今回は、常微分方程式に関して知られるストゥルム・リウビル型微分方程式のあるケースが、熱方程式から導かれることを紹介します。

前提知識：熱方程式の解き方：変数分離法、フーリエ級数展開（1次元、有界領域）

ストゥルム・リウビル型微分方程式とは
熱方程式とストゥルム・リウビル型微分方程式
こちらもおすすめ

ストゥルム・リウビル型微分方程式とは

そもそも、ストゥルム・リウビル（Sturm–Liouville）型の微分方程式とは、

\[ \begin{aligned}\frac{d}{dx}(p(x) \frac{dw}{dx}(x)) + \{q(x)+ \lambda r(x)\}w(x) =0\end{aligned} \]

\[ \begin{aligned}\alpha_1 w(a)+ \alpha_2 \frac{dw}{dx}(a)=0\end{aligned} \]

\[ \begin{aligned}\beta_1 w(b)+ \beta_2 \frac{dw}{dx}(b)=0\end{aligned} \]

と表される\(w\)に関する常微分方程式です。

ここで、変数\(x\)は\(\mathbb{R}\)の有界な閉区間\([a,b]\)上で動き、\(p,q,r\)は連続関数、\(\lambda,\alpha_1,\alpha_2,\beta_1,\beta_2\)は定数です。

\(w \equiv 0\)という常に方程式を満たす、自明解が存在していますね。

\(\lambda\)をパラメータと考え、その\(\lambda\)に対して方程式に非自明な解\(w\)が存在するとき、その\(\lambda\)を固有値、対応する解\(w\)を固有関数と呼びます。

そして、次の結果が知られています。（ストゥルム・リウビルの理論）

固有値は可算無限個存在し、すべて実数である。その最小のものを\(\lambda _0\)とすると、
\[ \begin{aligned}\lambda _0 < \lambda_1 <\lambda_2 <\cdots\end{aligned} \]
で、\(\lambda_n \to \infty (\mathrm{as}\; n\to \infty)\)。
各固有値\(\lambda_k\)に対応する固有関数は（定数倍を除き）唯一つ。（＝固有空間の次元は1）
異なる固有関数は\(r\)の重み付き内積に関して直交する\(\int_a ^b r(x)w_k w_n dx=0 \)。（さらに、重み\(r\)つきの\(L^2\)空間の完全正規直交基底となる。）
固有関数\(w_k\)は、\((a,b)\)においてちょうど\(k\)個のゼロ点を持つ。

参考：柳田-栄「常微分方程式論」4.4

用語について：無限集合の多さ（濃度）はどのくらい？可算無限、カントールの対角線論法とは、線形代数の応用：関数の「空間・基底・内積」を使ったフーリエ級数展開

常微分方程式論でこの結果を知ったとき、色々なことがわかって面白いなと思いましたが、どんな応用から導かれたものか想像できませんでした。

その単純なケースとしては、\(p\equiv 1,q\equiv 0 , r \equiv 1\)とすれば、

\[ \begin{aligned}\frac{d^2 w}{dx^2}(x) + \lambda w(x) =0\end{aligned} \]

の境界値問題です。かなりシンプルになりました。

今回はこれを、1次元の熱方程式から導いてみます。

熱方程式とストゥルム・リウビル型微分方程式

1次元の有界区間\([0,1]\subset \mathbb{R}\)における、次のような熱方程式を考えましょう。

\[ \begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial u}{\partial t} &=& \Delta u & \text{in } (0,1)\times (0,\infty) \\ u(0,t) &=&0 & \\ u_x(1,t) &=& -u(1,t)& \\ u &=&g& \text{on } (0,1)\times \{t=0\} \\ \end{array} \right. \end{aligned} \]

ここで、\(\Delta u = \frac{\partial ^2 u}{\partial x^2}\)です。

まず境界条件に注目してみます。

以前は、\(u(0,t)=u(1,t)=0\)というディリクレ境界条件を考えました。これはシンプルです。

今回は、一方はディリクレですが、もう一方は\(u_x\)（境界における法線微分）を指定するノイマン境界条件（Neumann boundary condition）とディリクレをあわせた境界条件を考えています。これをロバン境界条件（Robin boundary condition）と呼びます。

ノイマン境界条件は、境界における熱の出入り具合を指定するものです。\(u_x=0\)ならば、断熱された状況ができあがります。

ロバン境界条件は、熱の出入りはあるが、その出入り具合は境界における温度に依存するというもの。ディリクレ単体のように境界の温度が外部の温度と常に一致するわけではなく、かといってノイマン単体のように熱の出入りが一定であるわけでもなく、内外で温度に応じた熱の出入りが行われます。これはニュートンの冷却法則（Newton’s law of cooling）に対応した条件です。

ここでストゥルム・リウビル型常微分方程式の境界条件を思い出してみると、

\[ \begin{aligned}\alpha_1 w(a)+ \alpha_2 \frac{dw}{dx}(a)=0\end{aligned} \]

\[ \begin{aligned}\beta_1 w(b)+ \beta_2 \frac{dw}{dx}(b)=0\end{aligned} \]

ロバン境界条件になっています。この境界条件は複雑に見えるかもしれませんが、ディリクレ境界条件とノイマン境界条件を組み合わせたものと見れば、怖くありませんし自然なものです。

さて、熱方程式からストゥルム・リウビル型微分方程式を導いてみましょう。

変数分離法、固有関数展開を目標とする中で、すぐに登場してきます。

解\(u\)が\(u(x,t)=v(t)w(x)\)と変数分離できたと仮定しましょう。これを熱方程式に代入すると、

\[ \begin{aligned} v'(t) w(x) = v(t) \Delta w (x)\end{aligned} \]

となります。

今、自明でない解\(u\not \equiv 0\)について考えているので、\(v(t_0)w(x_0)\neq 0\)なる\(t_0,x_0\)が存在します。その点で両辺を割ると

\[ \begin{aligned} \frac{v'(t_0)}{v(t_0)} = \frac{ \Delta w (x_0)}{w(x_0)}\end{aligned} \]

です。両辺の値を\(-\lambda\)と置きましょう。すると、一方の変数だけを元の式に代入することで

\[ \begin{aligned}v'(t) =-\frac{ \Delta w (x_0)}{w(x_0)} \lambda v(t)=-\lambda v(t)\end{aligned} \]

\[ \begin{aligned}\Delta w (x) =-\frac{ v’ (t_0)}{v(t_0)} w(x)=-\lambda w(x)\end{aligned} \]

という2つの常微分方程式が得られました。今回は空間1次元なので、\(\Delta w(x)=\frac{d^2 w}{dx^2}\)です。2番目の常微分方程式が、ストゥルム・リウビル型微分方程式の特殊なケースです。

境界条件について。

まず\(u(0,t)=v(t)w(0)=0\)で、\(v\)は自明でないものを考えているので、\(w(0)=0\)となります。

また、\(u_x(1,t)+u(1,t)=v(t)\frac{dw}{dx}(1)+v(t)w(1)=0\)です。\(v(t)(\frac{dw}{dx}(1)+w(1))=0\)で、\(v\)は非自明なので、\(\frac{dw}{dx}(1)+w(1)=0\)が言えます。

以上によって、熱方程式から導かれた\(w\)に関する常微分方程式は、

\[ \begin{aligned}\frac{d}{dx}(1 \cdot \frac{dw}{dx}(x)) + \{0+ \lambda \cdot 1\}w(x) =0\end{aligned} \]

\[ \begin{aligned}1\cdot w(0)+ 0\cdot \frac{dw}{dx}(0)=0\end{aligned} \]

\[ \begin{aligned}1\cdot w(1)+ 1\cdot \frac{dw}{dx}(1)=0\end{aligned} \]

とストゥルム・リウビル型微分方程式を満たすことがわかりました。

このあと熱方程式を解くためには、このあと常微分方程式の固有値と固有関数を求め、それを使って一般解を固有関数展開（フーリエ級数展開）することになります。

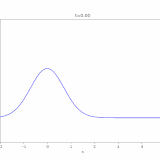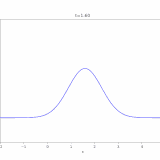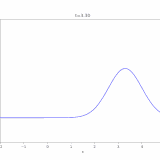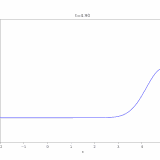
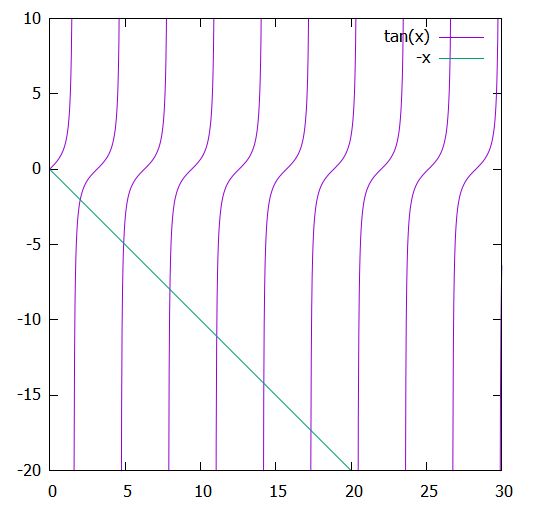
これは以前に紹介した熱方程式の解法と似ているので、省略します（固有値が、ロバン境界条件によって、\(\tan \sqrt{\lambda} = -\sqrt{\lambda}\)を満たすものになる。明示的に求めにくいが、\(\lambda _0 < \lambda_1 <\lambda_2 <\cdots\)となることはわかる。下図のグラフの交点の2乗が固有値。）。