どうも、木村(@kimu3_slime)です。
数学科では2年次の授業とされる群論は、代数方程式の可解性の判別のために生み出されましたが、図形や物理法則・物質の対称性を調べるために、幾何学・物理学・化学にも応用されています。
今回は、そんな群論の初歩的な部分を、回転群と巡回群を例に解説していきます。
(この記事では、集合論、線形代数の基礎を前提知識とします。)
目次
群とは何か
おおざっぱに言って、群とは何でしょうか。
数学的には、ものの集まり(集合)と、その要素間の関係性(構造)をあわせたものが群です。
物事の対称性を「構造」として取り出す。すると、個別具体のものにとらわれずに、本質的に同一であったり/異なったりするかどうかがわかる。この(群論的な)構造こそが群のアイデアです。
ちょっと抽象的に話しましたが、より具体的に見ていきましょう。
有限回転群 \(F_nSO(2)\)
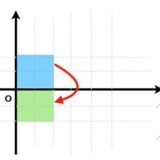
まず、図形の回転に潜む「構造」に注目してみます。
線形代数的に
例えば、ある正三角形をそれ自身に重ねるような平面上の回転変換を考えてみましょう。
\[ \begin{aligned}A_k=\begin{pmatrix} \cos (\frac{2\pi k}{3}) & -\sin (\frac{2\pi k}{3}) \\ \sin (\frac{2\pi k}{3}) & \cos (\frac{2\pi k}{3}) \end{pmatrix} \end{aligned} \]
\(k=1\)なら\(120^{\circ}\)の回転、\(k=2\)なら\(240^{\circ}\)。\(k=3\)なら\(360^{\circ}\)ともとに戻ってきます。

図形描写の参考:【python】matplotlibで正多角形や円を描写する – tomowarkar
正三角形ではなく、一般の正\(n\)角形ならどうなるでしょうか。一周\(2\pi\)を\(n\)で割った角度で回転させても等しいのですから、
\[ \begin{aligned}A_k=\begin{pmatrix} \cos (\frac{2\pi k}{n}) & -\sin (\frac{2\pi k}{n}) \\ \sin (\frac{2\pi k}{n}) & \cos (\frac{2\pi k}{n}) \end{pmatrix} \end{aligned} \]
という回転行列を考えることになります。
抽象的に
回転行列\(A_k\)には、ある種の規則性があることはすぐにわかると思います。
\(n=3\)の場合、\(A_0=A_3=E,A_1=A_4,A_2=A_5\)といったように。(\(E\)は単位行列、つまり何も回転させないということ)
つまり、\(A_k\)といっても本質的に異なるのは、\(E,A_1,A_2\)だけというわけです。
そして、これらの間では積(回転の合成)が計算できます。つまり、\(A_1 A_1 =A_2, A_1 A_2 =E\)といったように。
そこで、意味のある変換を集めて、有限回転群
\[ \begin{aligned}F_3 SO(2):=\{E,A_1,A_2\}\end{aligned} \]
\[ \begin{aligned}F_n SO(2):=\{E,A_1,A_2,\dots,A_{n-1}\}\end{aligned} \]
と呼ぶことにしましょう。回転群で見られた計算の規則性は、他のものでも見られることを続いて紹介します。
(ちなみに、今回は回転変換のみしか考えていないことに注意してください。平面の\(n\)角形をそれ自身に移す変換としては、回転の他に、対称変換・鏡像変換が抜けています。回転、鏡映を合わせた群は、二面体群\(D_n\)と呼ばれます。)
(\(F_n SO(2)\)という記号は一般的ではないかもしれません。\(SO(2)\)は、2次の回転行列のなす群で、特殊直交群と呼ばれます。一般には\(SO(n)\)です。\(F_n SO(2)\)は、回転のうち有限的なものを集めたものです。さらにより広く正則な線形変換全体を考えると、一般線形群\(GL(n)\)と呼ばれます。)
加法巡回群 \(\mathbb{Z} / n\mathbb{Z}\)
正三角形の変換で見られた規則\(A_0=A_3=E,A_1=A_4,A_2=A_5\)を見ていると、何か倍数的なものを感じます。
この倍数的な側面を取り出す計算規則が、整数の合同です。
整数\(a,b\)が\(n\)を法として合同であるとは、\(a-b\)が\(n\)で割り切れることと定義し、これを\(a \equiv b \,(\mathrm{mod} \, n)\)と書きます。
例えば、\(1 \equiv 4\, (\mathrm{mod}\, 3),2 \equiv 5\, (\mathrm{mod}\, 3)\)です。合同算術は、一周する時計盤や、\(n\)進数のように説明されます。
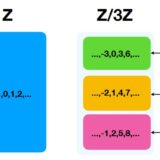
このような合同関係を考えると、整数\(\mathbb{Z}\)はより少ない要素に還元されます。それを
\[ \begin{aligned}\mathbb{Z} / 3\mathbb{Z}:=\{\overline{0},\overline{1},\overline{2}\}\end{aligned} \]
\[ \begin{aligned}\mathbb{Z} / n\mathbb{Z}:=\{\overline{0},\overline{1},\overline{2},\dots,\overline{n-1}\}\end{aligned} \]
と書きます。
ここで合同算術にのっとった足し算\(+\)を考えると、
\(n=3\)のとき、\(\overline{1}+\overline{1}=\overline{2},\overline{1}+\overline{2}=\overline{0}\)といった計算規則が成立しています。これはさきほどの回転行列とそっくりですね。
このような計算規則を備えた集合を、加法巡回群\(\mathbb{Z} / n\mathbb{Z}\)と呼びます。
(\(p\)を素数として、\(F_p:=\mathbb{Z} / p\mathbb{Z}\)は有限体と呼ばれ、暗号理論などに応用されています。参考:有限体の応用– RSA暗号 – 神戸大学)
(\(1 \equiv 4\, (\mathrm{mod}\, 3)\)のように、もとの集合の異なる要素を関係\(\equiv\)によって同一視して新しい集合を作る操作は、商集合、商群と呼ばれます。\(\mathbb{Z} / n\mathbb{Z}\)は、整数\(\mathbb{Z}\)を\(n\)の倍数\( n\mathbb{Z}\)で割って同一視しているわけです。参考:商集合、同値関係・同値類を解説~商群の理解に向けて)
巡回置換群 \(C_n\)
さきほどとは別の視点で、正三角形の回転変換を捉えてみましょう。
下図のように、三角形の頂点を\(a,b,c\)とします。回転という操作は、頂点の記号\(a,b,c\)の入れ替え操作としても見ることができますね。
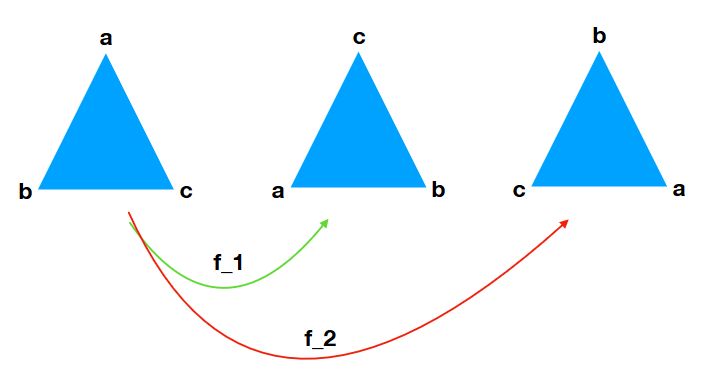
つまり、入れ替え操作\(f_1\)とは、関数\(f_1:\{a,b,c\}\to\{a,b,c\}\)で、\(f(a)=c,f(b)=a,f(c)=b\)とも言えるわけです。入れ替え操作をわかりやすく表すために、
\[ \begin{aligned}f_1=\begin{pmatrix} a & b & c\\ c& a& b \end{pmatrix} \end{aligned} \]
と書かれることがあります(行列とは違います)。もとは上の列の記号が、下の列の記号へ入れ替えられるわけです。このような入れ替え操作全般を、置換(permutation)と呼びます。
(数学的には、置換とは、有限集合\(X\)からそれ自身への全単射な写像のことです。それらを集めたものを、対称群・置換群\(S_n\)と呼びます。)
\(f_1\)と同様に上図の置換を\(f_2\)、何も入れ替えないという置換(恒等写像)を\(e\)と表すことにします。
置換の間に働く計算規則は、さきほどの行列の積や合同数の和ではなく、写像の合成\(\circ\)です。\(f_1\)の入れ替えを2回行うことは\(f_2\)である\(f_1\circ f_1=f_2\)ことは、図を見れば明らかで、写像の合成を計算してみてもわかります。
こうして得られる
\[ \begin{aligned}C_3:=\{e,f_1,f_2\}\end{aligned} \]
\[ \begin{aligned}C_n:=\{e,f_1,f_2,\dots,f_{n-1}\}\end{aligned} \]
を巡回置換群\(C_n\)、あるいは単に巡回群と呼びます。置換という入れ替え操作のうち、何回も操作すると輪っかのように戻ってくる特殊な置換(巡回置換)を集めたわけです。
群の定義、群論的な構造
有限回転群\(F_nSO(2)\)、加法巡回群 \(\mathbb{Z} / n\mathbb{Z}\)、巡回置換群 \(C_n\)には、共通する計算の規則があります。それが群と呼ばれる理由です。
群(group)とは、集合\(X\)とその上の二項演算\(*:X\times X \to X\)(と呼ばれる写像)の組\((X,*)\)で、次のような性質を満たすものです。
(G1)演算について閉じている:\(x_1,x_2\in X\)に対し、\(x_1*x_2\in X\)
(G2)結合法則:\(x_1,x_2,x_3\in X\)に対し、\((x_1*x_2)*x_3=x_1*(x_2*x_3)\)
(G3)単位元の存在:次のような元\(e \in X\)が存在する。任意の\(x_1\in X\)に対し、\(x_1*e=e*x_1 =x_1\)
(G4)逆元の存在:任意の\(x_1\in X\)に対し、\(x_1*x_1^{-1}=x_1^{-1}*x_1 =e\)を満たすような\(x_1^{-1} \in X\)が存在する。
今まで考えてきた、行列の積(記号で表されない)、\(n\)を法とした加法\(+\)、置換の合成\(\circ\)を、二項演算\(*\)として抽象化しました。\(*\)は慣例的に積と呼ばれることが多いですが、数の積を必ずしもイメージするわけではありません。こうすることで、\(*\)によって表されているものが掛け算・足し算・合成だろうが、関係なく成立している共通の演算規則が取り出せているわけです。
(G1)、(G2)は閉じた計算規則が成り立っていることを表すもので、例えば置換の合成は置換になっています。
(G3)は、何も影響を与えない要素\(E,\overline{0},e\)を抽象化したもので、これは単位元(unit element)と呼ばれます。
(G4)は、すべての操作に対し、それをもとに戻す操作(逆元 inverse element)も必ず含まれていることを要請しています。例えば\(\mathbb{Z} / 3\mathbb{Z}\)において、\(\overline{1}+\overline{2}=\overline{0}\)なので、\(\overline{1}\)の逆元は\(\overline{2}\)です\((\overline{1})^{-1}=\overline{2}\)。
自然数の集合\(\mathbb{N}\)で足し算の演算を考えたとき、逆元は自然数内に存在しないので、群ではありません。整数\(\mathbb{Z}\)で足し算を考えれば群です(加法群)。しかし整数\(\mathbb{Z}\)で掛け算を考えれば、逆元が存在しないので(分数になる)、群ではありません。群かどうか考えるときには、考えている集合だけでなく、考えている演算は何かを意識しましょう。
(G1)-(G4)に加え、
(G5)交換法則:\(x_1,x_2\in X\)に対し、\(x_1*x_2=x_2*x_1\)
が成り立つ群を可換群(commutative group)、またはアーベル群(Abelian group)と呼びます。今回見てきた多くの群は可換ですが、二面体群\(D_n\)や(一般の)行列群、対称群\(S_n, \, n\geq3\)は可換ではありません。
また、群\((X,*)\)が与えられたとき、\(X\)の部分集合\(Y\)であって、かつ\(Y\)が\(*\)について群であるとき、\(Y\)は\(X\)の部分群(subgroup)であるといいます。
例えば、巡回置換群 \(C_n\)は対称群\(S_n\)の部分群です。巡回置換同士の合成がきちんと巡回置換になっているので、群として閉じています。
群は、集合とその上の二項演算によって定義されますが、これらは合わせて代数的構造(algebraic structure)とも呼ばれます。
群はかなりシンプルな代数的構造です。他にも有名な構造として、環(かん ring)、体(たい field)、加群(かぐん module)などがあります。これらを扱う分野は、代数系、あるいは抽象代数学(abstract algebra)と呼ばれ、大学の数学科では2-3年次に教えられることが多いです。
環上の加群は、ベクトル空間(線形空間)を一般化したものです。逆に、線形代数学は、環上の加群の理論の一部分として見ることもできるでしょう。こうした理由もあって、抽象的な代数学を学ぶ前に、一年次に線形代数を学ぶことになっているのだと思います。
今回扱った構造は代数的構造と呼ばれるもので、数学では他にも、位相的構造や順序的構造を考えることがあります。群の構造は代数的構造の基礎なので、まずここから理解する価値はあると思います。
参考:集合、構造、空間とは何か? ユークリッド空間\(\mathbb{R}^N\)を例に考える
群として同型
群論の際立ったアイデアのひとつが、同型という考え方です。一見異なる集合に見えても、元と計算規則を見れば本質的には同じ群だよね、と言えるわけです。
群\((G_1,*_1),(G_2,*_2)\)が群として同型である\(G_1 \simeq G_2\)とは、全単射な写像\(F:G_1\to G_2\)で、
\[ \begin{aligned}\forall g_1,g_2\in G_1\quad F(g_1*_1 g_2)= F(g_1)*_2 F( g_2)\end{aligned} \]
が成り立つものが存在することを言います(左辺と右辺で考えている演算が違うことに注意)。
写像\(F\)は、群\((G_1,*_1),(G_2,*_2)\)の演算まで含めての対応関係の述べるもの、つまり群としての構造を保つ写像で、同型写像(homomorphism)と呼ばれます。
(全単射の条件を外し、演算の両立のみの場合は、準同型 isomorphism と呼ばれます。)
(2つの位相空間が「同じ」であることを示す写像は、位相同型写像と呼ばれます。同型というアイデアは数学全般に見られるもので、圏論と呼ばれる分野では同型射として一般化されています。)
ここまで準備が整ったので、有限回転群\(F_nSO(2)\)、加法巡回群 \(\mathbb{Z} / n\mathbb{Z}\)、巡回置換群 \(C_n\)が同型であることが言えます。
写像\(F_1:F_nSO(2)\to \mathbb{Z} / n\mathbb{Z}\)を、\(F_1(A_k):=\overline{k}\)と定めましょう。\(k=0\)のときは\(F_1(E):=\overline{0}\)です。要素がすべて対応しており、全単射なのは明らかでしょう。
\(j,k\in \{0,1,\dots,n-1\}\)として、
F_1(A_k A_j)&= F_1(A_{k+j} ) &= \overline{k+j}\\
F_1(A_k)+F_1 (A_j)&=\overline{k}+\overline{j}&=\overline{k+j}
\
なので、\(F_1\)は同型写像であり、\(F_nSO(2)\simeq \mathbb{Z} / n\mathbb{Z}\)が言えました。同様にして、\(\mathbb{Z} / n\mathbb{Z} \simeq C_n\)も言えます(試してみてください)。
こうして、\(F_nSO(2)\simeq \mathbb{Z} / n\mathbb{Z}\simeq C_n\)の間は自由に行き来・翻訳できることがわかりました。
逆に、これらは加法群\(\mathbb{Z}\)とは同型ではありません。一方は有限集合で、もう一方は無限集合であり、全単射が存在しないからです。
もしある場所で見つかった群が、既に知っている群に同型であることがわかれば、既存の群の性質を使って分析できるわけです。対象に潜む代数的な計算規則を取り出し、既知の群と同型であることを示して分析できる、これが群論の強みですね。
(有限回転群\(F_nSO(2)\)では、その要素が行列として表されていました。一般的な群\(G\)の各要素を、正則行列として表すことを群の表現と呼びます。表現をすれば、線形代数・行列的な枠組みを使って、群を分析できるわけです。表現を詳しく扱う分野は表現論と呼ばれ、多くの応用や研究が生み出されています。)
群の生成、有限生成群、元の位数
これでおよそ群論入門としてのお話はできたと思うので、以降は補足的なざっくりとした話です。
\( \mathbb{Z} / n\mathbb{Z}\)においては、\(\overline{1}+\overline{1}=\overline{2},\overline{1}+\overline{1}+\overline{1}=\overline{0}\)と、要素\(\overline{1}\)を繰り返し足していく(または逆元を加えていく)ことで群全体が得られます。これを、\( \mathbb{Z} / n\mathbb{Z}\)は部分集合\(\{\overline{1}\}\)によって生成されると呼びます。
一般に、\(S\)を群\(G\)の部分集合として、\(S\)の逆元全体を\(S^{-1}\)と表すことにします。そして\(H\)を、\(S\cup S^{-1}\)の有限個の元の積によって表される元の集合とすると、\(H\)は\(G\)の部分群となります。このとき、\(H\)は\(S\)によって生成されると言い、\(S\)を生成系と呼びます。特に、有限集合によって生成される群を、有限生成と呼びます。
加法群\(\mathbb{Z}\)は、有限集合ではありませんが、有限生成です(1によって生成される)。また、要素が有限個の群(有限群)は、当然有限生成です。つまり、有限生成群は、有限群だけでなく無限群を含むけれども、ある種の有限性を持った群と言えます。
そして、\(g^k =e\)となる最小の自然数\(k\)を元\(g\)の位数(order)と呼びます。(\(g^k\)は、\(g\)を演算\(*\)で\(k\)回掛けたもの)
\( \mathbb{Z} / n\mathbb{Z}\)において、元\(\overline{1},\overline{2}\)の位数はともに3ですね。加法群\(\mathbb{Z}\)において元\(1\)の位数は、存在しません(これを位数は無限と呼びます)。
こうした群の生成や、元の位数といった情報も、同型写像によって保たれます。群の言葉で書かれた性質は、同型な群については同様に成り立つわけです。便利ですね。
有限アーベル群の基本定理
今回紹介したような巡回群(有限回転群)は、群の分解単位として基本的なものと言えます。
有限アーベル群の基本定理
有限生成のアーベル群は、有限個の巡回群の直積群に同型である。
参考:堀田「代数入門―群と加群」p.75, 有限アーベル群の構造定理 – Wikipedia
もちろん、一般の群は有限生成とは限りません。しかし、有限生成の群に関しては、巡回群によって「分解」できるわけです。
今回は、有限回転群\(F_nSO(2)\)、加法巡回群 \(\mathbb{Z} / n\mathbb{Z}\)、巡回置換群 \(C_n\)を例に、群の定義、同型の概念などを紹介してきました。実はこれらは同型で、群としては本質的に同じものとして扱って良いということがわかりました。
巡回群は有限集合(有限群)であり、非常にシンプルな計算規則を持っているので、群論入門としてはまずこれを抑えてから進むと、地に足のついた理解が進むのではないかと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
図形の対称性を記述する二面体群、多面体群、点群・結晶群について解説
無限集合の多さ(濃度)はどのくらい? 可算無限、カントールの対角線論法とは