力学系の構造安定性について簡単に紹介

どうも、木村（@kimu3_slime）です。

力学系理論における構造安定性という概念について、簡単に紹介したいと思います。

解の安定性に関する前提知識はこちら：方程式を解かずに、解の軌跡・安定性を調べてみよう力学系理論入門

構造安定性＝摂動によって系の性質が変化するか？
力学系が「似ている」とはどういうことか？
構造安定性の定義、性質
こちらもおすすめ

構造安定性＝摂動によって系の性質が変化するか？

構造安定性は、ざっくり言えば、「ある微分方程式の力学系は、その微分方程式をほんの少し変化させたときに、同じような振る舞いをするかどうか？」を捉える概念です。

平衡解の安定性と混同しないように注意しましょう。解の安定性は、ある方程式を決めて、その中で特定の解が初期値の変化について安定かどうか論じるものでした。一方で、構造安定性は、方程式の変化について解の挙動が安定かどうか論じるものです。

数式で言えば、\(\dot{x} =f(x) \quad x\in \mathbb{R}^N\)に対して、それをほんの少し「動かした」\(\dot{x}=f(x)+ \varepsilon g(x)\)を考え、解の安定性などの性質が変化するかどうか問います。

このときに、加える小さな変化を摂動（perturbation パタベーション）と言います。日本語としてはあまり馴染みがないかもしれませんが、撹乱するといった意味です。

摂動を与える項\(\varepsilon\)を摂動項、\(\varepsilon=0\)のときをあえて非摂動問題（unperturbed problem）ということがあります。

力学系が「似ている」とはどういうことか？

ある力学系とその摂動された力学系という、2つの力学系を考え、その2つが「似ている」ならば構造安定、「似ていない」ならば構造不安定と定義したいです。

この「似ている」ということは、数学では、位相的同値性によって定義されます。

2つの力学系が定める流れ flow を\(\varphi_t,\psi _t\)とします。

\(\varphi_t,\psi _t\)が位相的に同値（topologically equivalent）であるとは、同相写像\(h:\mathbb{R}^N \to \mathbb{R}^N\)で、時間の向きを保ちながら一方の解をもう一方に移すものが存在することです。

（同相写像とは、全単射な連続写像で、その逆写像も連続であるものです。）（位相的に同値という関係は、同値関係になっています。）

少し例を見てみましょう。

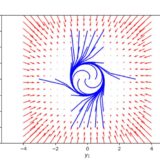
\[ \begin{aligned} \left\{ \begin{array}{l} \dot{x} =-x \\ \dot{y} =-y \end{array} \right.\end{aligned} \]

\[ \begin{aligned} \left\{ \begin{array}{l} \dot{x} =-x-y \\ \dot{y} =x-y \end{array} \right.\end{aligned} \]

第2式は、\(\varepsilon=1, g(x,y)=(-y,x)\)としたときの第1式の摂動です。

この方程式は、簡単に解くことができて、解は一方を回転させたものになっており、位相的に同値です。

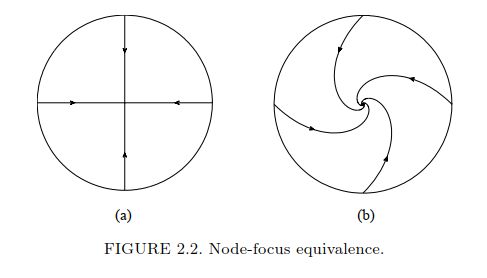
画像引用：Kuznetsov Elements of Applied Bifurcation Theory

解の流れ自体は歪んでいますが、平衡解が安定であるという性質は変わっていませんね。どちらも、線形化行列の固有値の実部が負です。

より一般に、次のことが言えます。

\(\dot{x} =f(x) \quad x\in \mathbb{R}^N\)と\(\dot{x}=f(x)+ \varepsilon g(x)\)という2つの方程式を考え、\(f\)に不動点\(\bar{x}\)があるとします。そして、不動点での線形化行列の固有値の実部がすべて0でないとします（このような不動点を、双曲型不動点 hyperbolic fixed pointという）。このとき、十分小さい近傍を考えれば、2つの方程式は位相的に同値となります。

つまり、「双曲型の平衡点は、なめらかな摂動に対して構造安定」です。

一方で、小さな摂動をしても位相的に同値にならないケースもあります。

\[ \begin{aligned} \left\{ \begin{array}{l} \dot{x} =y \\ \dot{y} =-x \end{array} \right.\end{aligned} \]

\[ \begin{aligned} \left\{ \begin{array}{l} \dot{x} =y \\ \dot{y} =x-\varepsilon y \end{array} \right.\end{aligned} \]

線形化行列の固有値を調べれば、上の方程式の平衡解はリヤプノフ安定であるが漸近安定でないにもかかわらず、下の方程式では漸近安定になっていることがわかります。

上の方程式の周期解が下では存在せず、対応が存在しません。位相的に同値ではありません。

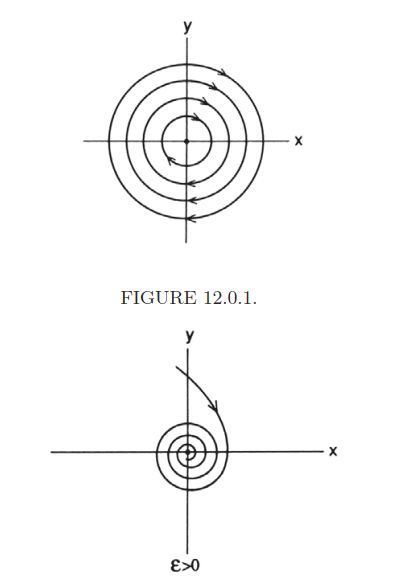
画像引用：Introduction to Applied Nonlinear Dynamical Systems and Chaos

つまり、上の方程式は「構造安定」ではありません。

構造安定性の定義、性質

では、構造安定性の定義を紹介しましょう。

\[ \begin{aligned}\dot{x}=f(x)\quad x\in \mathbb{R}^N\end{aligned} \]

力学系が（狭義の）構造安定である（structurally stable）とは、\(f\)の\(C^1\)位相での近傍\(U\subset C^1\)で次のようなものが存在すること。任意の\(g\in U\)は\(f\)に位相的に同値。

\(C^1\)位相での近傍とは、

\[ \begin{aligned}d(f,g)=\sup_{x\in U} \{ \|f(x)-g(x)\|+ \| \frac{df}{dx}(x) +\frac{dg}{dx}(x) \| \}\end{aligned} \]

という距離を考えています。

構造安定性について、一般に次のような定理が知られています。

定理 Andronov, Pontryagin [1937]
\(N=2\)とし、連続な力学系
\[ \begin{aligned}\dot{x}=f(x)\end{aligned} \]
を考える。
力学系が領域\(D\subset \mathbb{R}^2\)において構造安定であることは、次のことと同値。
i) \(D\)には有限個の平衡点とリミットサイクルがあり、それらがすべて双曲型。
ii) 同じサドルに戻る、または異なるサドルをつなぐようなサドル・セパラトリクスが存在しない。

参考：Elements of Applied Bifurcation Theory、Andronov, Aleksandr A.; Lev S. Pontryagin (1937). “Грубые системы” [Coarse systems]. Doklady Akademii Nauk SSSR. 14 (5): 247–250.

サドル・セパラトリクス（separatrix）とは、サドルに出入りする軌道のこと。それを境に解の挙動を分けることからそう呼ばれる。

構造安定性の概念は、もともとこの定理を発見したアンドロノフとポントリャーギンによるもので、当初は粗い系（coarse system）と呼ばれていました。

参考：非線形現象入門 – 川上博

上記の定理は、\(N=2\)のときのみのものです。

高次元の場合は、Morse-Smale 条件と呼ばれる類似の十分条件はありますが、同値条件は成立しないことが知られています。

次の記事で紹介した、馬蹄写像が、構造安定であるが無限個の周期解を持つケースとなっています。

参考：カオス現象のわかりやすい具体例を視覚的に見る

今回は、力学系が似ていることを位相的同値性によって定義し、その例を考え、構造安定性について紹介しました。

これまでの力学系の記事では、微積分と線形代数の知識のみで話が済みましたが、同相写像といった位相空間論的な知識が必要になっています。

逆に言えば、位相空間論の応用として、構造安定性という概念があるとも捉えられるわけです。取っ掛かりがなかったので書いていませんでしたが、少しずつ、位相空間論の記事も増やしていこうと思います。

木村すらいむ（@kimu3_slime）でした。ではでは。