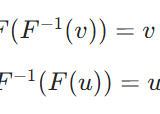どうも、木村(@kimu3_slime)です。
今回は、逆作用素の性質:線形性、固有値、対称性に関する証明を紹介します。
逆作用素の性質
\(X,Y\)をノルム空間、\(D(F)\)を\(X\)の部分空間、\(F:D(F) \to Y\)を線形作用素とします。
\(F\)が可逆作用素であるとき、\(F(u)=v\)が\(u =F^{-1}(v)\)と同値になるような逆作用素\(F^{-1}:R(F)\to D(F)\)を考えることができました。
今回は、\(F\)の条件に応じて\(F^{-1}\)が良い性質を持つことを証明します。
線形性
\(F\)が線形作用素であるとき、\(F^{-1}\)は線形作用素です。
\(\alpha\)をスカラー、\(v_1,v_2 \in R(F)\)とします。値域の定義から、\(u_1,u_2 \in D(F)\)で\(F(u_1)=v_1,F(u_2)=v_2\)を満たすものが存在します。逆作用素の定義から、\(u_1=F^{-1}(v_1),u_2 =F^{-1}(v_2)\)です。
このとき、\(F\)の線形性から、\(F(\alpha u_1 +u_2)=\alpha F(u_1)+F(u_2)=\alpha v_1+v_2\)です。再び逆作用素の定義から、\(F^{-1}(\alpha v_1+v_2)= \alpha u_1+u_2=\alpha F^{-1}(v_1)+F^{-1}(v_2)\)となるので、\(F^{-1}\)の線形性が示せました。
固有値、固有ベクトル
\(H=X=Y\)を内積空間とします。
\(F\)のゼロでない固有値と固有ベクトル\(F(u)=\lambda u\)は、逆作用素において\(F^{-1}(u)= \frac{1}{\lambda} u\)と対応します。つまり、逆作用素の固有値は逆数に、固有関数はそのまま固有関数になっています。
\(F(u)=\lambda u\)の両辺に\(F^{-1}\)を作用させると、逆作用素の性質\(F^{-1}(F(u))=u\)、線形性から\(u= \lambda F^{-1}(u)\)です。よって、\(\lambda\)で割れば\(F^{-1}(u)= \frac{1}{\lambda} u\)です。
\(F(F^{-1}(u))=u\)でもあるので、この議論は逆にたどることができます。
ゼロ固有値\(F(u)= 0 u\)のときを考えましょう。\(F(u)=0\)であり、\(F\)の可逆性(単射性)から\(u=0\)です。これは固有ベクトルの定義(ゼロベクトルでないこと)に反します。つまり、可逆な作用素にはゼロ固有値は存在しません。\(\lambda \neq 0\)と仮定して議論して良いわけです。
対称性
\(F\)が対称作用素ならば、\(F^{-1}\)も対称作用素です。
\(F\)が対称であるとは、\(u,v \in D(F)\)に対し\(\langle u,F(v)\rangle_H=\langle F(u),v\rangle_H\)が成り立つことです。
\(F^{-1}\)が対称であることを示すために、\(v_1,v_2 \in D(F^{-1})=R(F)\)としましょう。値域の定義から、\(F(u_1)=v_1,F(u_2)=v_2\)を満たす\(u_1,u_2 \in D(F)\)が存在します。
したがって、\(F\)の対称性、逆作用素の性質から
\[\begin{aligned} &\langle v_1,F^{-1}(v_2)\rangle_H\\&=\langle F(u_1),F^{-1}(v_2)\rangle_H \\ &= \langle u_1,F(F^{-1}(v_2))\rangle_H\\&= \langle F^{-1}(v_1),v_2\rangle_H \end{aligned}\]
となり、\(F^{-1}\)が対称作用素であることが示せました。
以上、逆作用素の性質:線形性、固有値、対称性に関する証明を紹介してきました。
これらの性質から、\(F\)がコンパクトな逆作用素を持つならば、ヒルベルト・シュミットの定理から固有値に関する情報を引き出すことができます。これについては別記事にて。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)