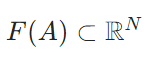1変数の完全正規直交系から2変数の完全正規直交系が作れることの証明

どうも、木村（@kimu3_slime）です。

今回は、1変数の完全正規直交系から2変数の完全正規直交系が作れることの証明を紹介します。

導入
証明
こちらもおすすめ

導入

\(\Omega\)を\(\mathbb{R}^N\)の開集合とし、\((\phi_j)_j\)を\(L^2(\Omega)\)の完全正規直交系、すなわち

すべての\(j\)に対し\(\|\phi_j\|_{L^2}=1\)
\(i \neq j\)ならば\(\langle \phi_i ,\phi_j\rangle_{L^2}=0\)
すべての\(u \in L^2(\Omega)\)に対し、\(u= \sum_{j=1}^\infty \langle u, \phi_j\rangle_{L^2} \phi_j\)

とします。

このとき、その関数系の積として作れる2変数の関数系\((\phi_{k}(x)\phi_\ell(y))_{k,\ell}\)は、\(L^2(\Omega \times \Omega)\)の完全正規直交系となります。

証明

これを証明しましょう。

ノルムや内積を\(\|\cdot\|_{L^2}\)と略記しますが、1変数\(L^2(\Omega)\)なのか2変数なのか\(L^2(\Omega \times \Omega)\)は違うので注意しましょう。

2変数の可積分性、正規性

\(\phi_j \in L^2\)より、フビニの定理（積分の順序交換）が使えます。\(\phi_j\)は正規だったので、

\[\begin{aligned} &\|\phi_{k}(x)\phi_\ell(y)\|_{L^2}^2\\&=\int_{\Omega \times \Omega} \phi_{k}(x)\phi_\ell(y)dx dy \\ &= (\int_{\Omega }\phi_k(x)dx )(\int_{\Omega }\phi_\ell(y)dy) \\&= \|\phi_k\|_{L^2}^2 \|\phi_\ell\|_{L^2}^2 \\&= 1\end{aligned}\]

なので、\(\phi_{k}(x)\phi_\ell(y) \in L^2(\Omega \times \Omega)\)で、\(\|\phi_{k}(x)\phi_\ell(y)\|_{L^2}=1\)です。

直交性

\((k_1 ,\ell_1)\neq ( k_2, \ell_2)\)とします。すなわち少なくとも一方の添字は異なります。\((\phi_j)_j\)の直交性から

\[\begin{aligned} &\langle \phi_{k_1}\phi_{\ell_1},\phi_{k_2}\phi_{\ell_2}\rangle_{L^2} \\ &= \int_{\Omega \times \Omega} \phi_{k_1}(x)\phi_{\ell_1}(y)\phi_{k_2}(x)\phi_{\ell_2}(y)dxdy\\ &= (\int_{\Omega} \phi_{k_1}(x)\phi_{k_2}(x)dx)(\int_{\Omega} \phi_{\ell_1}(y)\phi_{\ell_2}(y)dy)\\&= \langle \phi_{k_1},\phi_{k_2} \rangle_{L^2} \langle \phi_{\ell_1},\phi_{\ell_2} \rangle_{L^2}\\ &=0\end{aligned}\]

です。

完全性

\(k \in L^2(\Omega \times \Omega)\)として、

\[k(x,y)= \sum_{i,j=1}^\infty \langle k, \phi_i \phi_j \rangle \phi_i(x)\phi_j(y) \]

と表せることを示しましょう。

\(x\)を決めて、\(y\)のみを変数とする関数\(v_x(y):=k(x,y)\)に注目します。\(v_x \in L^2(\Omega)\)で、\((\phi_j)_j\)の完全性より\(v_x(y)= \sum_{j=1}^\infty \langle v_x, \phi_j\rangle_{L^2} \phi_j(y)\)と表せます。

逆に\(y\)を決めて、\(u_y(x)= v_x(y)=k(x,y)\)に注目します。\(u_y\in L^2(\Omega)\)で、\((\phi_j)_j\)の完全性より\(u_y(x)= \sum_{i=1}^\infty \langle u_y, \phi_i\rangle_{L^2} \phi_i(x)\)と表せます。

よって、内積の線形性から

\[\begin{aligned} &k(x,y) \\ &= u_y(x) \\&= \sum_{i=1}^\infty \langle u_y, \phi_i\rangle_{L^2} \phi_i(x)\\ &= \sum_{i=1}^\infty \langle v_x(y), \phi_i\rangle_{L^2} \phi_i(x)\\ &=\sum_{i=1}^\infty \langle \sum_{j=1}^\infty \langle v_x, \phi_j\rangle_{L^2} \phi_j(y), \phi_i\rangle_{L^2} \phi_i(x)\\ &= \sum_{i=1}^\infty \sum_{j=1}^\infty \langle \langle v_x, \phi_j\rangle_{L^2} , \phi_i\rangle_{L^2} \phi_i(x) \phi_j(y)\\ &=\sum_{i=1}^\infty \sum_{j=1}^\infty [\int_{\Omega}(\int_{\Omega}k(x,y)\phi_j(y)dy) \phi_i (x) dx]\phi_i(x) \phi_j(y) \\ &=\sum_{i=1}^\infty \sum_{j=1}^\infty [\int_{\Omega\times \Omega}k(x,y)\phi_i (x) \phi_j(y)dxdy]\phi_i(x) \phi_j(y)\\&= \sum_{i,j=1}^\infty \langle k, \phi_i \phi_j \rangle \phi_i(x)\phi_j(y)\end{aligned}\]

が示せました。途中の内積の計算で、\(x\)に関する積分をしているときは、\(\phi_j(y)\)はスカラーとして外に出せることに注意しましょう。

帰納的に、2変数だけでなく多変数であっても、同様の完全正規直交系は作れますね。

以上、1変数の完全正規直交系から2変数の完全正規直交系が作れることの証明を紹介してきました。

これはヒルベルト・シュミット作用素のコンパクト性を示すために、核\(k(x,y)\)を完全正規直交系で分解して議論するために使えます。

木村すらいむ（@kimu3_slime）でした。ではでは。