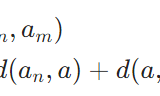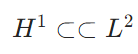距離空間の球面が閉集合であることの証明

どうも、木村（@kimu3_slime）です。

今回は、距離空間の球面が閉集合であることの証明を紹介します。

証明

距離空間\((X,d)\)において、中心\(a \in X\)、半径\(r>0\)の球面を\(S(a,r):=\{u \mid d(a,u)=r\}\)とします。それが閉集合であることを示しましょう。

閉集合の流儀はいくつかありますが、補集合が開集合であることを示しましょう。

開球を\(B(a,r):=\{u \mid d(a,u)<r\}\)と表すことにします。集合\(A\)が開集合とは、すべての\(a \in A\)に対し、\(B(a,R) \subset A\)となるような\(R\)が存在することです。

球面の補集合は

\[X \setminus S(a,r)\\=\{u \mid d(a,u)<r\} \cup \{u \mid d(a,u)>r\}\]

と2つの部分集合に分けられます。

前者は\(B(a,r)\)であり、開球は開集合です。

後者\(\{u \mid d(a,u)>r\}\)も開集合であることを示しましょう。\(b \in \{u \mid d(a,u)>r\}\)とします。そして\(R: =d(a,b)-r\)と置きましょう。\(R>0\)です。

すると、\(B(b,R) \subset \{u \mid d(a,u)>r\}\)が成り立ちます。なぜなら、\(u \in B(b,R)\)とすると、\(d(b,u)<R\)となります。そして、三角不等式から

\[\begin{aligned} & d(a,b)\\ &\leq d(a,u)+d(u,b)\\ &< d(a,u)+R \\&= d(a,u)+d(a,b)-r \end{aligned}\]

となるので、\(d(a,u)>r\)です。よって、\(u \in \{u \mid d(a,u)>r\}\)であり、\(B(b,R) \subset \{u \mid d(a,u)>r\}\)と言えました。

したがって、\(\{u \mid d(a,u)<r\}, \{u \mid d(a,u)>r\}\)はともに開集合です。開集合の和は開集合なので、

\[X \setminus S(a,r)\\=\{u \mid d(a,u)<r\} \cup \{u \mid d(a,u)>r\}\]

は開集合です。補集合が開集合なので、球面\(S(a,r)\)が閉集合と言えました。

別証明として、集合の境界は必ず閉集合となることを示し、開球\(B(a,r)\)の境界が球面\(S(a,r)\)であることを示す、という方法もあります。

今回の議論から、境界を含めた球\(\overline{B(a,r)} =\{u \mid d(a,u)\leq r\} \)も閉集合と言えます。

補集合が\(\{u \mid d(a,u)>r\}\)で、それが開集合だからです。

また、今回は距離空間という一般的な枠組みで示しましたが、ノルム空間や内積空間、ユークリッド空間といった特殊ケースでも球面\(S(a,r)=\{u \mid \|a-u\|=r\}\)は閉集合と言えたことになります。

例えば、数列のなすノルム空間\(\ell ^2\)の単位球（球面）はコンパクトでないという結果は、（有界な）閉集合がコンパクトでないことを示しているわけです。

以上、距離空間の球面が閉集合であることの証明を紹介してきました。

開球が開集合であること、球面が閉集合であることは様々な分野で用いる基本的な性質ですが、それが距離空間という一般的な枠組みで成り立つことを心に留めておきたいですね。

木村すらいむ（@kimu3_slime）でした。ではでは。

関数解析共立数学講座 (15)
黒田成俊(著)
￥4,300 (中古品) (2022-08-21時点)