吸収集合、散逸系とは：線形力学系を例に

どうも、木村（@kimu3_slime）です。

今回は、吸収集合、散逸系とは：線形力学系を例に紹介します。

吸収集合とは
散逸系とは
こちらもおすすめ

吸収集合とは

微分方程式の解の長期的な挙動について調べる理論は力学系と呼ばれますが、その問題のひとつとしてアトラクターがあります。

アトラクターとは、おおざっぱにいえば、周囲の状態を長期的に引き付ける留まり続けるような状態の集合です。

そうしたアトラクターの議論をするために、まずはそれを示唆する集合：吸収集合というものから話を始めましょう。

微分方程式の抽象力学系\((H,(S(t))_{t \geq 0})\)を考えましょう。

相空間\(H\)の部分集合\(B\)が吸収集合（absorbing set）とは、\(H\)の任意の有界集合\(K\)に対して、

\(t \geq t_0\)ならば\(S(t)K \subset B\)

を満たすような\(t_0 \in \mathbb{R}\)が存在することです。時間\(t_0\)は\(K\)に依存して選んで良いです。

イメージとしては、初期値\(u_0\)をベクトル場に沿って流すのと同様に、初期値の集まり\(X\)を流してできる集合\(S(t)K=\{ S(t)u_0 \mid u_0 \in K\}\)を考えています。それが長期的にずっと（\(t \geq t_0\)）含まれ続ける\(S(t)X \subset B\)、それが吸収している集合という意味ですね。

\(H= \mathbb{R}^N\)のときは、吸収集合\(B\)の定義は、任意の\(u_0 \in H\)に対し、「すべての\(t\)に対し、\(t \geq t_0\)ならば\(S(t)u_0 \in B\)」を満たす\(t_0\)が存在する、と定義が弱められることが知られています。

もっと具体的に考えます。

\(H= \mathbb{R}^2\)において、

\[ \begin{aligned} \left\{ \begin{array}{l} \frac{dx}{dt} =-x+y \\ \frac{dy}{dt} =-x-y \end{array} \right.\end{aligned} \]

という常微分方程式が定める解\(S(t) (x_0,y_0)=(x(t),y(t)) \)について考えましょう。

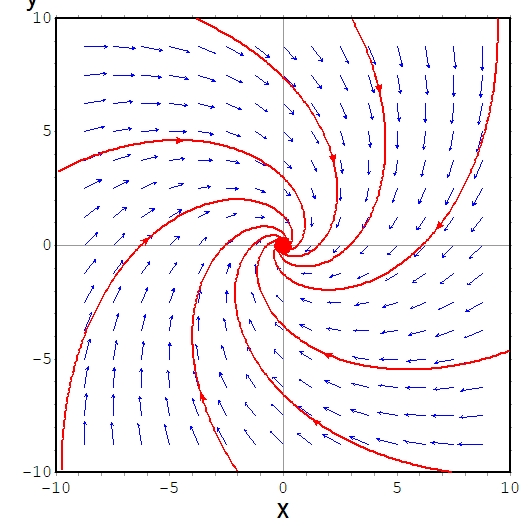
この方程式において、\((x(t),y(t))=(0,0)\)は平衡解であり、大域的に漸近安定です。つまり、どんな初期値\((x_0,y_0)\)に対しても、\(\lim_{t\to \infty}S(t) (x_0,y_0)=(0,0)\)が成り立ちます。これを前提として、吸収集合について考えましょう。

例えば、原点を中心とする円盤\(B_1 =\{(x_0,y_0)\mid x_0 ^2+y_0^2 \leq 1\}\)は吸収集合です。任意の初期値\((x_0,y_0) \in \mathbb{R}^2\)を考えます。\(\lim_{t\to \infty}S(t) (x_0,y_0)=(0,0)\)より、「\(t \geq t_0\)ならば\(x(t)^2 +y(t)^2\leq 1\)」を満たす\(t_0\)が存在します。つまり、「\(t \geq t_0\)ならば\(S(t)(x_0,y_0) \in B_1\)」なので、\(B_1\)は吸収集合と言えました。

\(B_2 = \{(x_0,y_0) \mid (x_0 -1)^2+(y_0-1)^2 \leq 1\}\)はどうでしょうか？　時間経過したら原点に近づき、\(B_2\)からはみ出そうですね。

実際、吸収集合ではありません。たとえば、\((1,1)\)という初期値に注目します。\(\lim_{t\to \infty}S(t) (x_0,y_0)=(0,0)\)より、「\(t \geq T\)ならば\(x(t)^2 +y(t)^2\leq \frac{1}{4}\)」を満たす\(T\)が存在します。したがって、どんな\(t_0\)に対しても、\(S(t)(x_0,y_0) \not \in B_2\)を満たす\(t \geq t_0\)が存在すること、吸収集合でないことが言えました。

この例を考えると、原点とその付近を含まなければ、吸収集合にならないことがわかりますね。

散逸系とは

微分方程式によっては、「小さな」吸収集合が、あったりなかったりします。

力学系\((H,(S(t))_{t \geq 0})\)が散逸的（dissipative）とは、そこにコンパクトな吸収集合が存在することです。

ユークリッド空間\(\mathbb{R}^N\)においては、コンパクト集合とは有界な閉集合と同値です。

コンパクトという条件をつけるのは、もしコンパクトという条件をつけなければ、相空間全体\(B=H\)が常に吸収集合の定義を満たすからです。全体ではなく一部分が吸収しているような系を、散逸系と呼びます。

さきほどの常微分方程式

\[ \begin{aligned} \left\{ \begin{array}{l} \frac{dx}{dt} =-x+y \\ \frac{dy}{dt} =-x-y \end{array} \right.\end{aligned} \]

が定める力学系\((\mathbb{R}^2, (S(t)))\)は散逸的です。

なぜなら、吸収集合\(B_1 =\{(x_0,y_0)\mid x_0 ^2+y_0^2 \leq 1\}\)は、有界な閉集合なので。

別の例として、次の常微分方程式が定める力学系を考えましょう。

\[ \begin{aligned} \left\{ \begin{array}{l} \frac{dx}{dt} =y \\ \frac{dy}{dt} =-x \end{array} \right.\end{aligned} \]

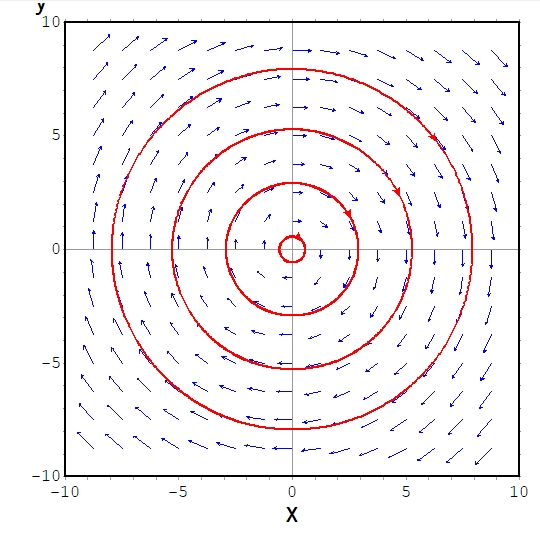
これは散逸系ではありません。

仮にコンパクトな吸収集合\(B\)が存在したとしましょう。\(B\)は有界なので、半径\(R\)の原点を中心とする円盤に含まれます。

その外側の点として、\((R+1,0)\)について考えましょう。それを初期値とする方程式の解は、\(S(t)(R+1,0)=((R+1)\cos t ,-(R+1)\sin t)\)です。上で示した図のように円周上を常にとどまり、すべての\(t\)に対して、\(\| ((R+1)\cos t ,-(R+1)\sin t)\|_{\mathbb{R}^2}= R+1\)です。よって、半径\(R\)の円盤に含まれず、常に\(S(t)(R+1,0) \not \in B\)となります。これは\(B\)が吸収集合であることに矛盾していますね。

今回は常微分方程式の例を紹介しましたが、熱方程式や反応拡散方程式、平面のナビエ・ストークス方程式などの偏微分方程式も、散逸系となることが知られています。

以上、吸収集合、散逸系とは：線形力学系を例に紹介してきました。

具体例を考える上では、線形常微分方程式の力学系だとイメージがしやすいですね。

吸収集合や散逸系の考え方は、アトラクターの議論に役立つでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。